数据结构8:栈

简介

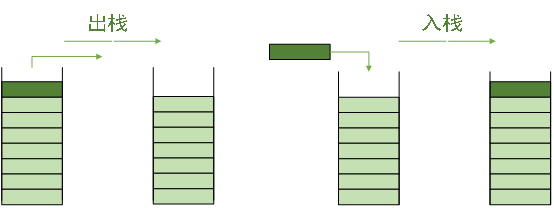
栈是一种类似于枪弹夹一样的数据结构，先进入的最后弹出，后进入的先弹出，如图1所示。栈栈分为栈顶和栈底，栈只允许对栈顶进行操作，从而决定了栈是先进后出的数据结构。

入栈：向栈中添加元素的操作叫做入栈或者压栈，如图2所示。

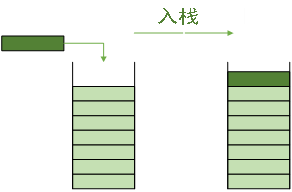
出栈：从栈中取出元素的操作叫做出栈或者弹栈，如图3所示。

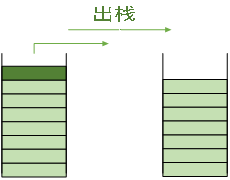
栈的数据结构和API函数：

我们教程中的栈是以线性表为基础实现的，因此栈的数据结构与线性表是一样的，栈的API也是在线性表的基础上实现的。简单的说，栈就是只允许在最前端操作的线性表，只需要在最前端插入元素和取出元素。为了简单方便，我们以单向链表为基础实现栈及其API函数。

栈的数据结构

//将线性表的数据结构定义为栈

typedef  List Stack;

栈的API函数

栈生成函数：

Stack *StackCreate()
{//定义一个Stack类型的指针Stack *temp = NULL;//利用ListCreate给分配栈空间temp = (Stack *)ListCreate();//返回栈指针return temp;
}

应用代码

Stack *mystack = NULL;
//建立一个栈
mystack = StackCreate();

栈销毁函数：

int StackDestroy(Stack **stack)
{int ret;//利用ListDestory销毁Stackret = ListDestory(stack);//返回操作的结果return ret;
}

应用代码：

StackDestroy(&mystack);

栈清空函数：

int StackClear(Stack *stack)
{int ret;//利用ListClear清空Stackret = ListClear(stack);//返回操作的结果return ret;
}

应用代码：

StackClear(&mystack);

栈长度获取函数：

int StackGetlen(Stack *stack)
{int ret;//利用ListGetLength获取栈长度ret = ListGetLength(stack);//返回栈的长度return ret;
}

应用代码：

len = StackGetlen(mystack);

栈空检测函数：

int StackEmpty(Stack *stack)
{int len;//获取栈的长度len = StackGetlen(stack);//如果长度为0，说明栈为空，返回1if (len==0){return 1;}return 0;
}

应用代码：

printf("StackEmpty:%d\n", StackEmpty(mystack));

栈满检测函数：

int StackFull(Stack *stack)
{int len;len = StackGetlen(stack);if (len == xx){return 1;}return 0;
}

占满函数与栈空函数类似，也是根据长度来判断的，因为我们使用的线性表是单向链表，元素可以动态地增加，因此无法判断其何时为满；当采用的线性表为顺序表时，该函数才有意义；也可以自己设定一个最大长度，当栈内元素等于该值时，无法插入元素，从而实现栈满，本文对此不做过多阐述。

元素入栈函数：

int StackPush(Stack *stack, int data)
{int ret;//利用ListAdd在栈首部插入元素ret =ListAdd(stack,0,data);//返回操作的结果return ret ;
}

应用代码：

for (i = 0; i < 5;i++)
{StackPush(mystack,i);
}

元素出栈函数：

int StackPop(Stack *stack)
{int ret;int data;//利用ListDelete在栈首部取出元素ret = ListDelete(stack,0,&data);//如果操作无误，返回数据，否则返回-1if (ret == 0){return data;}return -1;
}

应用代码：

for (i = 0; i < 5; i++)
{printf("%d:%d\n", i, StackPop(mystack));
}