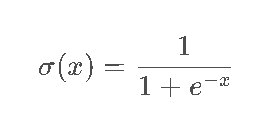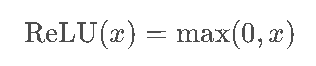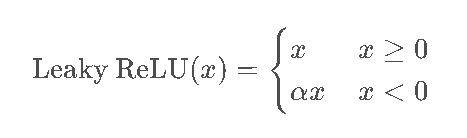当前位置：首页 > news >正文

激活函数只是“非线性开关“？ReLU、Sigmoid、Leaky ReLU的区别与选择

news 2025/10/21 10:38:37

一、激活函数：神经网络的"动力引擎"，而非简单开关

1.1 为什么必须用激活函数？

1.2 激活函数的三大核心作用

二、经典激活函数拆解：Sigmoid、ReLU、Leaky ReLU

2.1 Sigmoid："经典但危险"的概率开关

数学表达式

特性与痛点

2.2 ReLU："深度网络的救星"，但并非完美

数学表达式

特性与优势

致命缺陷：死亡ReLU问题

2.3 Leaky ReLU："改进版ReLU"，专治死亡问题

数学表达式

核心改进

变体与优化

三、三大激活函数对比：如何选择？

3.1 选择策略：按场景对号入座

任务类型：

网络深度：

数据分布：

四、代码实战：在PyTorch中体验激活函数

4.1 实验设置

4.2 代码实现

4.3 结果分析

五、总结：激活函数选择的"黄金法则"

在深度学习的神经网络中，激活函数是最容易被忽视却至关重要的组件之一。新手常误以为它只是"给线性变换加个非线性开关"，但实际它的作用远不止于此——它决定了信息如何在神经元之间传递，甚至直接影响模型的训练效率和最终效果。

本文将从激活函数的底层逻辑出发，拆解Sigmoid、ReLU、Leaky ReLU三大经典激活函数的数学本质、工程特性，并结合实际场景给出选择指南，帮你彻底跳出"开关论"的误区。

一、激活函数：神经网络的"动力引擎"，而非简单开关

1.1 为什么必须用激活函数？

假设神经网络没有激活函数（或仅用线性激活函数），那么无论叠加多少层，整个网络仍等价于一个单层线性模型。因为线性变换的组合仍是线性的（例如： y = W3*(W2*(W1*x + b1) + b2) + b3 = (W3W2W1)x + (W3W2b1 + W3b2 + b3) ）。

而现实中的数据（如图像、文本、语音）是非线性的——猫的轮廓不是直线，语音的频率变化不是简单叠加。激活函数通过引入非线性，让神经网络具备了"拟合任意复杂函数"的能力（数学上，通用近似定理证明了这一点）。

1.2 激活函数的三大核心作用

激活函数的价值远不止"非线性"：

控制输出范围：例如Sigmoid将输出压缩到(0,1)，适合概率预测；
调节梯度传播：ReLU的"单侧导数"特性可缓解梯度消失；
引入稀疏性：ReLU在输入为负时输出0，让部分神经元"关闭"，减少过拟合风险。

二、经典激活函数拆解：Sigmoid、ReLU、Leaky ReLU

2.1 Sigmoid："经典但危险"的概率开关

数学表达式及图像

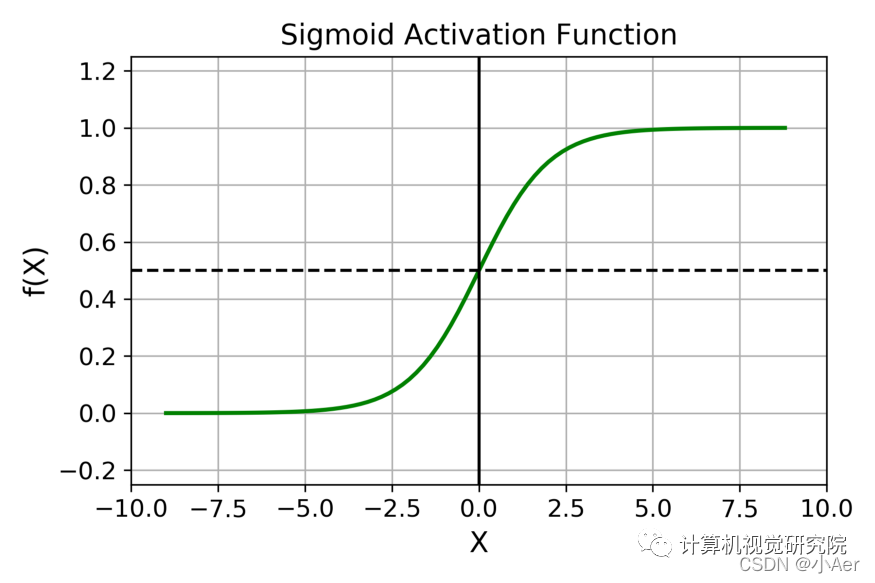
特性与痛点

输出范围有限：无论输入多大，输出始终在(0,1)之间，适合表示概率（如二分类任务的输出层）。
非线性饱和性：当输入绝对值很大时（如x>5或x<-5），Sigmoid的输出趋近于1或0，此时梯度几乎为0（导数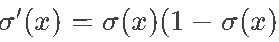，饱和时导数≈0）。
历史地位：早期神经网络（如2010年前）的"标配"，但因梯度消失问题，在深层网络中逐渐被ReLU取代。
典型场景：
- 二分类任务的输出层（配合交叉熵损失函数）；
- 需要概率解释的场景（如逻辑回归）。

2.2 ReLU："深度网络的救星"，但并非完美

数学表达式及图像

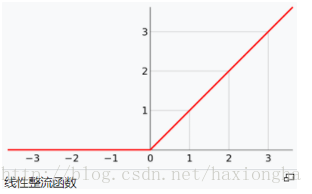
特性与优势

稀疏激活：输入为负时输出0，让部分神经元"关闭"，减少冗余计算（实验表明，ReLU网络比Sigmoid网络快6倍）；
梯度友好：输入为正时，梯度恒为1（无饱和问题），避免了深层网络的梯度消失；
生物合理性：更接近生物神经元的"全有或全无"特性（传统Sigmoid的平滑激活反而不太符合）。

致命缺陷：死亡ReLU问题

当输入长期为负时（如初始化权重过大、学习率过高），ReLU的输出会永久保持0，对应的神经元再也无法被激活（梯度永远为0）。这种现象称为"死亡ReLU"（Dying ReLU），会导致模型性能下降。

2.3 Leaky ReLU："改进版ReLU"，专治死亡问题

数学表达式及图像

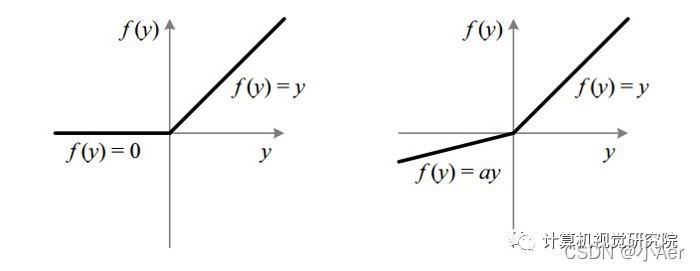
（公式为：Leaky ReLU(x) = { x (x≥0) ; αx (x<0) }，其中α是一个很小的正数，通常取0.01）

核心改进

针对ReLU的"死亡问题"，Leaky ReLU允许输入为负时保留一个小的梯度（α），避免神经元永久失效。例如，当α=0.01时，输入-1的输出是-0.01，梯度为0.01（而非0）。

变体与优化

PReLU（Parametric ReLU）：将α作为可学习的参数（而非固定值），模型训练时会自动调整α的大小；
ELU（Exponential Linear Unit）：用指数函数替代线性项（x<0时输出α(e^x -1)），更平滑地处理负区间，但计算成本略高。

三、三大激活函数对比：如何选择？

激活函数	数学表达式	输出范围	梯度特性	优点	缺点	典型场景
Sigmoid	1/(1+e^(-x))	(0,1)	输入绝对值大时梯度趋近0	输出归一化，概率解释性好	深层网络易梯度消失	二分类输出层
ReLU	max(0,x)	[0, +∞)	输入正梯度1，负梯度0	稀疏激活、无梯度消失	易死亡ReLU	隐藏层（深层网络）
Leaky ReLU	max(αx,x) (α≈0.01)	(-∞, +∞)	负区间保留小梯度	缓解死亡ReLU	α需人工设定	隐藏层（需避免神经元死亡）

3.1 选择策略：按场景对号入座

任务类型：

分类任务输出层：二分类用Sigmoid，多分类用Softmax（本质是Sigmoid的多类扩展）；
回归任务输出层：用线性激活函数（即f(x)=x）。

网络深度：

浅层网络（如LeNet-5）：Sigmoid仍可使用（但需注意初始化和学习率）；
深层网络（如ResNet-50）：优先选ReLU或其变体（Leaky ReLU/PReLU），避免梯度消失。

数据分布：

若数据中存在大量负样本（如医学影像中的"无病灶区域"），Leaky ReLU比ReLU更友好；
若模型训练中出现大量神经元死亡（可通过监控激活值为0的比例判断），尝试PReLU或增大α。

四、代码实战：在PyTorch中体验激活函数

4.1 实验设置

任务：二分类（用随机生成的非线性数据）；
网络结构：输入层（2节点）→ 隐藏层（16节点）→ 输出层（1节点）；
激活函数：分别测试Sigmoid、ReLU、Leaky ReLU；
损失函数：二元交叉熵（BCELoss）；
优化器：Adam（学习率0.01）。

4.2 代码实现

import torch  
import torch.nn as nn  
import matplotlib.pyplot as plt  # 生成非线性数据（类似异或问题）  
torch.manual_seed(42)  
X = torch.randn(1000, 2)  
y = (X[:,0]**2 + X[:,1]**2 > 1).float().unsqueeze(1)  # 圆外为1，圆内为0  # 定义带不同激活函数的模型  
class Net(nn.Module):  def __init__(self, activation):  super().__init__()  self.layers = nn.Sequential(  nn.Linear(2, 16),  activation,  # 激活函数可替换  nn.Linear(16, 1),  nn.Sigmoid()  # 输出层用Sigmoid  )  def forward(self, x):  return self.layers(x)  # 训练函数  
def train(activation, epochs=100):  model = Net(activation)  criterion = nn.BCELoss()  optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  losses = []  for epoch in range(epochs):  optimizer.zero_grad()  outputs = model(X)  loss = criterion(outputs, y)  loss.backward()  optimizer.step()  losses.append(loss.item())  return losses  # 测试三种激活函数  
sigmoid_losses = train(nn.Sigmoid())  
relu_losses = train(nn.ReLU())  
leaky_relu_losses = train(nn.LeakyReLU(0.01))  # 绘制损失曲线  
plt.plot(sigmoid_losses, label='Sigmoid')  
plt.plot(relu_losses, label='ReLU')  
plt.plot(leaky_relu_losses, label='Leaky ReLU')  
plt.xlabel('Epochs')  
plt.ylabel('Loss')  
plt.legend()  
plt.show()