动态规划之两个字符组/两个数组的dp问题

题目连接

1143. 最长公共子序列 - 力扣（LeetCode）

72. 编辑距离 - 力扣（LeetCode）

思路分析

这两道题有本质上就是一种类型的题，放在一起，便于帮助理解两个字符串的dp问题

最长公共子序列思路

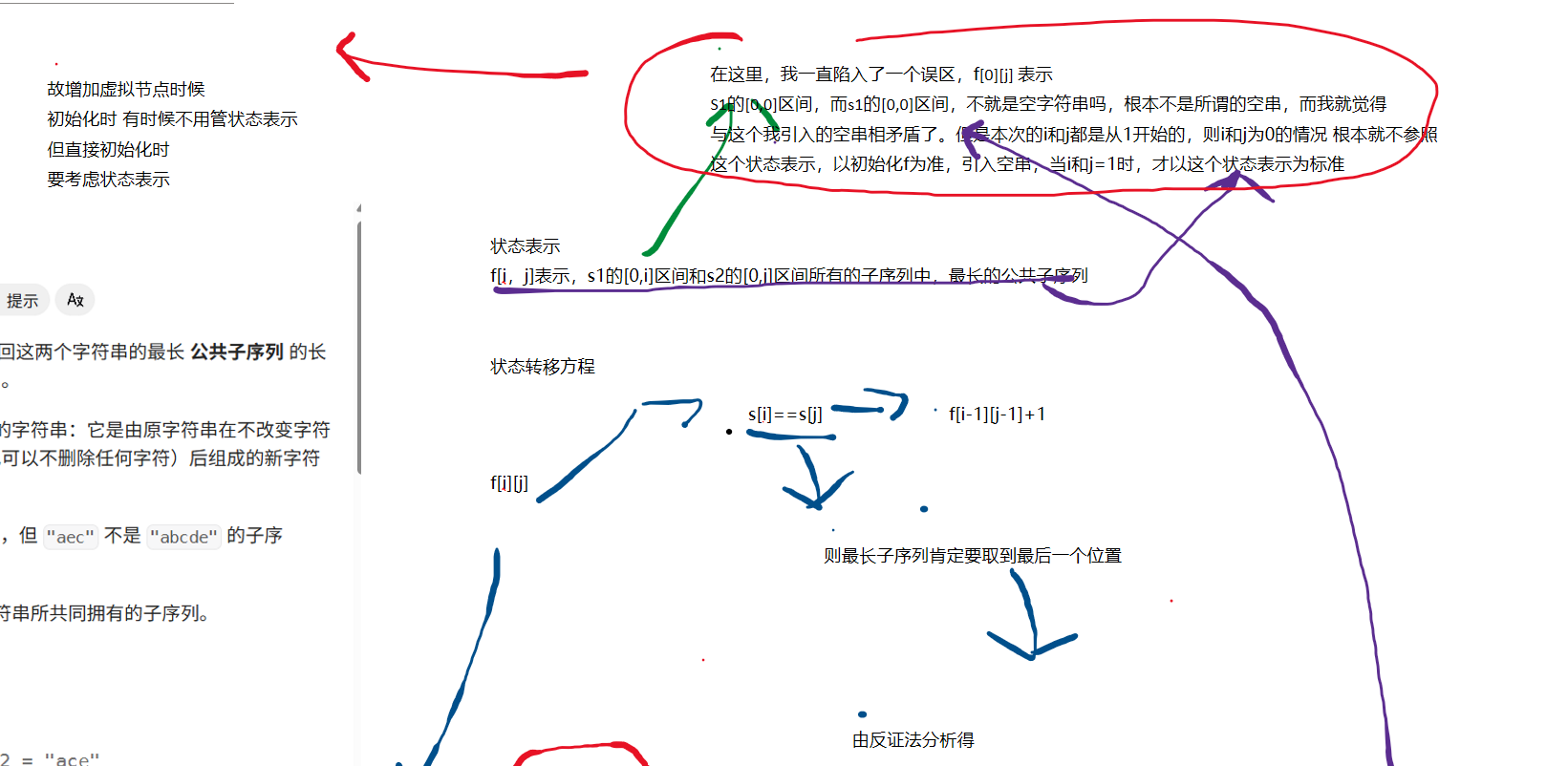
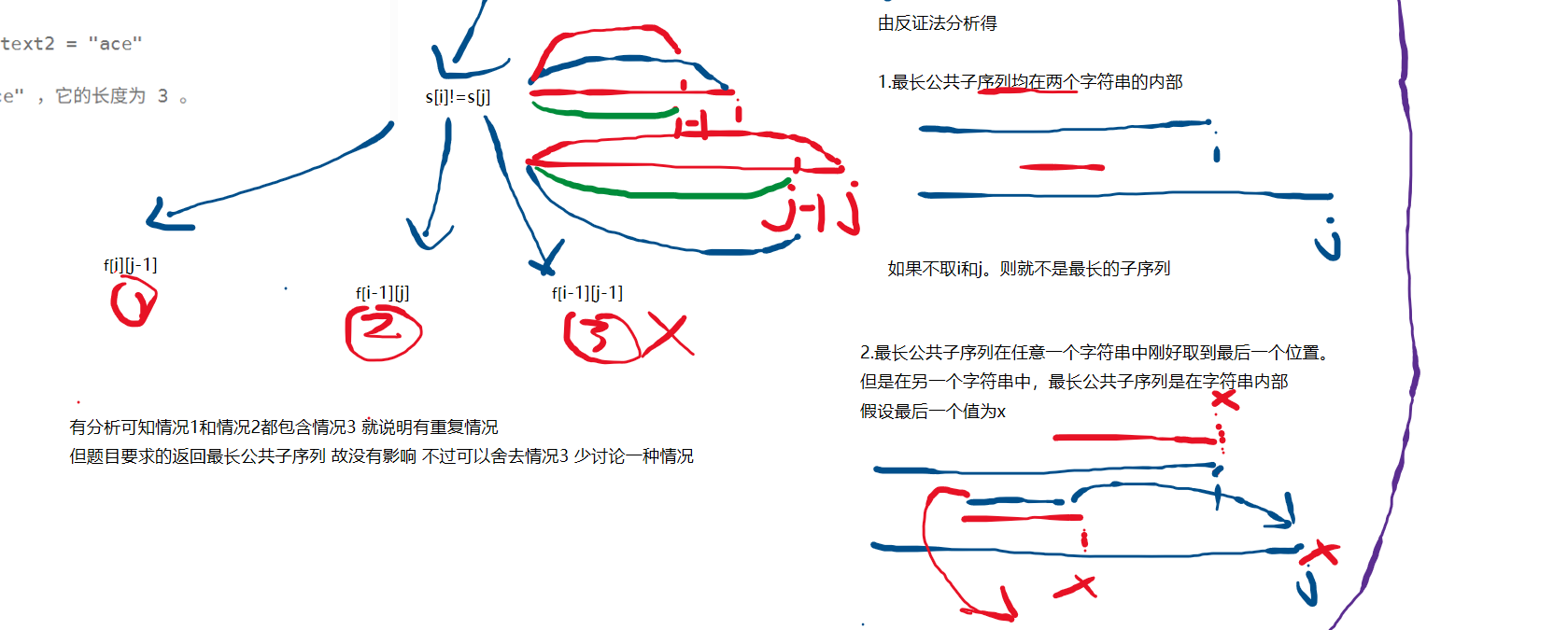
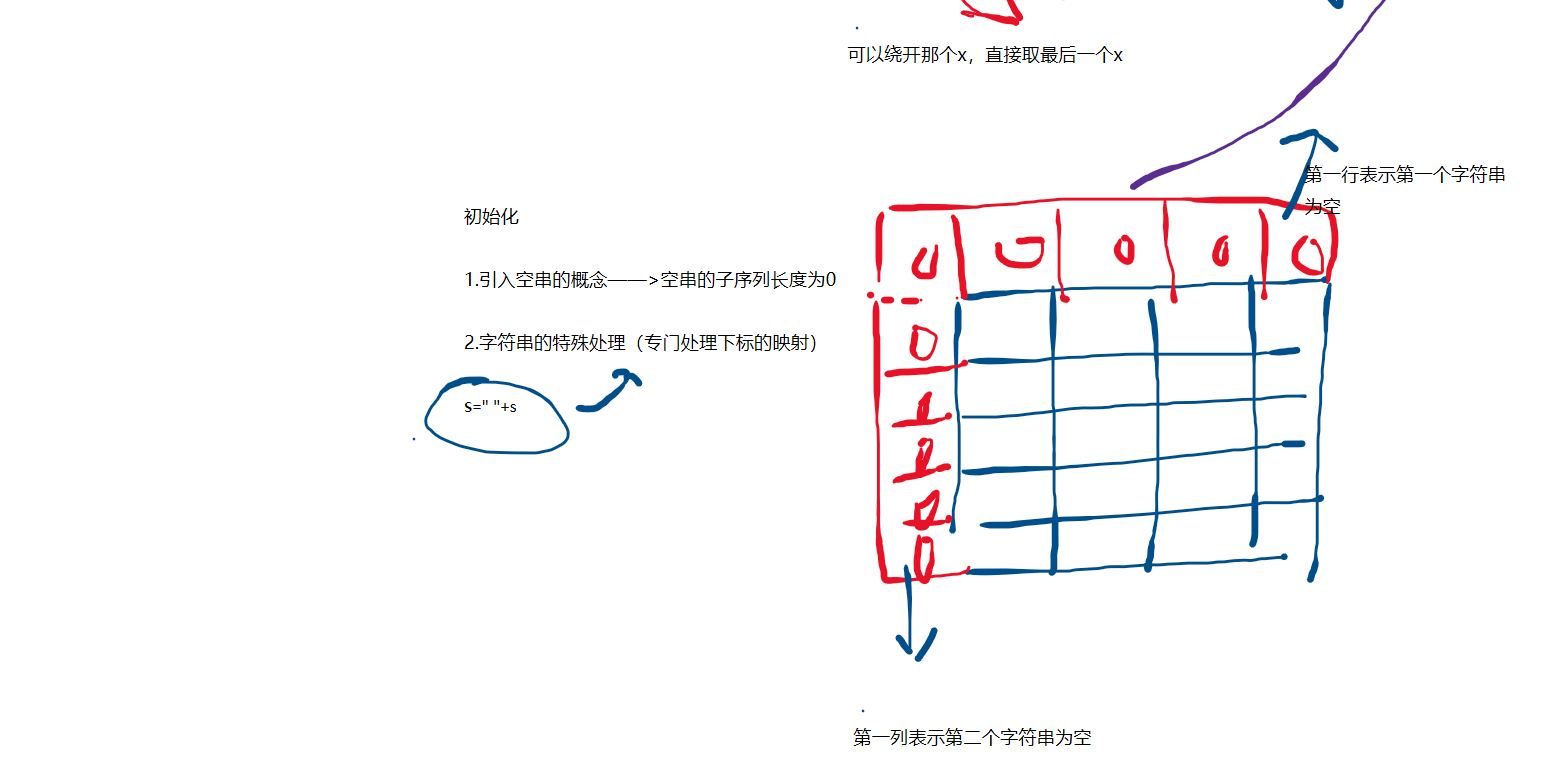
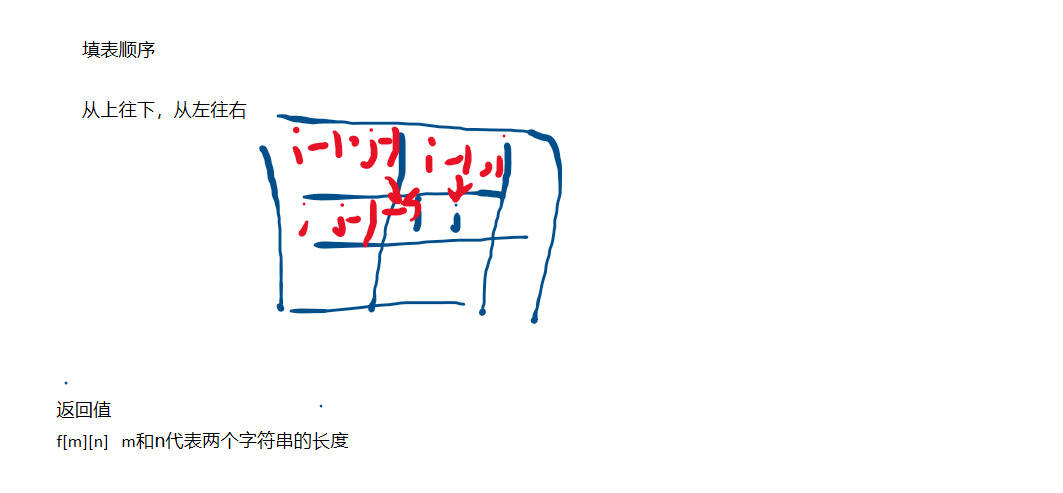
代码实现

class Solution {public int longestCommonSubsequence(String text1, String text2) {int m=text1.length();int n=text2.length();int[][] f=new int[m+1][n+1];text1=" "+text1;text2=" "+text2;for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){char first=text1.charAt(i);char second=text2.charAt(j);if(first==second){f[i][j]=f[i-1][j-1]+1;}else{f[i][j]=Math.max(f[i][j-1],f[i-1][j]);}}}return f[m][n];}
}

编辑距离思路

这个重点理解哦 插入和删除本质上是一样的

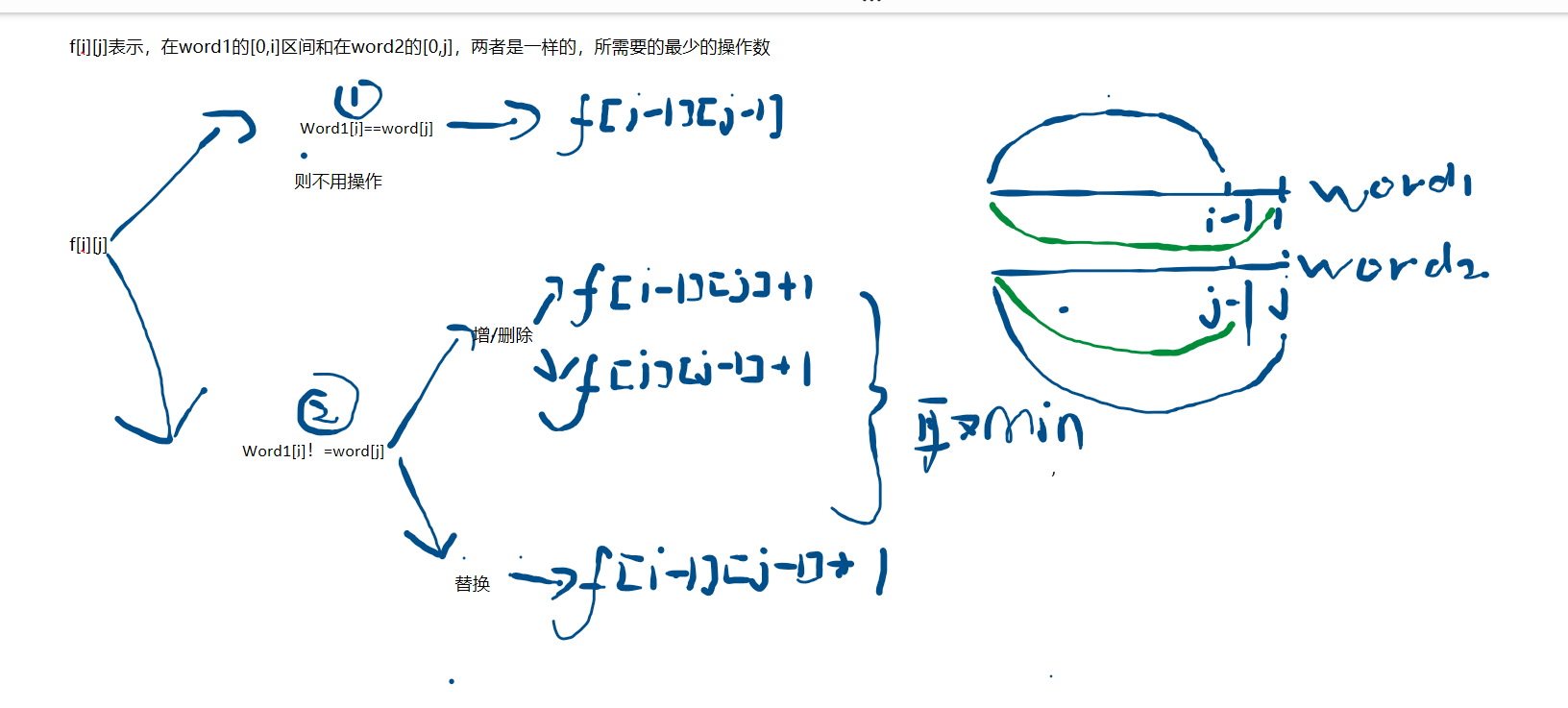
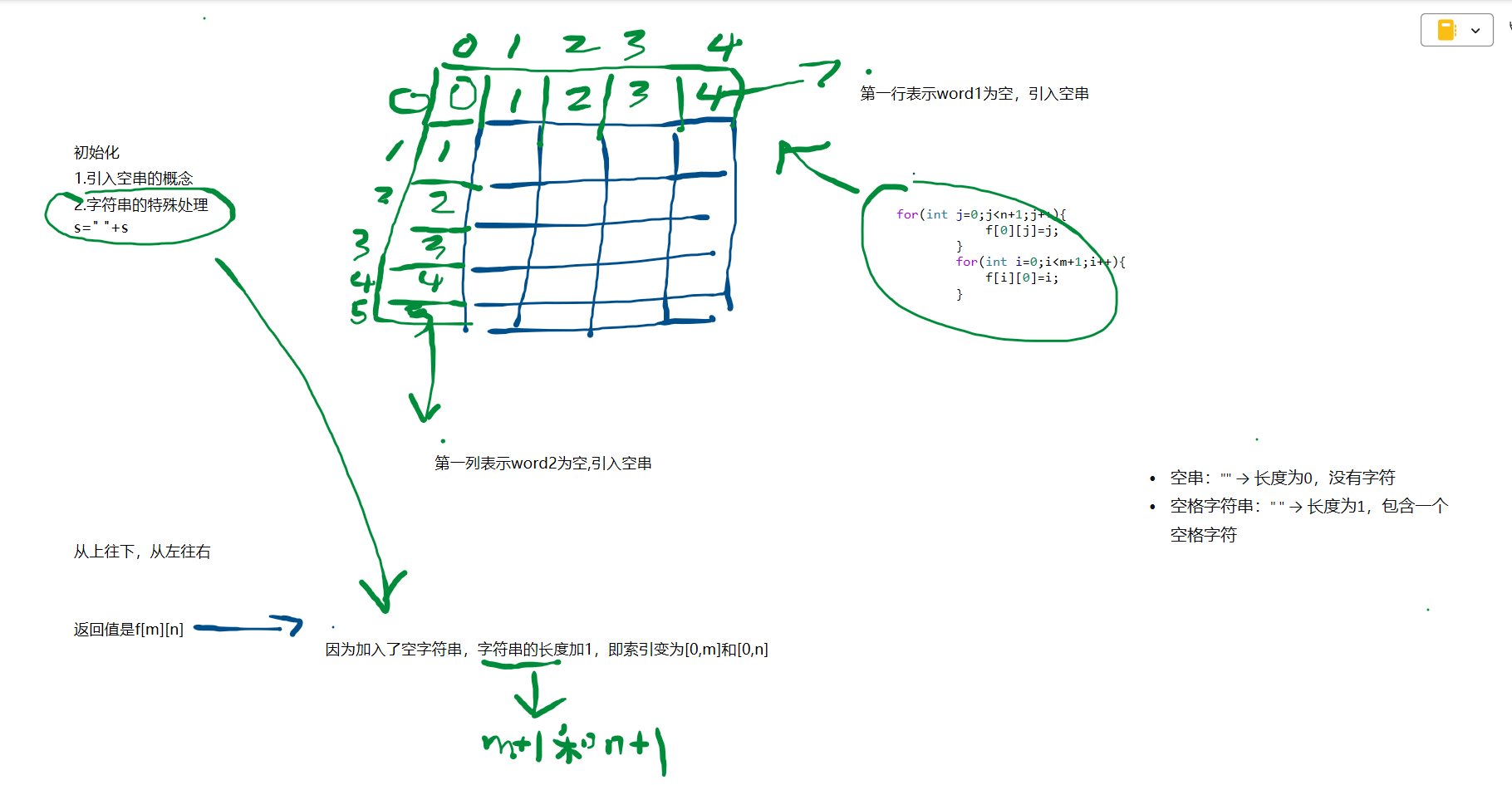
代码实现

class Solution {public int minDistance(String word1, String word2) {int m=word1.length();int n=word2.length();int[][] f=new int[m+1][n+1];for(int j=0;j<n+1;j++){f[0][j]=j;}for(int i=0;i<m+1;i++){f[i][0]=i;}word1=" "+word1;word2=" "+word2;for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){if(word1.charAt(i)==word2.charAt(j)){f[i][j]=f[i-1][j-1];}else{f[i][j]=Math.min(f[i-1][j-1]+1,Math.min(f[i-1][j]+1,f[i][j-1]+1));}}}return f[m][n];    }
}