机器学习(4)多特征与向量化
一、多特征(Multiple Features)
1. 特征与特征数量
在现实问题中,一个样本往往不止一个特征(feature)。例如,在预测房价问题中,影响价格的因素可能有:
| 特征编号 | 特征名称 | 符号表示 | 含义 |
|---|---|---|---|
| 1 | 房屋面积 | x1 | 面积越大,房价越高 |
| 2 | 房间数量 | x2 | 房间越多,价格越高 |
| 3 | 房龄 | x3 | 越新越贵 |
对于第 i 个样本:
![]()
共有 n 个特征。
2. 多元线性回归模型(Multivariate Linear Regression)
单变量线性回归公式为:
![]()
扩展到多特征的情形:
![]()
这就是多元线性回归模型。
3. 用房价预测举例
假设我们要预测房价:
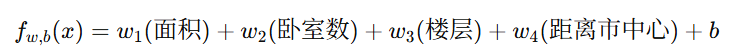
每个 wi 表示该特征对房价的影响程度。
4. 向量化表示(Vector Form)
将所有特征合并为一个向量:
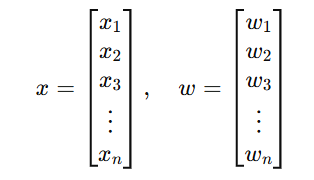
于是可以写成向量形式:
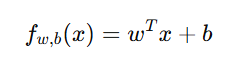
其中 wTx 表示向量点积(dot product)。
二、向量化(Vectorization)
1. 向量化的含义
向量化是指将循环计算改写成矩阵或向量运算,以便让计算机(尤其是 NumPy、GPU)利用底层并行加速。
在多特征线性回归中:
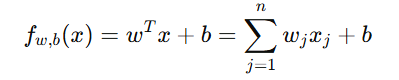
这就是点积(dot product)的数学表达式。
2. 点积的不同实现方式
| 方法 | Python 实现 | 运行原理 |
|---|---|---|
| for 循环 | for j in range(n): f += w[j]*x[j] | 每次循环计算一个元素,逐步累加,串行执行 |
| NumPy 向量化 | f = np.dot(w, x) + b | 一次性进行全部计算,利用底层并行加速 |
因此,np.dot() 方式在计算速度上要比 for 循环高得多。
3. 向量化在梯度下降中的应用
在线性回归的梯度下降中,需要同时计算多个样本的预测结果。
如果使用 for 循环:
for i in range(m): f_wb_i = np.dot(w, x[i]) + b
如果使用向量化:
f_wb = np.dot(X, w) + b
其中:
X 是一个 m×n 的矩阵(m个样本、n个特征)
计算结果 fwb 是一个 m×1 的预测向量
这样可以同时计算所有样本的预测值,大大提升效率。
三、多元线性回归的比较与优化
1. 模型、代价函数、梯度下降的对比
| 项目 | 单变量 | 多变量(向量化后) |
|---|---|---|
| 模型 | ||
| 代价函数 | ||
| 梯度下降 | 手动循环更新 | 一次性矩阵运算,向量化更新 |
向量化能极大提升效率,尤其是在大样本与高维数据中。
2. 多特征下梯度下降公式
向量化梯度公式为:
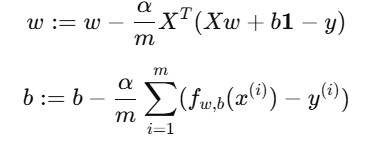
其中:
X:训练样本矩阵(形状 m×n)
y:目标向量(形状 m×1)
1:全1向量,用于加上偏置项 b
3. 正规方程(Normal Equation)法
在样本规模较小的情况下,可以直接使用正规方程求出最优解,无需迭代梯度下降。
公式如下:
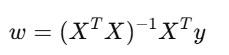
并且:
![]()
该方法通过线性代数的方式直接计算最优参数。
注意:
当特征数量非常多时(如上千维),计算的代价会非常高,此时仍推荐使用 梯度下降(Gradient Descent)。
四、 小结(Summary)
| 内容 | 单变量线性回归 | 多元线性回归(向量化) |
|---|---|---|
| 模型 | ||
| 输入 | 单个特征 x | 多个特征向量 x=[x1,x2,...,xn] |
| 计算方式 | 手动循环 | 矩阵向量化 |
| 优化方法 | 梯度下降 | 向量化梯度下降 / 正规方程 |
| 优点 | 简单直观 | 高效并行、便于扩展 |
