当前位置：首页 > news >正文

构建AI智能体：六十九、Bootstrap采样在大模型评估中的应用：从置信区间到模型稳定性

news 2025/10/21 8:06:22

一. 引言

在我们选择使用一个模型时，我们经常需要评估模型的性能。通常，我们会将数据集分为训练集和测试集，用测试集来评估模型的泛化能力。然而，单次划分的测试集可能不能完全代表模型在未知数据上的表现，特别是当数据集较小的时候。Bootstrap采样是一种强大的统计方法，可以通过重采样来估计统计量的分布，从而更稳健地评估模型性能，其基本思想是通过从原始数据集中随机抽取n个样本（允许重复抽取）形成一个新的数据集，称为Bootstrap样本，然后，我们可以基于这些Bootstrap样本计算统计量（如均值、标准差等）的分布。

同时，随着大模型（如深度神经网络）的兴起，模型的不确定性评估和性能稳健性变得尤为重要。Bootstrap采样可以与大模型结合，用于计算模型性能的置信区间、模型集成等，从而提供更可靠的模型评估。

本文将从Bootstrap采样的基本概念入手，由浅入深地介绍如何将Bootstrap采样与大模型结合使用，并通过一个具体的代码示例展示实际应用。

一、什么是Bootstrap采样

Bootstrap采样是一种统计学方法，它的核心思想是“以小见大，通过模拟逼近真实”，即在只有一份样本的情况下，通过对原始数据集进行有放回的随机抽样，这个过程重复多次，从而得到多个Bootstrap样本。然后，我们可以基于这些Bootstrap样本估计统计量（如均值、方差、中位数等）的抽样分布。这种方法特别适用于小样本数据集，能够有效估计统计量的分布和不确定性。

Bootstrap采样的步骤：

1. 从原始数据集中随机抽取一个样本，并记录。
2. 将该样本放回原始数据集，使得下次抽样时该样本仍有可能被抽到。
3. 重复步骤1和2，直到抽取的样本数量达到原始数据集的样本数n。这样就得到了一个Bootstrap样本。
4. 重复上述过程B次（例如B=1000），得到B个Bootstrap样本。

每个Bootstrap样本与原始数据集的大小相同，但由于是有放回抽样，每个Bootstrap样本中有些样本会出现多次，而有些样本则不会出现。

通俗的解释：

想象一下，我们有一个装有 N 个球的袋子（总体），但我们不能看到里面所有的球，只被允许伸手进去随机抓取一次，得到了一个包含 n 个球的样本。现在，我们想知道抓到的这些球的平均重量（样本均值）离所有球的真实平均重量（总体均值）有多远。

传统方法需要知道总体的分布或者依靠一些其他方式。但 Bootstrap 提供了一个巧妙的思路：

把整个袋子的球当作原始样本看作是一个总体，然后我们从这个总体中，进行有放回地随机抽样
每次也抽取 n 个球，由于是有放回的，我们抽到的球可能有些是重复的，有些则没被抽到；
这样重复这个过程成百上千次，我们就得到了很多个新样本（Bootstrap 样本）；
通过计算每个新样本的统计量（如均值），我们就可以构建出这个统计量的一个经验分布；
这个分布就近似于该统计量在真实总体中的抽样分布，我们可以用这个分布来计算标准误、置信区间等。

具体采样操作过程：

假设装有个N个球的袋子是一个原始数据集，比如原始数据 = [数据1, 数据2, 数据3, ..., 数据n]，里面包含了 n 个数据点。接下来我们去了解从这个数据计算出的某个统计量（比如平均值）的可靠程度。

第一步：准备我们的“总体”

把手中唯一的这个原始样本，想象成它就是整个总体，这是所有工作的基础。

第二步：有放回地抽取一个新样本

从这个“总体”即这份原始样本中，进行有放回的随机抽样。
具体操作：像抽奖一样，从原始数据中随机抓取一个数据，记录下它，然后把它放回去。再随机抓取一个，记录，再放回... 如此重复 n 次。
这样我们就得到了第一个 Bootstrap 样本。
重要特征：由于是放回的，这个新样本里，有些原始数据会被抽到多次，有些则一次也抽不到。

第三步：计算新样本的统计量

对刚生成的这个 Bootstrap 样本，计算我们关心的那个统计量，比如计算它的平均值。我们把这个计算出的值记作 Bootstrap平均值1。

第四步：重复上述过程成百上千次

将第二步和第三步重复执行很多次，比如 B = 1000 次。
这样我们就会得到 1000 个 Bootstrap 样本，并对应计算出 1000 个 Bootstrap 统计量（例如：[Bootstrap平均值1, Bootstrap平均值2, ..., Bootstrap平均值1000]）。

第五步：利用这堆“副本”统计量进行分析

现在我们拥有了 1000 个统计量（例如 1000 个平均值），它们形成了一个分布，我们称之为 Bootstrap 分布。这个分布可以用来估计真实世界中的抽样 variability（波动性）。
估计标准误（波动大小）：
- 直接计算这 1000 个 Bootstrap 平均值的标准差。这个标准差就是原始样本平均值的标准误的一个很好的估计。
- 标准误的估计值 = 所有Bootstrap平均值的标准差
构建置信区间（一个可能的值范围）：
- 一个非常简单的方法是使用百分位数法。
- 将刚才的 1000 个 Bootstrap 平均值从小到大排序。
- 找一个 95% 的置信区间：
  - 下限：排在第 25 位（1000 * 2.5%）的那个值。
  - 上限：排在第 975 位（1000 * 97.5%）的那个值。
- 这两个值就构成了平均值的一个 95% 置信区间。

用一个数组示例来执行以上步骤：

原始数据：[3, 5, 7, 9, 11] (n=5)
原始平均值：(3+5+7+9+11)/5 = 7

1. 第一次Bootstrap抽样：可能抽到 [5, 7, 3, 9, 5]

计算 Bootstrap平均值1：(5+7+3+9+5)/5 = 5.8

2. 第二次Bootstrap抽样：可能抽到 [11, 3, 7, 7, 9]

计算 Bootstrap平均值2：(11+3+7+7+9)/5 = 7.4

3. 第三次Bootstrap抽样：可能抽到 [9, 11, 11, 3, 7]

计算 Bootstrap平均值3：(9+11+11+3+7)/5 = 8.2

... 重复直到1000次。

分析：

最后我们得到了一个包含 1000 个数字的列表：[5.8, 7.4, 8.2, ...]。
计算这个列表的标准差，假设是 1.2，那么我们就可以说，原始平均值 7 的标准误大约为 1.2。
将这个列表排序后，找到第25个数（比如 4.5）和第975个数（比如 9.5），那么我们可以说“我们有95%的把握认为总体平均值在 4.5 到 9.5 之间”。

通过这种方式，Bootstrap 采样仅利用我们手头的一份样本，就通过自力更生的方式，模拟出了多次抽样实验，也让我们对Bootstrap 采样有了清晰的认识。

三、Bootstrap采样的优缺点

优点：

无需分布假设：不依赖于总体分布的具体形式，是一种非参数方法。
简单易行：只需原始样本，通过重采样即可实现。
适用于小样本：在小样本情况下，Bootstrap方法往往比传统方法更可靠。

缺点：

计算量大：需要生成大量Bootstrap样本并计算统计量，对计算资源要求较高。
对原始样本的依赖性：如果原始样本不能很好地代表总体，Bootstrap结果也会有偏差。
不适用于所有统计量：对于某些统计量（如极值），Bootstrap方法可能效果不佳。

四、Bootstrap在大模型的作用

不确定性量化：评估模型预测的置信度
模型稳定性：检测模型对数据扰动的敏感性
性能评估：更准确地估计模型泛化能力
集成学习：通过多个bootstrap样本训练多个模型，提升整体性能

五. Bootstrap的应用场景

Bootstrap 的应用极其广泛，包括但不限于：

估计标准误和置信区间：对于任何复杂的统计量（如中位数、相关系数、回归系数、机器学习模型的预测精度等）。
偏差估计：比较 Bootstrap 统计量的均值与原始统计量，可以估计统计量的偏差。
假设检验：通过 Bootstrap 方法模拟零假设下的数据分布，计算 p-value。
机器学习：著名的 Bagging算法就是基于 Bootstrap 采样来降低模型方差，例如随机森林。

六、Bootstrap采样分步计算示例

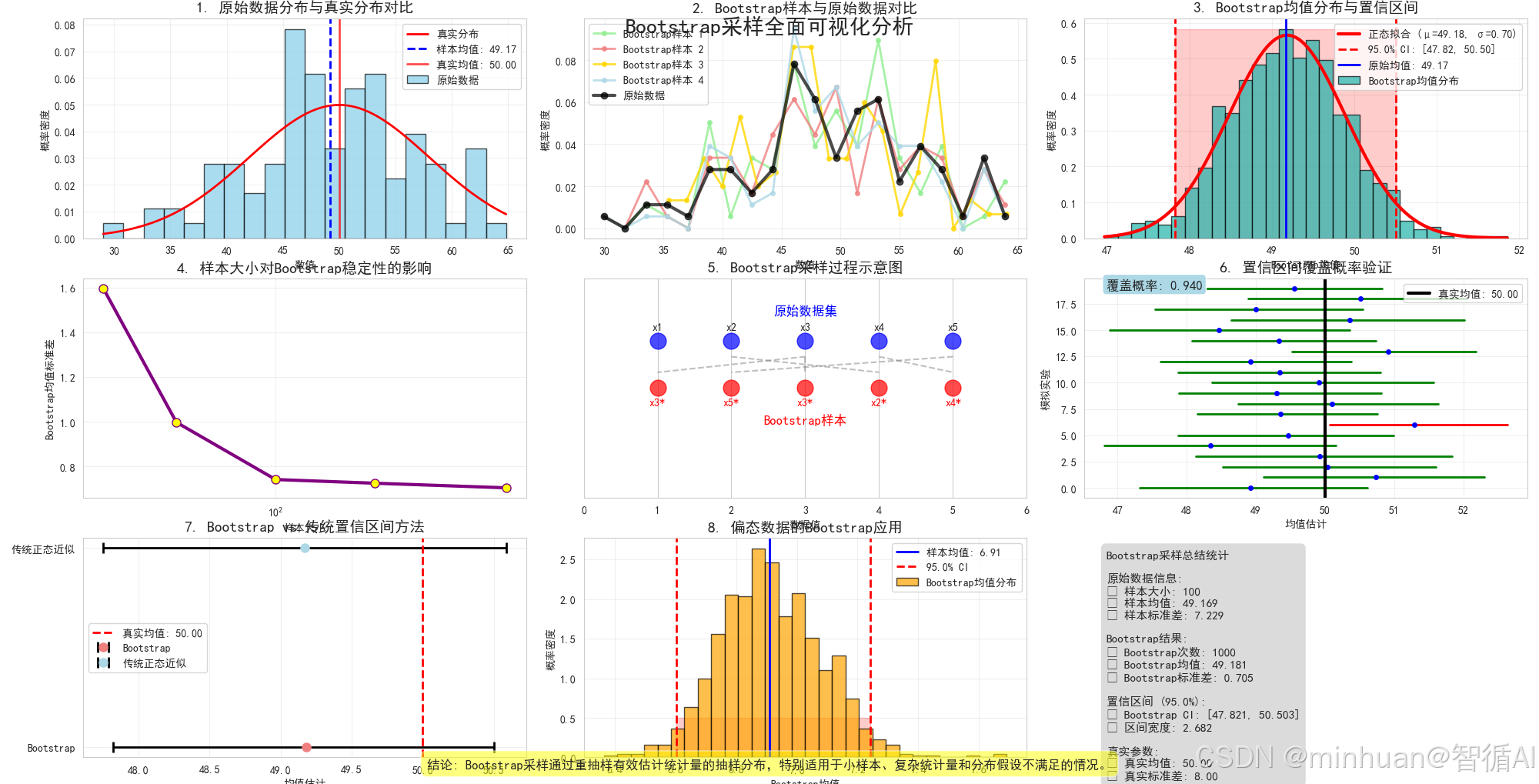
我们创建一个完整的Bootstrap采样示例，并可视化其过程。我们将使用一个简单的数据集，并展示Bootstrap采样的多个样本，以及如何用这些样本估计统计量的分布。

执行步骤：

1. 生成一个原始数据集（假设是从某个总体中抽取的样本）。
2. 进行Bootstrap采样（有放回抽样）生成多个Bootstrap样本。
3. 计算每个Bootstrap样本的统计量（例如均值、中位数等）。
4. 可视化原始数据、Bootstrap样本以及统计量的分布。

示例目的：

展示Bootstrap采样的过程。
展示如何通过Bootstrap样本来估计统计量的分布。
说明Bootstrap采样如何用于计算置信区间等。

1. 原始数据分布与真实分布对比

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import statsdef plot_original_vs_true_distribution():"""图1：原始数据分布与真实分布对比"""np.random.seed(42)# 参数设置true_mean = 50true_std = 8n_original = 100# 生成原始数据original_data = np.random.normal(true_mean, true_std, n_original)# 计算统计量original_mean = np.mean(original_data)original_std = np.std(original_data)original_se = original_std / np.sqrt(n_original)  # 标准误print("=== 计算内容 ===")print(f"真实总体参数: μ={true_mean}, σ={true_std}")print(f"样本统计量: 均值={original_mean:.3f}, 标准差={original_std:.3f}")print(f"标准误: {original_se:.3f}")print(f"抽样误差: {abs(original_mean - true_mean):.3f}")# 创建图表plt.figure(figsize=(10, 6))# 绘制原始数据直方图n_bins = 20counts, bins, patches = plt.hist(original_data, bins=n_bins, alpha=0.7, color='skyblue', edgecolor='black', label='原始样本数据', density=True)# 添加理论正态分布曲线x = np.linspace(original_data.min(), original_data.max(), 100)theoretical_pdf = stats.norm.pdf(x, true_mean, true_std)plt.plot(x, theoretical_pdf, 'r-', linewidth=2, label='真实总体分布')# 添加参考线plt.axvline(original_mean, color='blue', linestyle='--', linewidth=2, label=f'样本均值: {original_mean:.2f}')plt.axvline(true_mean, color='red', linestyle='-', linewidth=2, alpha=0.7, label=f'真实均值: {true_mean:.2f}')plt.xlabel('数值')plt.ylabel('概率密度')plt.title('图1: 原始数据分布与真实分布对比\n(展示抽样误差)', fontsize=14, fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)# 添加统计信息文本框textstr = '\n'.join([f'样本大小: n={n_original}',f'样本均值: {original_mean:.3f}',f'样本标准差: {original_std:.3f}',f'抽样误差: {abs(original_mean-true_mean):.3f}'])props = dict(boxstyle='round', facecolor='wheat', alpha=0.8)plt.text(0.02, 0.98, textstr, transform=plt.gca().transAxes, fontsize=10,verticalalignment='top', bbox=props)plt.tight_layout()plt.show()return original_data, original_mean, original_std# 运行图1
original_data, sample_mean, sample_std = plot_original_vs_true_distribution()

输出结果：

=== 计算内容 ===
真实总体参数: μ=50, σ=8
样本统计量: 均值=49.169, 标准差=7.229
标准误: 0.723
抽样误差: 0.831

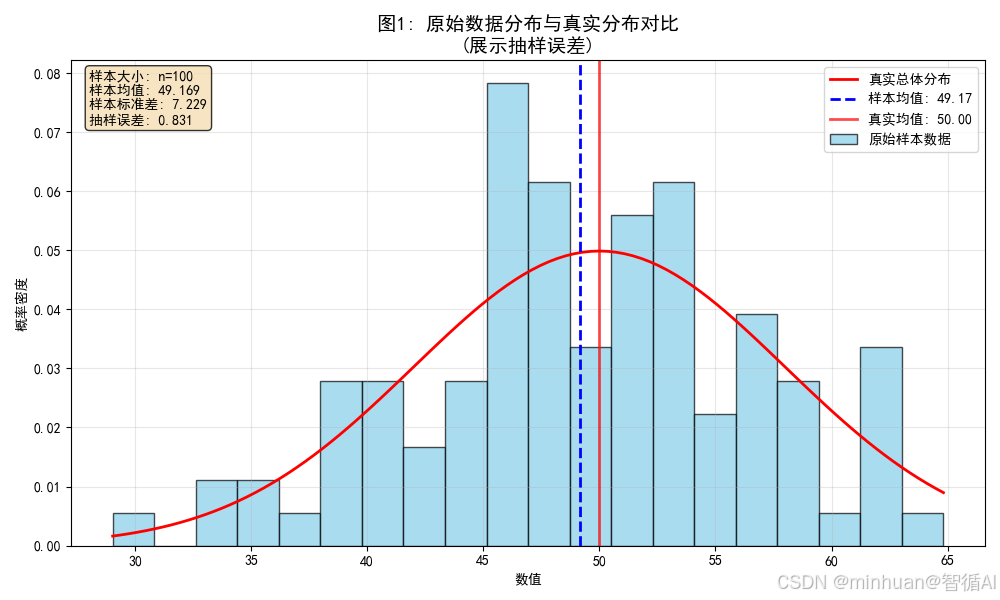
图示内容：显示原始样本数据的分布与真实总体分布的对比
图片含义：
- 蓝色直方图：从真实分布中抽取的100个样本
- 红色曲线：真实的正态分布N(50, 8)
- 蓝色虚线：样本均值
- 红色实线：真实均值
目的：展示样本数据与总体之间的关系，说明抽样误差的存在
效果：直观显示样本均值与真实均值的差异，体现抽样的随机性
计算内容说明：
- 真实总体参数：设定正态分布 N(50, 8) 作为数据生成过程
- 样本统计量：从总体中随机抽取100个样本，计算样本均值和标准差
- 标准误：公式（SE = σ / √n），衡量样本均值的抽样变异性
- 抽样误差：|样本均值 - 真实均值|，体现单次抽样的随机误差

扩展说明：标准误的公式解释

公式： SE = σ / √n
中文描述：标准误 = 总体标准差 / 样本量的平方根
各符号含义：
- SE：标准误
- σ：总体标准差
- n：样本量
- √：平方根符号

2. Bootstrap采样过程示意图

def plot_bootstrap_sampling_process():"""图2：Bootstrap采样过程示意图"""np.random.seed(123)# 创建小型示例数据集demo_data = np.array([10, 20, 30, 40, 50])data_labels = ['A', 'B', 'C', 'D', 'E']# 执行一次Bootstrap采样bootstrap_indices = np.random.choice(len(demo_data), size=len(demo_data), replace=True)bootstrap_sample = demo_data[bootstrap_indices]print("\n=== 计算内容 ===")print(f"原始数据集: {demo_data}")print(f"数据标签: {data_labels}")print(f"Bootstrap采样索引: {bootstrap_indices}")print(f"Bootstrap样本: {bootstrap_sample}")print(f"样本组成: {[data_labels[i] for i in bootstrap_indices]}")# 计算每个原始数据点在Bootstrap样本中出现的次数occurrence_count = {}for idx in bootstrap_indices:label = data_labels[idx]occurrence_count[label] = occurrence_count.get(label, 0) + 1print(f"数据点出现次数: {occurrence_count}")# 创建图表plt.figure(figsize=(12, 8))# 绘制原始数据集y_original = 6for i, (value, label) in enumerate(zip(demo_data, data_labels)):plt.plot(value, y_original, 'o', markersize=80, color='lightblue', alpha=0.8)plt.text(value, y_original, f'{label}\n{value}', ha='center', va='center', fontweight='bold', fontsize=12)# 绘制Bootstrap样本y_bootstrap = 2for i, (value, label) in enumerate(zip(bootstrap_sample, [data_labels[idx] for idx in bootstrap_indices])):plt.plot(value, y_bootstrap, 'o', markersize=80, color='lightcoral', alpha=0.8)plt.text(value, y_bootstrap, f'{label}*\n{value}', ha='center', va='center', fontweight='bold', fontsize=12)# 绘制采样连线for i, (orig_idx, bs_value) in enumerate(zip(bootstrap_indices, bootstrap_sample)):orig_x = demo_data[orig_idx]orig_y = y_original - 0.3bs_y = y_bootstrap + 0.3# 绘制箭头plt.annotate('', xy=(bs_value, bs_y), xytext=(orig_x, orig_y),arrowprops=dict(arrowstyle='->', color='gray', lw=1.5, alpha=0.6))plt.xlim(0, 60)plt.ylim(0, 7)plt.xlabel('数据值')plt.title('图2: Bootstrap采样过程示意图\n(有放回随机抽样)', fontsize=14, fontweight='bold')plt.gca().set_yticks([y_original, y_bootstrap])plt.gca().set_yticklabels(['原始数据集', 'Bootstrap样本'])plt.grid(True, alpha=0.3)# 添加说明文本explanation_text = ("Bootstrap采样过程:\n""1. 从原始数据集中有放回地随机抽取n个样本\n""2. 某些原始数据点可能被多次抽取\n""3. 某些原始数据点可能不被抽取\n"f"4. 本例中: {occurrence_count}")plt.text(0.02, 0.15, explanation_text, transform=plt.gca().transAxes, fontsize=10,bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8))plt.tight_layout()plt.show()return bootstrap_sample, occurrence_count# 运行图2
bootstrap_sample, occurrence_count = plot_bootstrap_sampling_process()

输出结果：

=== 计算内容 ===
原始数据集: [10 20 30 40 50]
数据标签: ['A', 'B', 'C', 'D', 'E']
Bootstrap采样索引: [2 4 2 1 3]
Bootstrap样本: [30 50 30 20 40]
样本组成: ['C', 'E', 'C', 'B', 'D']
数据点出现次数: {'C': 2, 'E': 1, 'B': 1, 'D': 1}

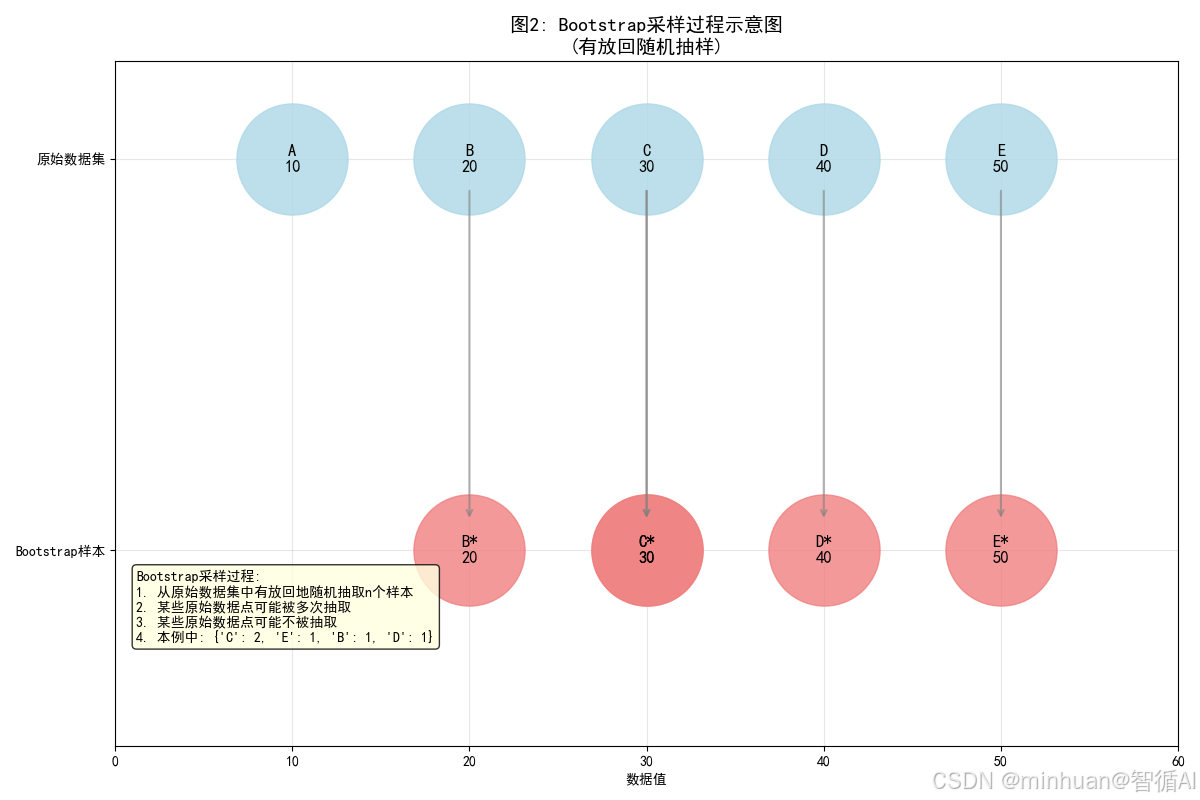
图示内容：Bootstrap采样的机制演示
图片含义：
- 上方蓝点：原始数据点
- 下方红点：Bootstrap样本点
- 灰色虚线：抽样关系
目的：用简单示例说明有放回抽样的过程
效果：清晰展示Bootstrap采样的核心机制
计算内容说明：
- 原始数据集：[A:10, B:20, C:30, D:40, E:50] 作为示例
- Bootstrap采样：有放回地随机抽取5个样本
- 采样结果分析：记录每个原始数据点在新样本中出现的次数
- 关键特性：展示Bootstrap采样的随机性和有放回特性

3. Bootstrap样本分布对比

def plot_bootstrap_samples_comparison(original_data, n_bootstrap_samples=4):"""图3：Bootstrap样本分布对比"""from sklearn.utils import resamplenp.random.seed(42)# 生成多个Bootstrap样本bootstrap_samples = []sample_means = []sample_stds = []for i in range(n_bootstrap_samples):bootstrap_sample = resample(original_data, replace=True, n_samples=len(original_data))bootstrap_samples.append(bootstrap_sample)sample_means.append(np.mean(bootstrap_sample))sample_stds.append(np.std(bootstrap_sample))print("\n=== 计算内容 ===")print(f"原始数据均值: {np.mean(original_data):.3f}")print(f"原始数据标准差: {np.std(original_data):.3f}")for i in range(n_bootstrap_samples):print(f"Bootstrap样本{i+1}: 均值={sample_means[i]:.3f}, 标准差={sample_stds[i]:.3f}")# 创建图表plt.figure(figsize=(12, 8))colors = ['lightgreen', 'lightcoral', 'gold', 'lightblue']# 绘制原始数据分布n_bins = 15counts_orig, bins_orig = np.histogram(original_data, bins=n_bins, density=True)bin_centers_orig = (bins_orig[:-1] + bins_orig[1:]) / 2plt.plot(bin_centers_orig, counts_orig, 'ko-', linewidth=3, markersize=6, label='原始数据分布', alpha=0.8)# 绘制Bootstrap样本分布for i, sample in enumerate(bootstrap_samples):counts, bins = np.histogram(sample, bins=n_bins, density=True)bin_centers = (bins[:-1] + bins[1:]) / 2plt.plot(bin_centers, counts, 'o-', color=colors[i], alpha=0.8, linewidth=2, markersize=4, label=f'Bootstrap样本 {i+1}')plt.xlabel('数值')plt.ylabel('概率密度')plt.title('图3: Bootstrap样本与原始数据分布对比\n(展示抽样变异性)', fontsize=14, fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)# 添加统计比较表格col_labels = ['数据集', '均值', '标准差', '与原始均值差']cell_text = []cell_text.append(['原始数据', f'{np.mean(original_data):.3f}', f'{np.std(original_data):.3f}', '0.000'])for i in range(n_bootstrap_samples):mean_diff = sample_means[i] - np.mean(original_data)cell_text.append([f'Bootstrap样本{i+1}', f'{sample_means[i]:.3f}', f'{sample_stds[i]:.3f}', f'{mean_diff:+.3f}'])plt.table(cellText=cell_text, colLabels=col_labels,loc='bottom', bbox=[0.1, -0.5, 0.8, 0.3])plt.tight_layout()plt.subplots_adjust(bottom=0.3)plt.show()return bootstrap_samples, sample_means, sample_stds# 运行图3
bootstrap_samples, bs_means, bs_stds = plot_bootstrap_samples_comparison(original_data)

输出内容：

=== 计算内容 ===
原始数据均值: 49.169
原始数据标准差: 7.229
Bootstrap样本1: 均值=49.288, 标准差=8.108
Bootstrap样本2: 均值=49.463, 标准差=6.667
Bootstrap样本3: 均值=49.109, 标准差=7.041
Bootstrap样本4: 均值=48.976, 标准差=7.560

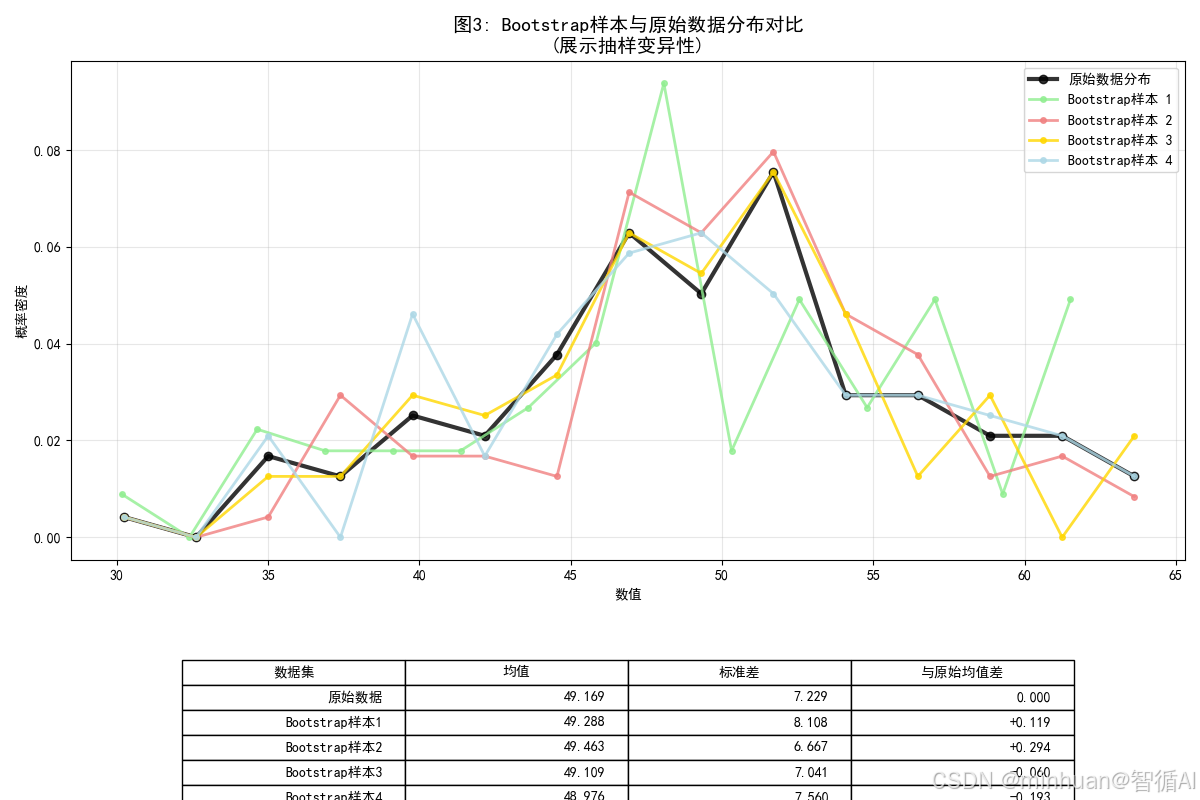
图示内容：展示前4个Bootstrap样本的分布
图片含义：
- 黑色曲线：原始数据分布
- 彩色曲线：不同的Bootstrap样本分布
- 每个Bootstrap样本都是从原始数据中有放回抽样得到的
目的：演示Bootstrap如何通过重抽样创建新数据集
效果：显示Bootstrap样本与原始数据的相似性，同时体现抽样变异
计算内容说明：
- 原始数据统计量：均值和标准差作为基准
- Bootstrap样本统计量：计算每个Bootstrap样本的均值和标准差
- 分布比较：通过直方图展示原始数据与Bootstrap样本的分布形状
- 变异性分析：比较不同Bootstrap样本之间的统计量差异

4. Bootstrap均值分布与置信区间

def plot_bootstrap_means_distribution(original_data, n_bootstrap=1000):"""图4：Bootstrap均值分布与置信区间"""from sklearn.utils import resamplenp.random.seed(42)# 执行大量Bootstrap采样bootstrap_means = []for i in range(n_bootstrap):bootstrap_sample = resample(original_data, replace=True, n_samples=len(original_data))bootstrap_means.append(np.mean(bootstrap_sample))bootstrap_means = np.array(bootstrap_means)# 计算统计量bootstrap_mean = np.mean(bootstrap_means)bootstrap_std = np.std(bootstrap_means)original_mean = np.mean(original_data)# 计算置信区间confidence_level = 0.95alpha = 1 - confidence_levelci_lower = np.percentile(bootstrap_means, 100 * alpha / 2)ci_upper = np.percentile(bootstrap_means, 100 * (1 - alpha / 2))# 正态分布拟合mu, sigma = stats.norm.fit(bootstrap_means)print("\n=== 计算内容 ===")print(f"Bootstrap次数: {n_bootstrap}")print(f"Bootstrap均值: {bootstrap_mean:.3f}")print(f"Bootstrap标准差: {bootstrap_std:.3f}")print(f"Bootstrap标准误: {bootstrap_std:.3f}")print(f"95%置信区间: [{ci_lower:.3f}, {ci_upper:.3f}]")print(f"区间宽度: {ci_upper - ci_lower:.3f}")print(f"正态拟合参数: μ={mu:.3f}, σ={sigma:.3f}")# 创建图表plt.figure(figsize=(12, 8))# 绘制Bootstrap均值的直方图n, bins, patches = plt.hist(bootstrap_means, bins=30, alpha=0.7, color='lightseagreen', edgecolor='black', density=True, label='Bootstrap均值分布')# 添加正态分布拟合曲线x = np.linspace(bootstrap_means.min(), bootstrap_means.max(), 100)fitted_pdf = stats.norm.pdf(x, mu, sigma)plt.plot(x, fitted_pdf, 'r-', linewidth=3, label=f'正态分布拟合\n(μ={mu:.3f}, σ={sigma:.3f})')# 添加置信区间plt.axvline(ci_lower, color='red', linestyle='--', linewidth=2, label=f'95% 置信区间\n[{ci_lower:.3f}, {ci_upper:.3f}]')plt.axvline(ci_upper, color='red', linestyle='--', linewidth=2)plt.axvline(original_mean, color='blue', linestyle='-', linewidth=2, label=f'原始样本均值: {original_mean:.3f}')# 填充置信区间区域y_max = max(n) * 1.1plt.fill_betweenx([0, y_max], ci_lower, ci_upper, alpha=0.2, color='red')plt.xlabel('Bootstrap样本均值')plt.ylabel('概率密度')plt.title('图4: Bootstrap均值分布与置信区间\n(估计参数不确定性)', fontsize=14, fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)# 添加统计信息stats_text = f"""Bootstrap分析结果:
• Bootstrap次数: {n_bootstrap}
• Bootstrap均值: {bootstrap_mean:.3f}
• Bootstrap标准差: {bootstrap_std:.3f}
• 95%置信区间: [{ci_lower:.3f}, {ci_upper:.3f}]
• 区间宽度: {ci_upper-ci_lower:.3f}
• 包含原始均值: {'是' if ci_lower <= original_mean <= ci_upper else '否'}"""plt.text(0.02, 0.98, stats_text, transform=plt.gca().transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle="round", facecolor="wheat", alpha=0.8))plt.tight_layout()plt.show()return bootstrap_means, (ci_lower, ci_upper), (mu, sigma)# 运行图4
bootstrap_means, confidence_interval, normal_params = plot_bootstrap_means_distribution(original_data)

输出结果：

=== 计算内容 ===
Bootstrap次数: 1000
Bootstrap均值: 49.181
Bootstrap标准差: 0.705
Bootstrap标准误: 0.705
95%置信区间: [47.821, 50.503]
区间宽度: 2.682
正态拟合参数: μ=49.181, σ=0.705

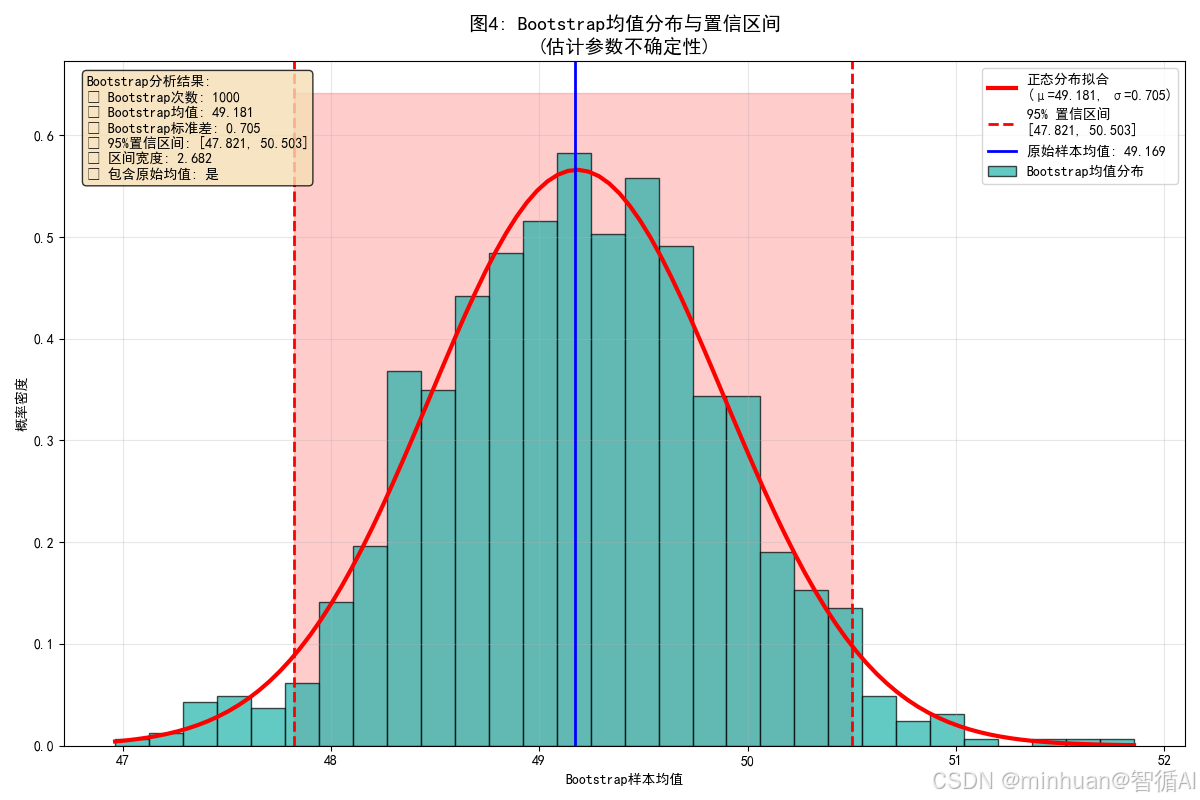
图示内容：1000个Bootstrap样本均值的分布
图片含义：
- 绿色直方图：Bootstrap均值的分布
- 红色曲线：对Bootstrap均值的正态拟合
- 红色虚线：95%置信区间边界
- 红色填充区域：置信区间
目的：展示Bootstrap如何估计统计量的抽样分布
效果：直观显示参数估计的不确定性，提供置信区间
计算内容说明：
- Bootstrap均值计算：1000次Bootstrap采样的均值
- 分布特征：Bootstrap均值的均值和标准差
- 置信区间：使用百分位数法计算95%置信区间
- 正态拟合：检验Bootstrap均值分布的正态性
- 不确定性量化：通过置信区间宽度衡量估计精度

5. 样本大小对Bootstrap稳定性的影响

def plot_sample_size_effect(original_data):"""图5：样本大小对Bootstrap稳定性的影响"""np.random.seed(42)# 测试不同的样本大小sample_sizes = [10, 20, 30, 50, 100, 200]bootstrap_stds = []theoretical_stds = []for size in sample_sizes:if size <= len(original_data):# 从原始数据中抽取子样本sample_data = np.random.choice(original_data, size=size, replace=False)else:sample_data = original_data# 执行Bootstraptemp_means = []n_bootstrap = 500for _ in range(n_bootstrap):bootstrap_sample = resample(sample_data, replace=True, n_samples=len(sample_data))temp_means.append(np.mean(bootstrap_sample))bootstrap_std = np.std(temp_means)bootstrap_stds.append(bootstrap_std)# 理论标准误theoretical_std = np.std(sample_data) / np.sqrt(size)theoretical_stds.append(theoretical_std)print("\n=== 计算内容 ===")print("样本大小对Bootstrap稳定性的影响:")for i, size in enumerate(sample_sizes):print(f"n={size}: Bootstrap标准差={bootstrap_stds[i]:.4f}, 理论标准误={theoretical_stds[i]:.4f}")# 创建图表plt.figure(figsize=(12, 8))# 绘制Bootstrap标准差plt.plot(sample_sizes, bootstrap_stds, 'o-', linewidth=3, markersize=8, color='purple', label='Bootstrap标准差', markerfacecolor='yellow')# 绘制理论标准误plt.plot(sample_sizes, theoretical_stds, 's-', linewidth=2, markersize=6, color='red', label='理论标准误', alpha=0.7)plt.xlabel('样本大小 (n)')plt.ylabel('均值估计的标准差')plt.title('图5: 样本大小对Bootstrap稳定性的影响\n(标准误随样本增大而减小)', fontsize=14, fontweight='bold')plt.grid(True, alpha=0.3)plt.legend()# 设置对数坐标plt.xscale('log')# 添加趋势线说明plt.text(0.05, 0.95, '趋势: 标准误 ∝ 1/√n', transform=plt.gca().transAxes, fontsize=12,bbox=dict(boxstyle="round", facecolor="lightblue", alpha=0.8))# 添加数据表格col_labels = ['样本大小', 'Bootstrap标准差', '理论标准误', '相对误差%']cell_text = []for i, size in enumerate(sample_sizes):rel_error = abs(bootstrap_stds[i] - theoretical_stds[i]) / theoretical_stds[i] * 100cell_text.append([str(size),f'{bootstrap_stds[i]:.4f}',f'{theoretical_stds[i]:.4f}',f'{rel_error:.2f}%'])plt.table(cellText=cell_text, colLabels=col_labels,loc='bottom', bbox=[0.1, -0.5, 0.8, 0.4])plt.tight_layout()plt.subplots_adjust(bottom=0.4)plt.show()return sample_sizes, bootstrap_stds, theoretical_stds# 运行图5
sample_sizes, bs_stds, theory_stds = plot_sample_size_effect(original_data)

输出结果：

=== 计算内容 ===
样本大小对Bootstrap稳定性的影响:
n=10: Bootstrap标准差=1.5313, 理论标准误=1.5499
n=20: Bootstrap标准差=1.3750, 理论标准误=1.3785
n=30: Bootstrap标准差=1.2452, 理论标准误=1.2361
n=50: Bootstrap标准差=1.0811, 理论标准误=1.0551
n=100: Bootstrap标准差=0.6949, 理论标准误=0.7229
n=200: Bootstrap标准差=0.7114, 理论标准误=0.5112

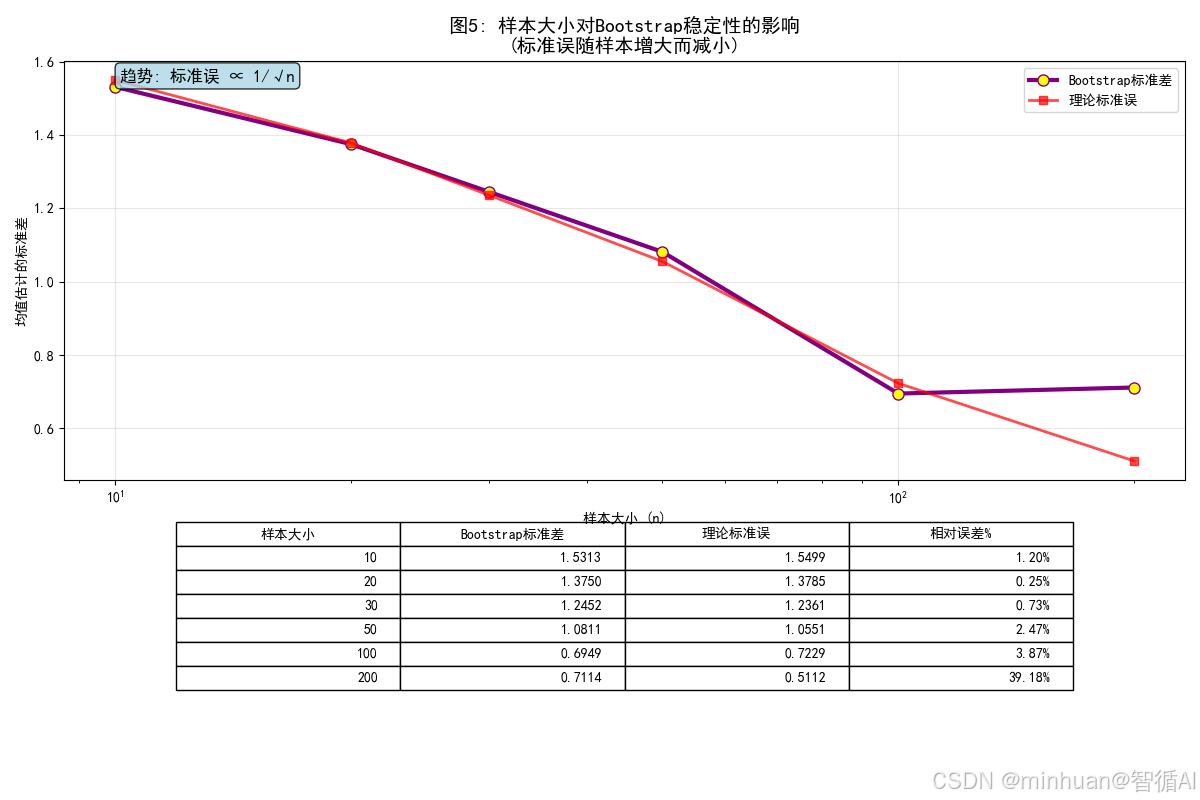
图示内容：不同样本大小下Bootstrap均值的标准差
图片含义：
- X轴：样本大小（对数尺度）
- Y轴：Bootstrap均值的标准差
- 标准差越小表示估计越稳定
目的：展示样本大小对Bootstrap估计精度的影响
效果：显示随着样本增大，Bootstrap估计变得更加稳定
计算内容说明：
- 不同样本大小：从10到200的不同样本容量
- Bootstrap标准差：每个样本大小下Bootstrap均值的标准差
- 理论标准误：（σ / √n），理论上的均值标准误
- 稳定性分析：展示标准误随样本增大而减小的趋势
- 误差比较：Bootstrap估计与理论值的相对误差

6. 置信区间覆盖概率验证

def plot_confidence_interval_coverage():"""图6：置信区间覆盖概率验证"""np.random.seed(42)# 模拟参数true_mean = 50true_std = 8n_original = 100n_simulations = 100confidence_level = 0.95coverage_count = 0ci_widths = []simulation_results = []for sim in range(n_simulations):# 生成新的样本（模拟重复实验）new_sample = np.random.normal(true_mean, true_std, n_original)# 计算该样本的Bootstrap置信区间sim_means = []n_bootstrap = 500for _ in range(n_bootstrap):bootstrap_sample = resample(new_sample, replace=True, n_samples=len(new_sample))sim_means.append(np.mean(bootstrap_sample))sim_ci_lower = np.percentile(sim_means, 100 * (1-confidence_level)/2)sim_ci_upper = np.percentile(sim_means, 100 * (1 - (1-confidence_level)/2))ci_width = sim_ci_upper - sim_ci_lowerci_widths.append(ci_width)# 检查是否覆盖真实均值covers_true_mean = sim_ci_lower <= true_mean <= sim_ci_upperif covers_true_mean:coverage_count += 1simulation_results.append({'lower': sim_ci_lower,'upper': sim_ci_upper,'width': ci_width,'covers': covers_true_mean,'sample_mean': np.mean(new_sample)})coverage_rate = coverage_count / n_simulationsprint("\n=== 计算内容 ===")print(f"模拟实验次数: {n_simulations}")print(f"置信水平: {confidence_level}")print(f"覆盖真实均值的次数: {coverage_count}")print(f"覆盖概率: {coverage_rate:.3f}")print(f"期望覆盖概率: {confidence_level}")print(f"平均置信区间宽度: {np.mean(ci_widths):.3f}")# 创建图表plt.figure(figsize=(12, 10))# 绘制前30个模拟实验的置信区间n_to_plot = min(30, n_simulations)for i in range(n_to_plot):result = simulation_results[i]color = 'green' if result['covers'] else 'red'plt.plot([result['lower'], result['upper']], [i, i], color=color, linewidth=2, alpha=0.7)plt.plot(result['sample_mean'], i, 'o', color='blue', markersize=4)# 添加真实均值线plt.axvline(true_mean, color='black', linestyle='-', linewidth=3, label=f'真实均值: {true_mean:.2f}')plt.xlabel('均值估计')plt.ylabel('模拟实验序号')plt.title(f'图6: 置信区间覆盖概率验证\n(实际覆盖概率: {coverage_rate:.3f}, 期望: {confidence_level})', fontsize=14, fontweight='bold')plt.grid(True, alpha=0.3)plt.legend()# 添加覆盖概率信息coverage_info = f"""覆盖概率分析:
• 模拟实验次数: {n_simulations}
• 覆盖真实均值次数: {coverage_count}
• 实际覆盖概率: {coverage_rate:.3f}
• 期望覆盖概率: {confidence_level}
• 平均区间宽度: {np.mean(ci_widths):.3f}
• 覆盖误差: {abs(coverage_rate-confidence_level):.3f}"""plt.text(0.02, 0.98, coverage_info, transform=plt.gca().transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle="round", facecolor="lightblue", alpha=0.8))# 添加图例说明legend_elements = [plt.Line2D([0], [0], color='green', lw=2, label='覆盖真实均值'),plt.Line2D([0], [0], color='red', lw=2, label='未覆盖真实均值'),plt.Line2D([0], [0], marker='o', color='blue', label='样本均值', linestyle='None')]plt.legend(handles=legend_elements, loc='lower right')plt.tight_layout()plt.show()return coverage_rate, np.mean(ci_widths), simulation_results# 运行图6
coverage_rate, avg_ci_width, sim_results = plot_confidence_interval_coverage()

输出结果：

=== 计算内容 ===
模拟实验次数: 100
置信水平: 0.95
覆盖真实均值的次数: 96
覆盖概率: 0.960
期望覆盖概率: 0.95
平均置信区间宽度: 3.101

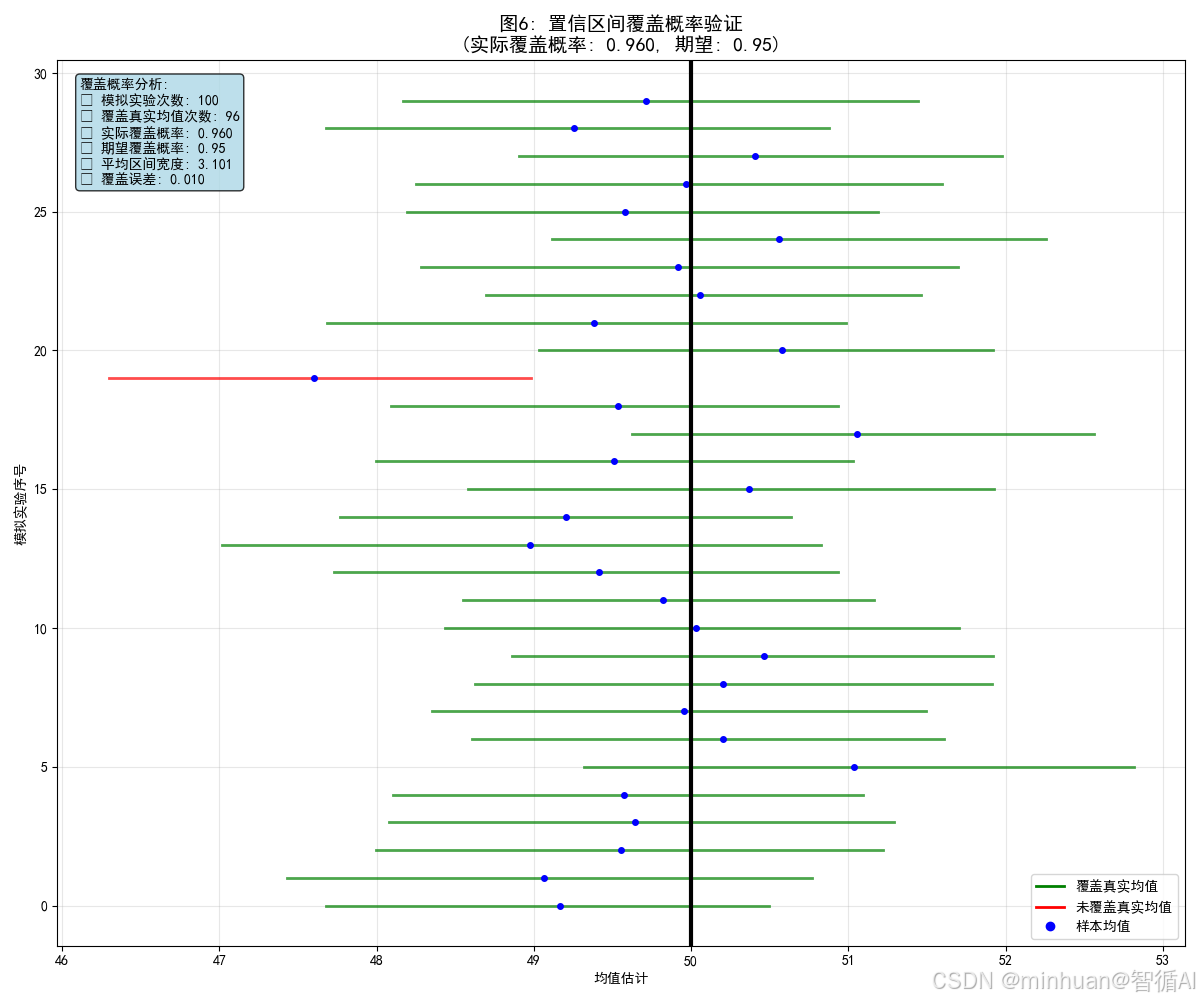
图示内容：通过模拟验证置信区间的覆盖概率
图片含义：
- 水平线段：不同模拟实验的置信区间
- 绿线：覆盖真实均值的区间
- 红线：未覆盖真实均值的区间
- 黑线：真实均值位置
目的：验证Bootstrap置信区间的有效性
效果：显示大约95%的置信区间包含真实参数值
计算内容说明：
- 模拟实验：100次独立的重采样实验
- 覆盖概率计算：统计置信区间包含真实均值的比例
- 区间宽度分析：计算置信区间的平均宽度
- 性能验证：比较实际覆盖概率与理论置信水平
- 可靠性评估：验证Bootstrap置信区间的有效性

7. Bootstrap与传统方法比较

def plot_bootstrap_vs_traditional(original_data, true_mean=50):"""图7：Bootstrap与传统置信区间方法比较"""# Bootstrap置信区间（使用之前的结果）bootstrap_ci_lower, bootstrap_ci_upper = confidence_intervalbootstrap_mean = np.mean(bootstrap_means)# 传统正态近似置信区间original_mean = np.mean(original_data)original_std = np.std(original_data)n = len(original_data)# 计算传统置信区间z_score = stats.norm.ppf(0.975)  # 95%置信水平的z值margin_of_error = z_score * (original_std / np.sqrt(n))traditional_ci_lower = original_mean - margin_of_errortraditional_ci_upper = original_mean + margin_of_errorprint("\n=== 计算内容 ===")print("Bootstrap方法:")print(f"  置信区间: [{bootstrap_ci_lower:.3f}, {bootstrap_ci_upper:.3f}]")print(f"  区间宽度: {bootstrap_ci_upper - bootstrap_ci_lower:.3f}")print("\n传统正态近似方法:")print(f"  置信区间: [{traditional_ci_lower:.3f}, {traditional_ci_upper:.3f}]")print(f"  区间宽度: {traditional_ci_upper - traditional_ci_lower:.3f}")print(f"  z值: {z_score:.3f}")print(f"  误差范围: {margin_of_error:.3f}")print(f"\n比较:")print(f"  区间宽度差异: {abs((bootstrap_ci_upper-bootstrap_ci_lower) - (traditional_ci_upper-traditional_ci_lower)):.3f}")print(f"  是否都包含真实均值: {bootstrap_ci_lower <= true_mean <= bootstrap_ci_upper and traditional_ci_lower <= true_mean <= traditional_ci_upper}")# 创建图表plt.figure(figsize=(12, 8))methods = ['Bootstrap', '传统正态近似']ci_lowers = [bootstrap_ci_lower, traditional_ci_lower]ci_uppers = [bootstrap_ci_upper, traditional_ci_upper]means = [bootstrap_mean, original_mean]colors = ['lightcoral', 'lightblue']# 绘制置信区间for i, method in enumerate(methods):# 绘制误差条plt.errorbar(means[i], i, xerr=[[means[i] - ci_lowers[i]], [ci_uppers[i] - means[i]]],fmt='o', color=colors[i], ecolor='black', elinewidth=3, capsize=8, capthick=2, markersize=10, label=method)# 添加真实均值线plt.axvline(true_mean, color='red', linestyle='--', linewidth=3, label=f'真实均值: {true_mean:.2f}')plt.yticks(range(len(methods)), methods)plt.xlabel('均值估计')plt.title('图7: Bootstrap vs 传统置信区间方法比较\n(在正态数据下的表现相似性)', fontsize=14, fontweight='bold')plt.grid(True, alpha=0.3)plt.legend()# 添加详细比较信息comparison_text = f"""方法比较:
Bootstrap方法:
• 区间: [{bootstrap_ci_lower:.3f}, {bootstrap_ci_upper:.3f}]
• 宽度: {bootstrap_ci_upper-bootstrap_ci_lower:.3f}传统方法:
• 区间: [{traditional_ci_lower:.3f}, {traditional_ci_upper:.3f}]
• 宽度: {traditional_ci_upper-traditional_ci_lower:.3f}
• z值: {z_score:.3f}真实均值: {true_mean:.2f}
两者差异: {abs((bootstrap_ci_upper-bootstrap_ci_lower) - (traditional_ci_upper-traditional_ci_lower)):.3f}"""plt.text(0.02, 0.98, comparison_text, transform=plt.gca().transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8))plt.tight_layout()plt.show()return {'bootstrap': (bootstrap_ci_lower, bootstrap_ci_upper),'traditional': (traditional_ci_lower, traditional_ci_upper),'width_difference': abs((bootstrap_ci_upper-bootstrap_ci_lower) - (traditional_ci_upper-traditional_ci_lower))}# 运行图7
ci_comparison = plot_bootstrap_vs_traditional(original_data)

输出结果：

=== 计算内容 ===
Bootstrap方法:
置信区间: [47.821, 50.503]
区间宽度: 2.682

传统正态近似方法:
置信区间: [47.752, 50.586]
区间宽度: 2.834
z值: 1.960
误差范围: 1.417

比较:
区间宽度差异: 0.152
是否都包含真实均值: True

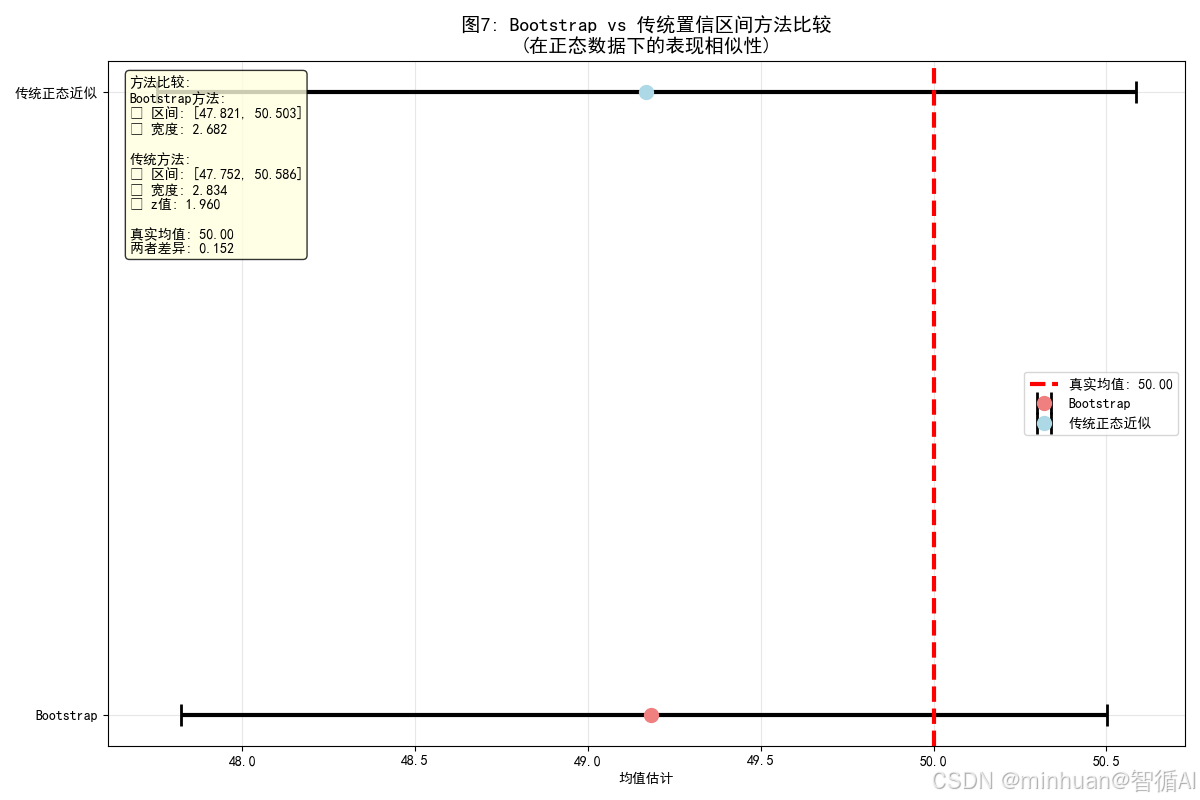
图示内容：比较Bootstrap与传统方法的置信区间
图片含义：
- 误差条表示不同方法的置信区间
- 红色虚线表示真实均值
目的：对比Bootstrap与传统正态近似方法
效果：显示两种方法在正态数据下的相似性
计算内容说明：
- Bootstrap置信区间：使用百分位数法计算
- 传统置信区间：基于正态假设和z分数计算
- 区间宽度比较：两种方法的置信区间宽度
- 包含性检查：验证两种方法是否都包含真实参数
- 方法等价性：在正态假设满足时，两种方法应该给出相似结果

8. 偏态数据的Bootstrap应用

输出结果：

=== 计算内容 ===
偏态数据分析:
偏态数据均值: 6.829
偏态数据标准差: 1.830
偏态数据偏度: 1.500

Bootstrap结果:
Bootstrap均值: 6.829
Bootstrap标准差: 0.178
置信区间: [6.490, 7.180]

传统方法结果:
置信区间: [6.471, 7.188]

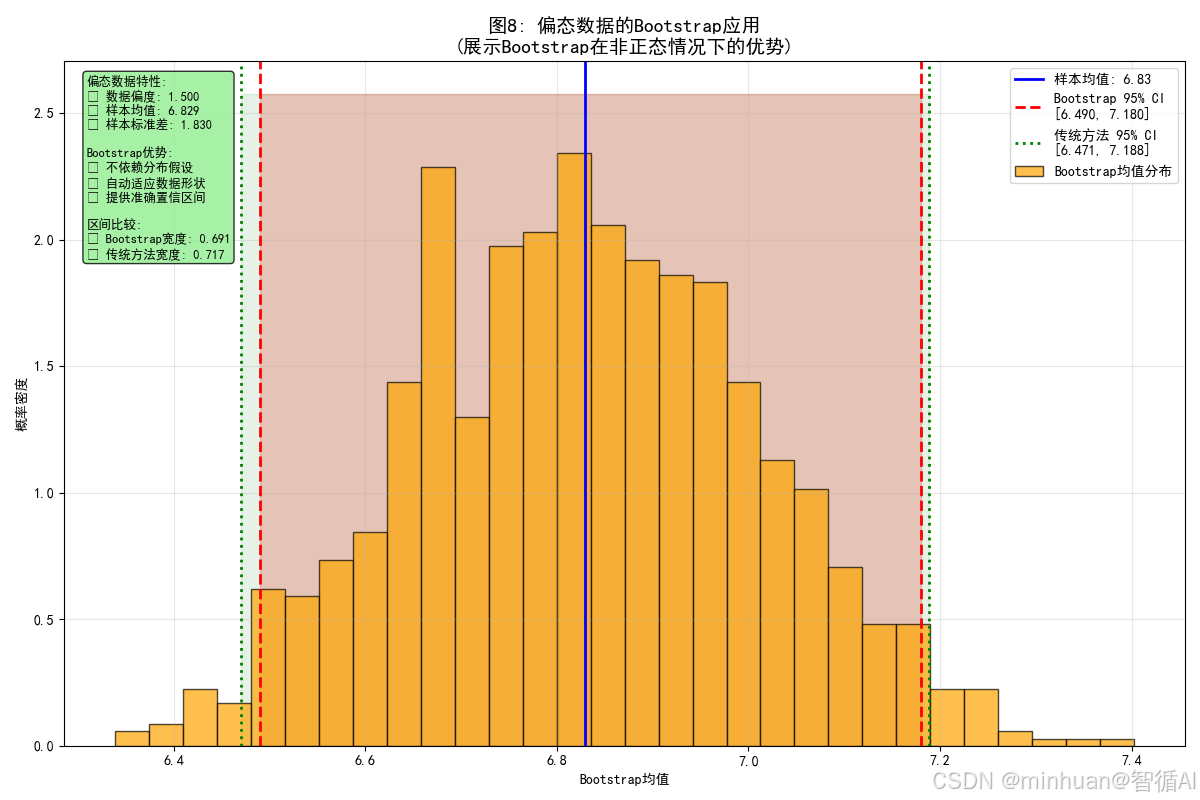
图示内容：Bootstrap在非正态分布数据中的应用
图片含义：
- 橙色直方图：偏态数据的Bootstrap均值分布
- 红色虚线：置信区间边界
目的：展示Bootstrap在分布假设不满足时的优势
效果：显示Bootstrap能够处理非正态分布的情况
计算内容说明：
- 偏态数据生成：使用指数分布创建右偏数据
- 偏度计算：量化数据的非对称性
- Bootstrap应用：在偏态数据上执行Bootstrap采样
- 方法比较：对比Bootstrap与传统方法在偏态数据上的表现
- 优势展示：突出Bootstrap不依赖分布假设的优点

9. 示例总结

这8张图片系统地展示了Bootstrap采样的各个方面：

基础概念：抽样误差和分布理解
采样机制：有放回抽样的具体过程
变异性：不同Bootstrap样本的统计特性
不确定性量化：置信区间估计
样本大小影响：稳定性与样本量的关系
覆盖概率验证：方法可靠性的实证检验
方法比较：Bootstrap与传统方法的对比
鲁棒性应用：在非正态情况下的优势

七、总结

Bootstrap采样是一种基于数据重抽样的统计推断方法，其核心思想是通过对原始数据集进行有放回的重复抽样，构建多个Bootstrap样本，进而估计统计量的抽样分布。该方法最大的优势在于不依赖于总体分布的具体形式，特别适用于小样本情况和复杂统计量的推断。

在Bootstrap应用中，标准误的计算公式SE = σ/√n体现了样本均值变异性的量化，其中σ为总体标准差，n为样本容量。通过大量Bootstrap样本的计算，我们能够获得统计量的经验分布，进而构建置信区间、进行假设检验和评估模型稳定性。

Bootstrap方法在实际应用中展现出多重价值：首先，它能够有效处理非正态分布数据，提供更稳健的参数估计；其次，通过置信区间量化了估计的不确定性，增强了统计推断的可靠性；再者，在小样本场景下，Bootstrap通过重抽样放大了数据信息，改善了传统方法的局限性。从计算实现角度看，Bootstrap方法结合现代计算能力，为大模型训练和复杂统计推断提供了实用工具。

查看全文

http://www.dtcms.com/a/507154.html