【计算机算法与分析】基于比较的排序算法
文章目录
- 一、开头:排序算法的核心价值与应用场景
- 二、核心内容:四种排序算法的深度解析
- 1、 插入排序:简单高效的基础排序方案
- 2. 堆排序:基于堆结构的高效排序
- 2.1. 堆结构
- 堆排序方法:
- 堆修复算法
- 特点分析
- 3、 归并排序:分治思想的经典实现
- 4、 快速排序:实际应用中的最优选择
- 三、理论分析:排序算法的共性与特性总结
- 1、 基础分析框架
- 2、 算法性能对比
- 3、 进阶应用:堆与优先队列
一、开头:排序算法的核心价值与应用场景
如果把杂乱的书籍按序号整理到书架,就如同排序算法将无序数据重排为递增序列——排序是众多复杂算法的基础组件,而基于比较数字大小实现的排序算法,更是日常开发与算法研究中的核心工具。
基于比较的排序算法各有优劣:
- 插入排序适合小规模数据,
- 堆排序兼顾稳定性与空间效率,
- 归并排序保障稳定高性能,
- 快速排序是实际应用的首选。
选择排序算法时,需根据数据规模、有序性、稳定性需求和空间限制综合判断。掌握这些算法的核心思想与特性,不仅能提升实际开发中的问题解决能力,更能为深入学习复杂算法奠定坚实基础。
二、核心内容:四种排序算法的深度解析
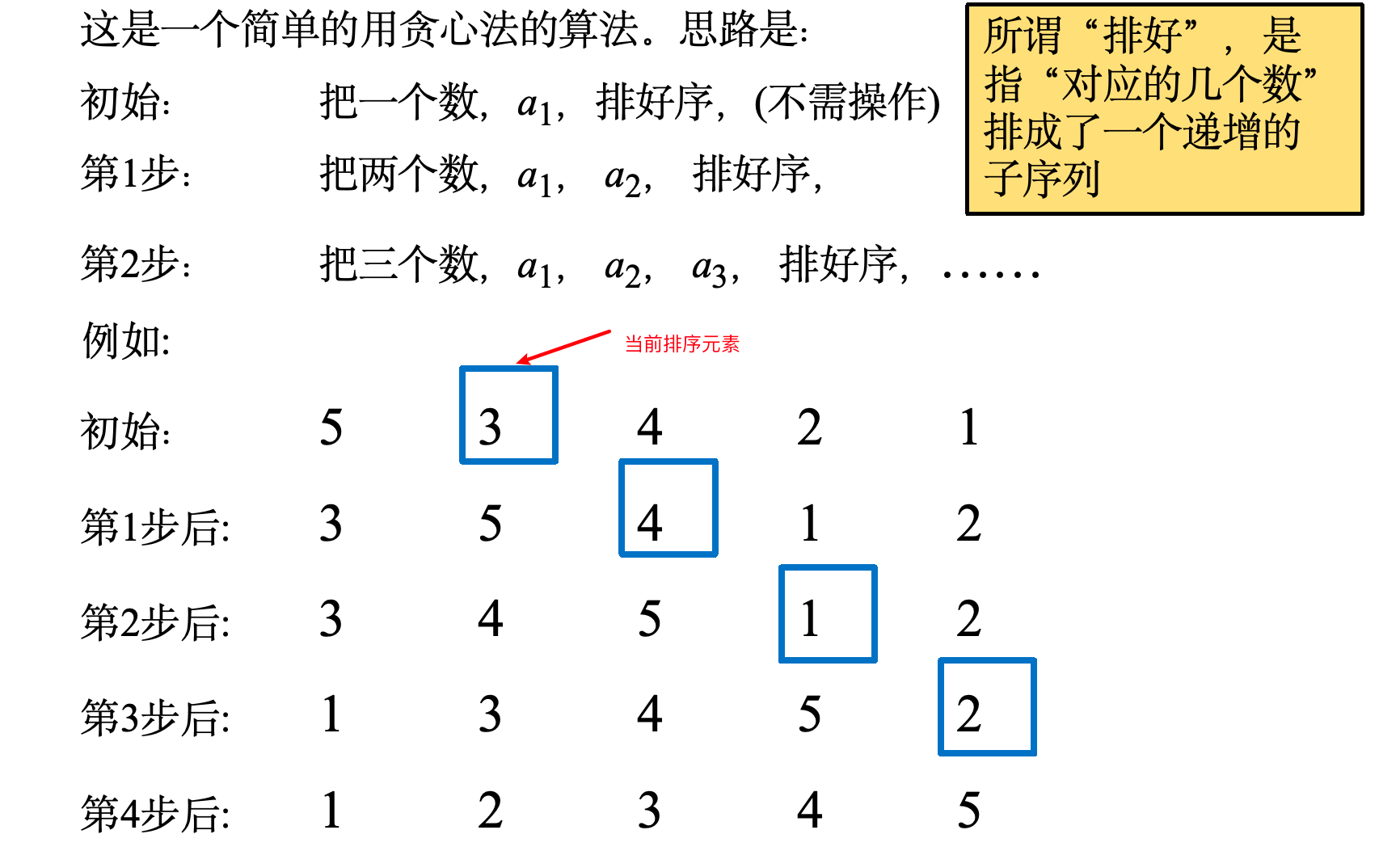
1、 插入排序:简单高效的基础排序方案
场景:适用于小规模数据排序、几乎有序的数据整理,或是作为复杂排序算法的子模块(如快速排序的优化),比如手牌整理、小型表单数据排序等。
方法:
- 步骤1:初始状态将第一个元素视为已排序子序列;
- 步骤2:依次将后续元素取出,与已排序子序列从后向前比较;
- 步骤3:找到合适位置插入该元素(其他元素一起移动),重复操作直至整个序列有序。
分析:
- 复杂度:最好情况为 Θ ( n ) \Theta(n) Θ(n)(数据已有序,遍历一遍判断即可),最坏和平均情况均为 Θ ( n 2 ) \Theta(n^2) Θ(n2);
- 特性:稳定排序、原地排序,无需额外存储空间,实现逻辑简单;
- 优势:对小规模数据或接近有序的数据效率较高,缺点是处理大规模数据时性能较差。
- 稳定排序:排序后,原序列中值相等的元素,相对位置不变(比如成绩相同的学生,仍保持原学号顺序)。
- 原地排序:排序时不用额外开辟和数据规模成正比的空间,只需要几个临时变量就行(不占太多额外内存)。
2. 堆排序:基于堆结构的高效排序
2.1. 堆结构
堆是一种特殊的完全二叉树数据结构,具有以下特点:
- 结构层面:
- 是有(n)个结点(含叶子结点)的完全二叉树,
- 所有叶结点出现在树的最底下二层;
- 倒数第二层的所有内结点出现在所有叶结点的左边;
- 除最后一个内结点可只有一个左儿子外,每个内结点必须有2个儿子。
- 二叉树高度为 h = ⌊ lg n ⌋ h = \lfloor\lg n\rfloor h=⌊lgn⌋。
- 是有(n)个结点(含叶子结点)的完全二叉树,
- 数值顺序层面:
- 若任何一个内结点中的数值大于或等于其所有儿子结点中的数值,称为最大堆;
- 若父结点中的数字小于或等于其所有儿子结点中的数字,称为最小堆。
本章讨论最大堆,用于实现从小到大的排序,且最大堆的根结点数值最大。
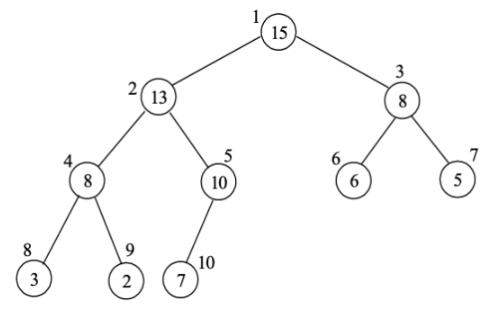
堆的结构:

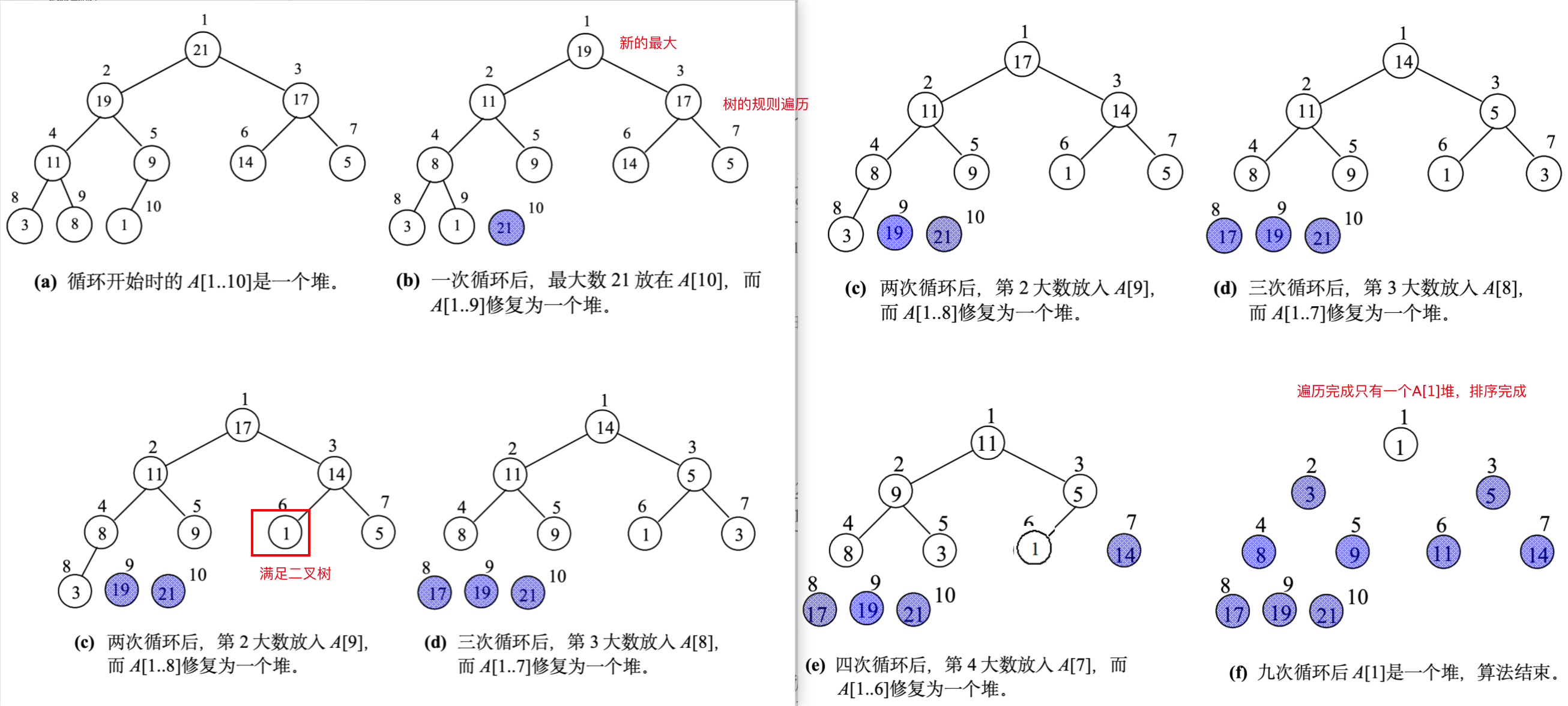
堆排序方法:
堆排序算法是利用堆这种数据结构进行排序的算法,主要分为建堆和排序两个关键步骤,用于实现数据的从小到大排序,以下是详细说明:
建堆阶段
堆排序开始前,需先将输入数据组织成一个最大堆(最大堆满足父节点值大于等于子节点值)。
- 方法:先把数字随意放到二叉树对应的数组中,再通过递归算法调整为堆。
- 递归算法(
Build-Max-Heap):
- 对于以
A[i]为根的子树,先确定其左儿子序号l = 2i和右儿子序号r = 2i + 1。- 若左儿子存在(
l ≤ n),递归对左子树调用Build-Max-Heap;若右儿子存在(r ≤ n),递归对右子树调用Build-Max-Heap。- 最后调用
Max-Heapify方法,确保以A[i]为根的子树满足最大堆的性质。- 当调用
Build-Max-Heap(A[1..n], 1)后,数组A[1..n]就变成了一个最大堆,建堆的时间复杂度为Θ(n)。
排序阶段
在数组
A[1..n]建堆完成后,执行堆排序:
- 初始化堆的大小
Heap - size = n。- 当堆的大小
heap - size > 1时,循环执行以下操作:
- 交换堆顶元素(数组第一个元素
A[1],即最大元素)和堆的最后一个元素A[heap - size],此时最大元素被放到了数组的末尾,成为已排序部分的元素。- 将堆的大小减1(
heap - size = heap - size - 1),意味着已排序部分的元素不再参与堆的调整。- 对新的堆顶元素(原堆的最后一个元素)调用
Max-Heapify方法,调整剩余的堆,使其重新成为最大堆,以便下一次取出最大元素。- 循环结束后,数组
A[1..n]就完成了从小到大的排序。
堆排序的整体时间复杂度为Θ(nlgn),它是一种原地排序算法(不需要额外的大规模存储空间),但不是稳定排序算法(相等元素的相对位置可能改变)。
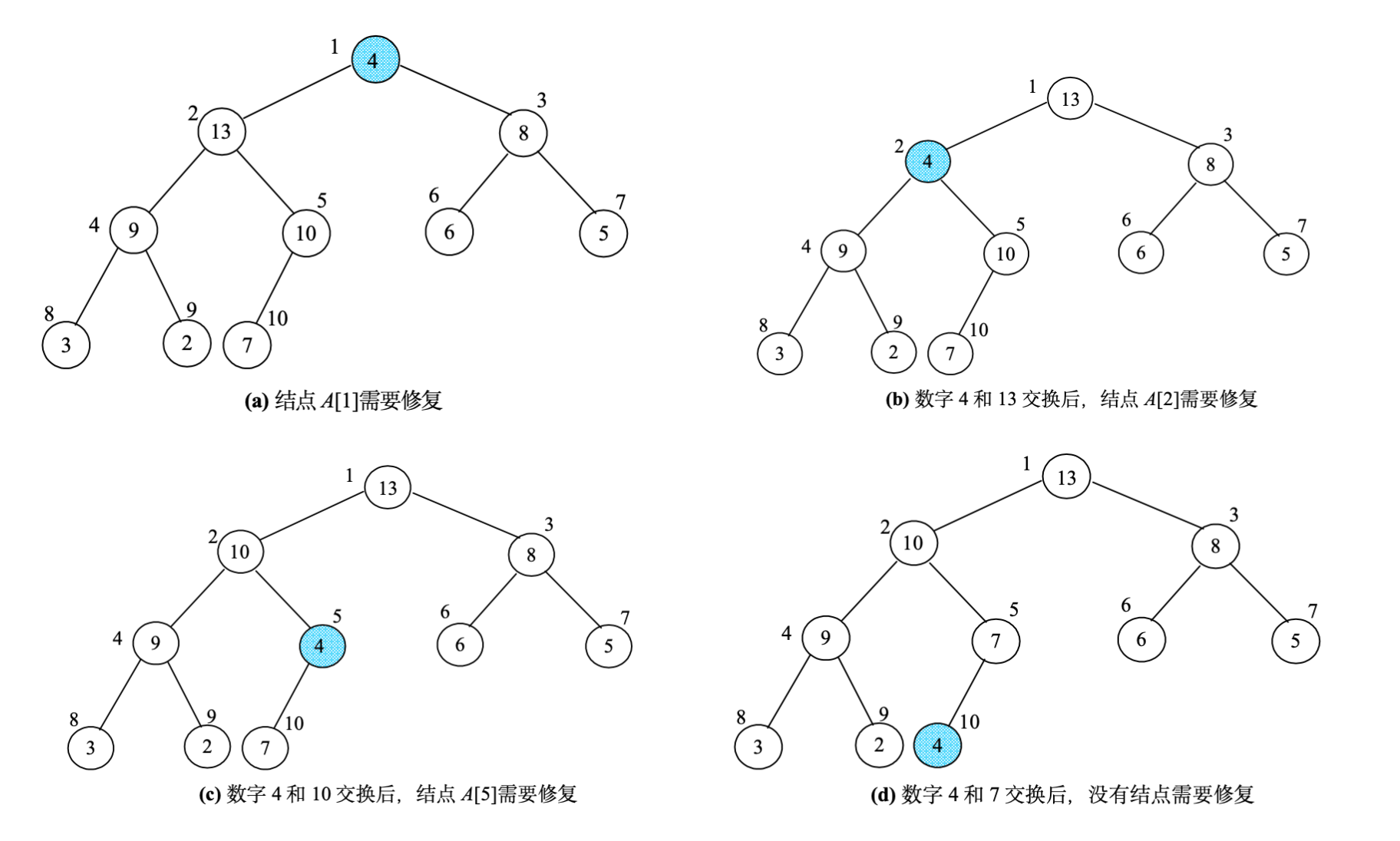
堆修复算法
特点分析
-
复杂度:建堆过程为 Θ ( n ) \Theta(n) Θ(n),堆修复为 O ( lg n ) O(\lg n) O(lgn),整体最坏、最好和平均情况均为 Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn);
-
特性:原地排序,非稳定排序;
-
优势:时间复杂度稳定,空间开销小;缺点是实际比较次数 (2n lg n \lg n lgn) 多于归并排序,对缓存不友好。
-
作为优先队列:堆还可以被许多算法用来进行数据的动态管理和修改,比如插入一个数据(Insert),刪除一个数据(delete),减少(或增加)一个数据的值(increase or decrease),找到最大(或最小)的数等。能够有效提供这些操作的数据结构都称为优先队列(Priority queue)。
3、 归并排序:分治思想的经典实现
场景:适用于大规模数据排序、需要稳定排序的场景,如外部排序(数据超出内存)、多字段排序后的结果保留等。
方法:
- 步骤1:将序列递归划分为两个等长(或近似等长)的子序列,直至子序列长度为1;
- 步骤2:设计合并算法,将两个有序子序列合并为一个有序序列(双指针遍历,依次选取较小元素);
- 步骤3:逐层合并子序列,最终得到完整的有序序列。
分析:
- 复杂度:最坏、最好和平均情况均为 Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn),且隐含系数为1,执行效率高;
- 特性:稳定排序,非原地排序,需额外 Ω ( n ) \Omega(n) Ω(n)的存储空间;
- 优势:时间复杂度稳定,适合处理大规模数据;缺点是空间开销较大,递归调用可能带来堆栈开销。
4、 快速排序:实际应用中的最优选择
场景:适用于大多数通用排序场景,如数据库查询优化、编程语言内置排序函数(如C++的sort),尤其适合内存中的大规模数据排序。
方法:
- 步骤1:选择序列中一个元素作为主元(如末尾元素);
- 步骤2:通过划分算法将序列分为两部分,左部元素均小于等于主元,右部元素均大于等于主元;
- 步骤3:递归对左右两部分执行快速排序,无需额外合并操作。
分析:
- 复杂度:平均情况为 Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn)(隐含系数1.39),最好情况为 Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn),最坏情况为 Θ ( n 2 ) \Theta(n^2) Θ(n2)(序列已有序或逆序);
- 特性:原地排序,非稳定排序;
- 优势:平均性能优异,空间开销小,对缓存友好;缺点是最坏情况性能较差,可通过随机选择主元优化。
三、理论分析:排序算法的共性与特性总结
1、 基础分析框架
基于比较的排序算法的核心性能指标包括时间复杂度(比较次数)、空间复杂度(额外存储)、稳定性(相同元素相对位置是否保留)和原地性(是否仅需常数额外空间)。其中,时间复杂度的下界为 Ω ( n lg n ) \Omega(n\lg n) Ω(nlgn),归并排序、堆排序和快速排序均达到了这一渐进最优性能。
2、 算法性能对比
| 算法 | 原地排序? | 时间复杂度 | 稳定排序? | 平均情况隐含系数 |
|---|---|---|---|---|
| 插入排序 | 是 | 最好: Θ ( n ) \Theta(n) Θ(n);最坏/平均: Θ ( n 2 ) \Theta(n^2) Θ(n2) | 是 | N/A |
| 归并排序 | 否 | 所有情况: Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn) | 是 | 1 |
| 堆排序 | 是 | 所有情况: Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn) | 否 | 2 |
| 快速排序 | 是 | 平均: Θ ( n lg n ) \Theta(n\lg n) Θ(nlgn);最坏: Θ ( n 2 ) \Theta(n^2) Θ(n2) | 否 | 1.39 |
3、 进阶应用:堆与优先队列
堆结构除用于排序外,还可高效实现优先队列,支持插入元素( O ( lg n ) O(\lg n) O(lgn))、提取最大值( O ( lg n ) O(\lg n) O(lgn))、修改元素值( O ( lg n ) O(\lg n) O(lgn))等操作,广泛应用于任务调度、最短路径算法(如Dijkstra算法)等场景。