「用Python来学微积分」4. 极坐标方程与参数方程
一、极坐标系
1. 平面直角坐标系的建立
在平面上,当取定两条互相垂直的直线的交点为原点,并确定了度量单位和两条直线的方向,就建立了平面直角坐标系。
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D# 支持中文
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
# 支持负数
plt.rcParams['axes.unicode_minus'] = Falsedef create_2d_cartesian_system(x_range=(-5, 5), y_range=(-5, 5), figsize=(8, 6)):"""创建二维直角坐标系"""fig, ax = plt.subplots(figsize=figsize)# 设置坐标轴范围ax.set_xlim(x_range[0], x_range[1])ax.set_ylim(y_range[0], y_range[1])# 设置坐标轴居中ax.spines['left'].set_position('zero')ax.spines['bottom'].set_position('zero')ax.spines['right'].set_color('none')ax.spines['top'].set_color('none')# 添加箭头ax.annotate('', xy=(x_range[1]-0.2, 0), xytext=(x_range[1]-0.8, 0),arrowprops=dict(arrowstyle="->", lw=1.2, color='black'))ax.annotate('', xy=(0, y_range[1]-0.2), xytext=(0, y_range[1]-0.8),arrowprops=dict(arrowstyle="->", lw=1.2, color='black'))# 设置标签ax.text(x_range[1]-0.5, -0.5, 'x', fontsize=14, fontweight='bold')ax.text(0.2, y_range[1]-0.5, 'y', fontsize=14, fontweight='bold')# 设置刻度x_ticks = np.arange(x_range[0], x_range[1]+1, 1)y_ticks = np.arange(y_range[0], y_range[1]+1, 1)ax.set_xticks(x_ticks[x_ticks != 0])ax.set_yticks(y_ticks[y_ticks != 0])# 标记原点ax.plot(0, 0, 'ko', markersize=4)ax.text(-0.3, -0.5, 'O', fontsize=12, fontweight='bold')# 添加网格ax.grid(True, linestyle='--', alpha=0.7)ax.set_title('二维直角坐标系', fontsize=16, pad=20)return fig, axif __name__ == "__main__":# 1. 二维直角坐标系fig1, ax1 = create_2d_cartesian_system()# 添加一个示例函数 y = xx = np.linspace(-4, 4, 100)y = xax1.plot(x, y, 'b-', linewidth=2, label='y = x')ax1.legend()plt.show()
运行结果:
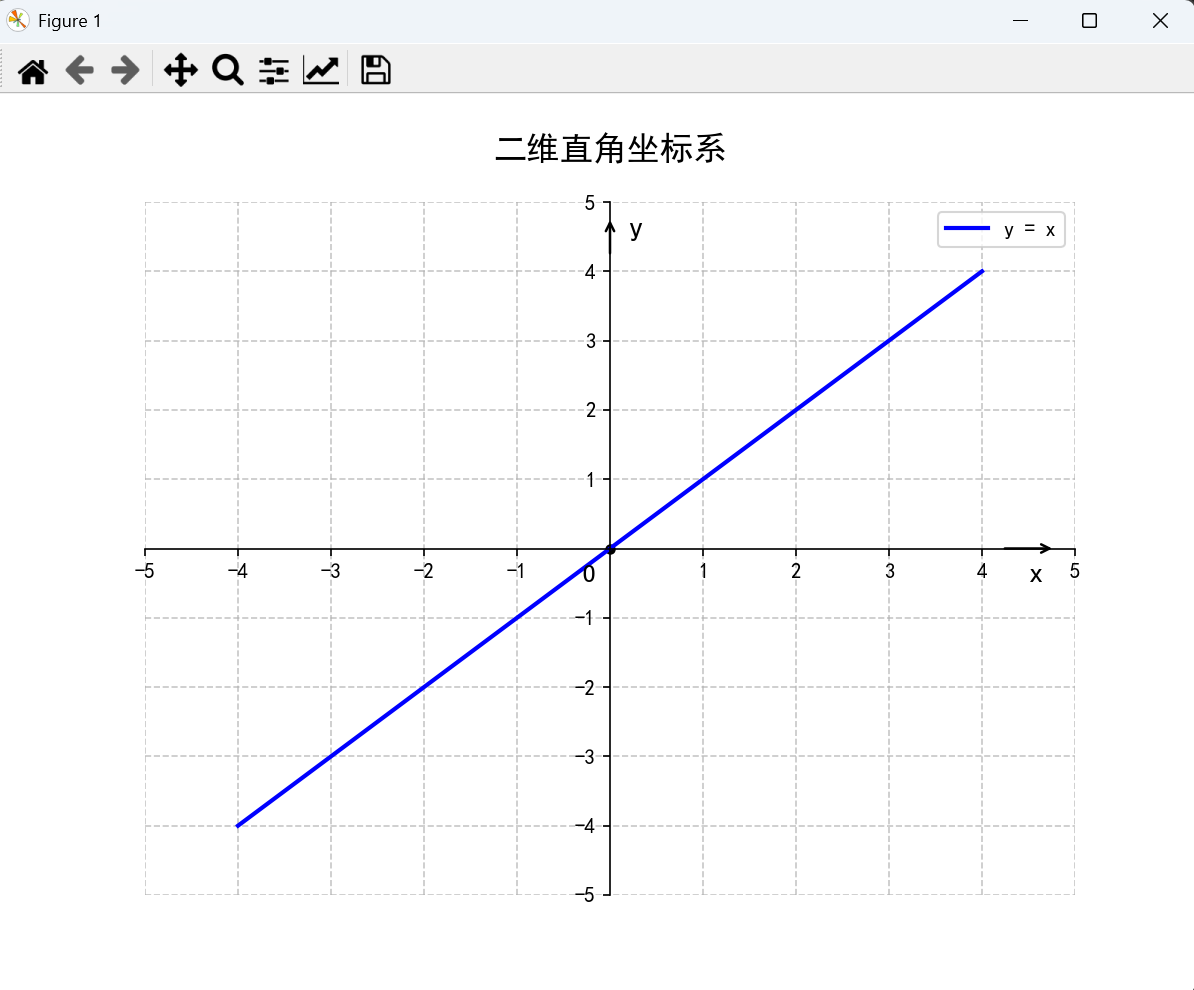
2. 空间直角坐标系的建立
在空间中,选择两两垂直且交于一点的三条直线,当取定这三条直线的交点为原点,并确定了度量单位和这三条直线的放下,就建立了空间指标坐标系。
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D# 支持中文
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
# 支持负数
plt.rcParams['axes.unicode_minus'] = Falsedef create_3d_cartesian_system(x_range=(-5, 5), y_range=(-5, 5), z_range=(-5, 5), figsize=(10, 8)):"""创建三维直角坐标系"""fig = plt.figure(figsize=figsize)ax = fig.add_subplot(111, projection='3d')# 设置坐标轴范围ax.set_xlim(x_range[0], x_range[1])ax.set_ylim(y_range[0], y_range[1])ax.set_zlim(z_range[0], z_range[1])# 设置标签ax.set_xlabel('X轴', fontsize=12)ax.set_ylabel('Y轴', fontsize=12)ax.set_zlabel('Z轴', fontsize=12)# 设置刻度ax.set_xticks(np.arange(x_range[0], x_range[1]+1, 2))ax.set_yticks(np.arange(y_range[0], y_range[1]+1, 2))ax.set_zticks(np.arange(z_range[0], z_range[1]+1, 2))# 标记原点ax.scatter(0, 0, 0, color='black', s=50)ax.text(0.2, 0.2, 0.2, 'O', fontsize=12, fontweight='bold')ax.set_title('三维直角坐标系', fontsize=16, pad=20)return fig, axif __name__ == "__main__": # 三维直角坐标系fig2, ax2 = create_3d_cartesian_system()# 添加一个示例点ax2.scatter(2, 3, 4, color='red', s=100, label='点(2, 3, 4)')ax2.legend()plt.show()
运行结果:
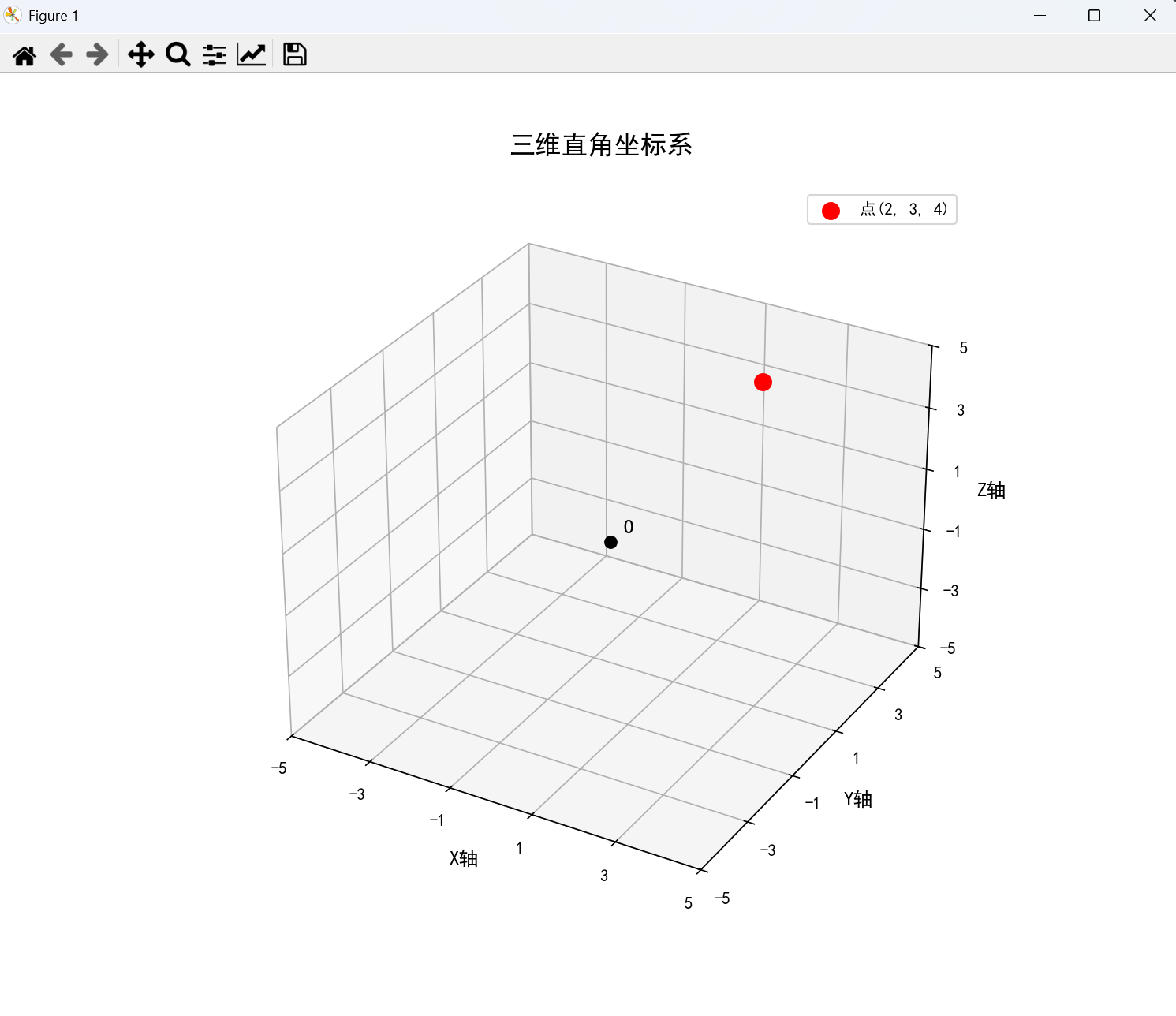
3. 极坐标系的建立
在平面上取一个定点O,自O引一条射线 Ox,同时确定单位长度和计算角度的正方向(通常取逆时针为正方向),这样就建立了极坐标系,其中O为极点,射线Ox为极轴。
设M是平面上的任意一点,p表示OM的长度,θ\thetaθ 表示射线Ox为始边,OM为终边的所成的角。那么有序对数(p,θ)(p,\theta)(p,θ) 称为点M的极坐标,其中 p 称为极径,θ\thetaθ 称为极角。
约定:极点的极坐标是p = 0, θ\thetaθ 可以取任意角。
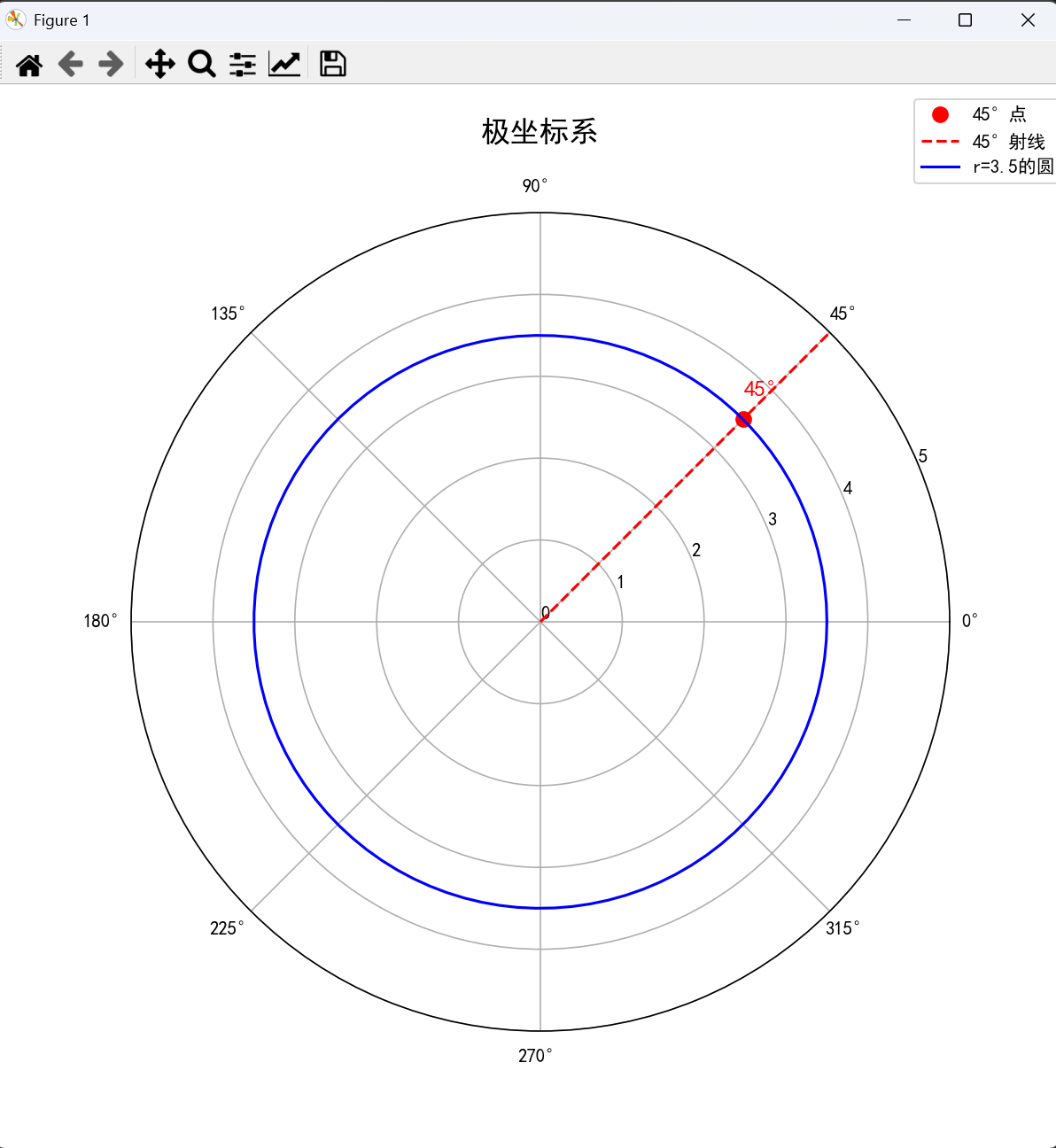
3. 直角坐标与极坐标的互化
以直角坐标系的O为极点,x轴正半轴为极轴,且在两坐标系中取相同的单位长度,平面内的任一点P的直角坐标、极坐标分别为(x,y) 和 (p,θ)(p,\theta)(p,θ) , 则
{x=pcosθ,y=psinθ, \begin{cases} x = pcos \theta, \\ y = psin \theta, \end{cases} {x=pcosθ,y=psinθ,
{p2=x2+y2,tanθ=yx(x≠0) \begin{cases} p^2 = x^2 + y^2, \\ \tan \theta = \frac{y}{x} (x \neq 0) \end{cases} {p2=x2+y2,tanθ=xy(x=0)
二、极坐标方程
1. 直线的极坐标方程
若直线 l 过点 M(P0,θ0)M(P_0,\theta_0)M(P0,θ0) , 且极轴到此直线的角为 α\alphaα , 则它的方程为
psin(θ−α)=p0sin(θ0−α) p \sin(\theta - \alpha) = p_0 \sin(\theta_0 - \alpha) psin(θ−α)=p0sin(θ0−α)
几个特殊位置的直线的极坐标方程:
(1) 经过极点 θ=α\theta = \alphaθ=α
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 1. 演示经过极点的直线:θ = α
print("1. 经过极点的直线方程:θ = π/4")
theta_constant = np.pi / 4
rho_values1 = np.linspace(0, 5, 100)
theta_values1 = np.full_like(rho_values1, theta_constant)
ax.plot(theta_values1, rho_values1, 'r-', linewidth=2, label='经过极点: θ = π/4')# 标记极点
ax.plot(0, 0, 'ro', markersize=8, label='极点')
# 添加图例和装饰
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
plt.tight_layout()
plt.show()
运行结果:
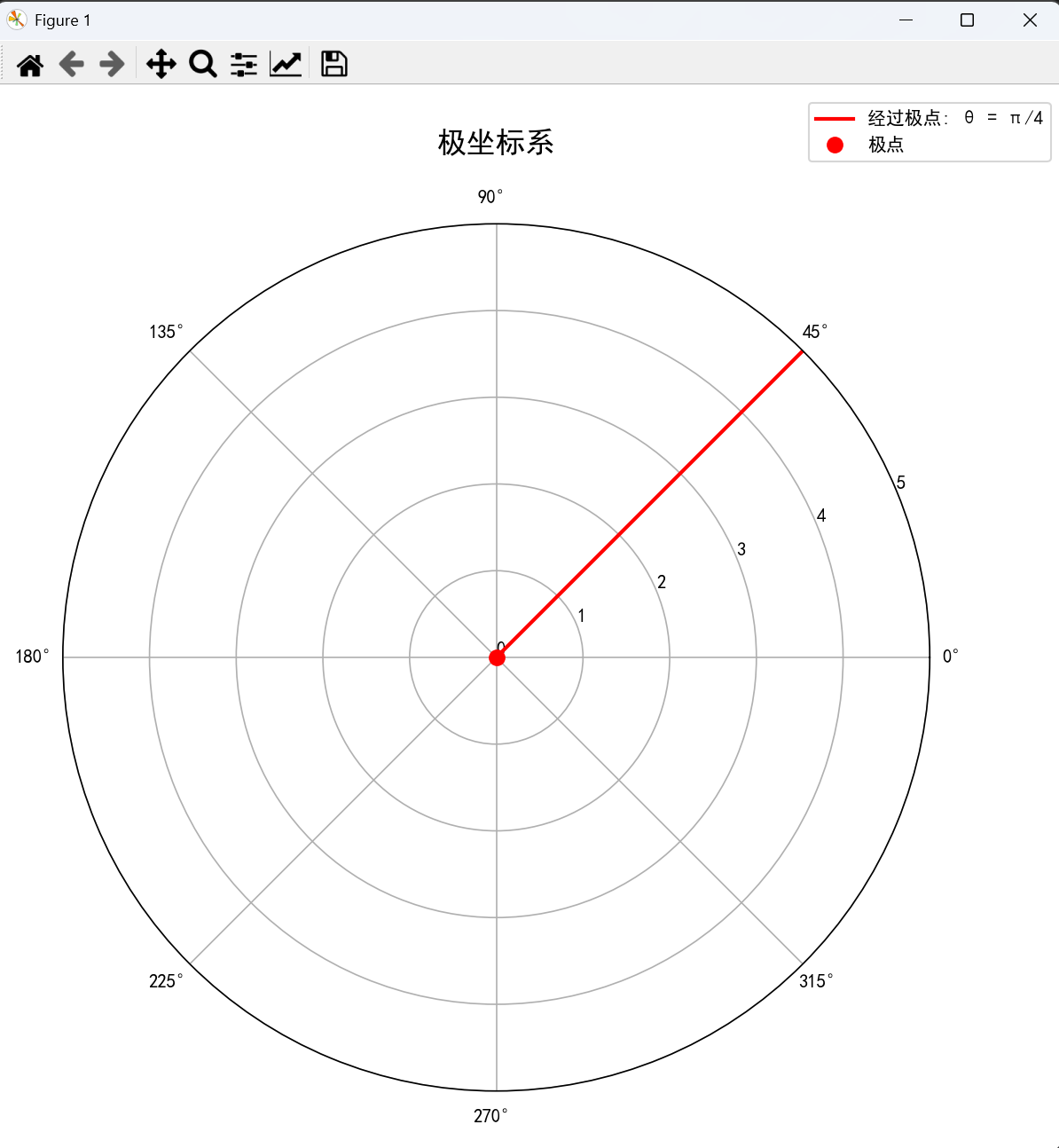
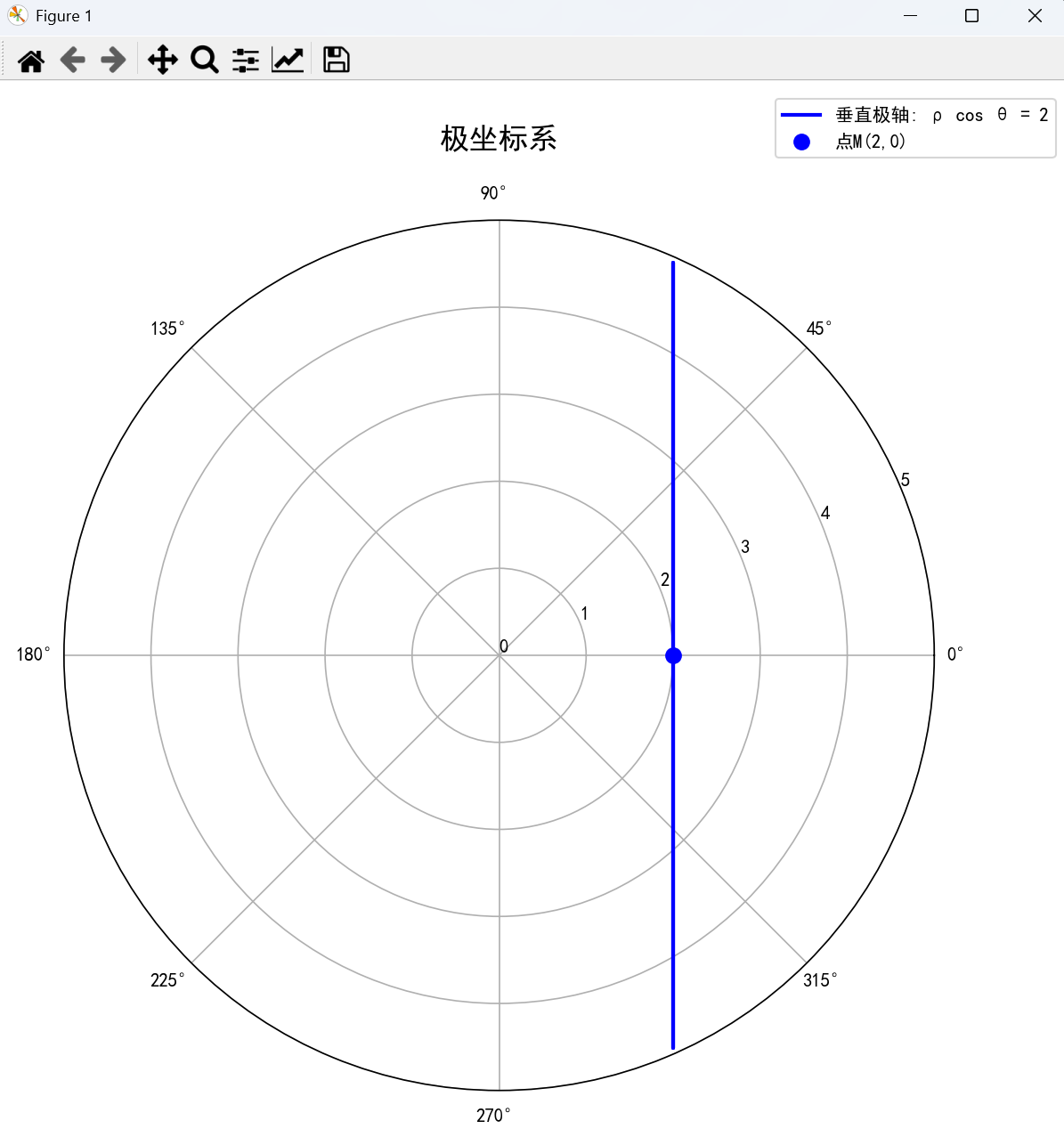
(2) 经过定点 M(a, 0), 且与极轴垂直
pcosθ=α p\cos \theta = \alpha pcosθ=α
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 生成θ值(避开cosθ=0的点)
theta1 = np.linspace(0.01, np.pi/2 - 0.01, 100) # 第一象限
theta2 = np.linspace(3*np.pi/2 + 0.01, 2*np.pi - 0.01, 100) # 第四象限
theta_values2 = np.concatenate([theta1, theta2])
# 点(a,0)
a = 2
# 计算ρ值:ρ = a / cosθ
rho_values2 = a / np.cos(theta_values2)
# 过滤掉ρ值过大的点(保持图形清晰)
mask = (rho_values2 <= 5) & (rho_values2 >= 0)
theta_values2 = theta_values2[mask]
rho_values2 = rho_values2[mask]
ax.plot(theta_values2, rho_values2, 'b-', linewidth=2, label='垂直极轴: ρ cos θ = 2')
# 标记点M(a,0) = (2,0)
ax.plot(0, a, 'bo', markersize=8, label='点M(2,0)')
# 添加图例和装饰
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
plt.tight_layout()
plt.show()
运行结果:
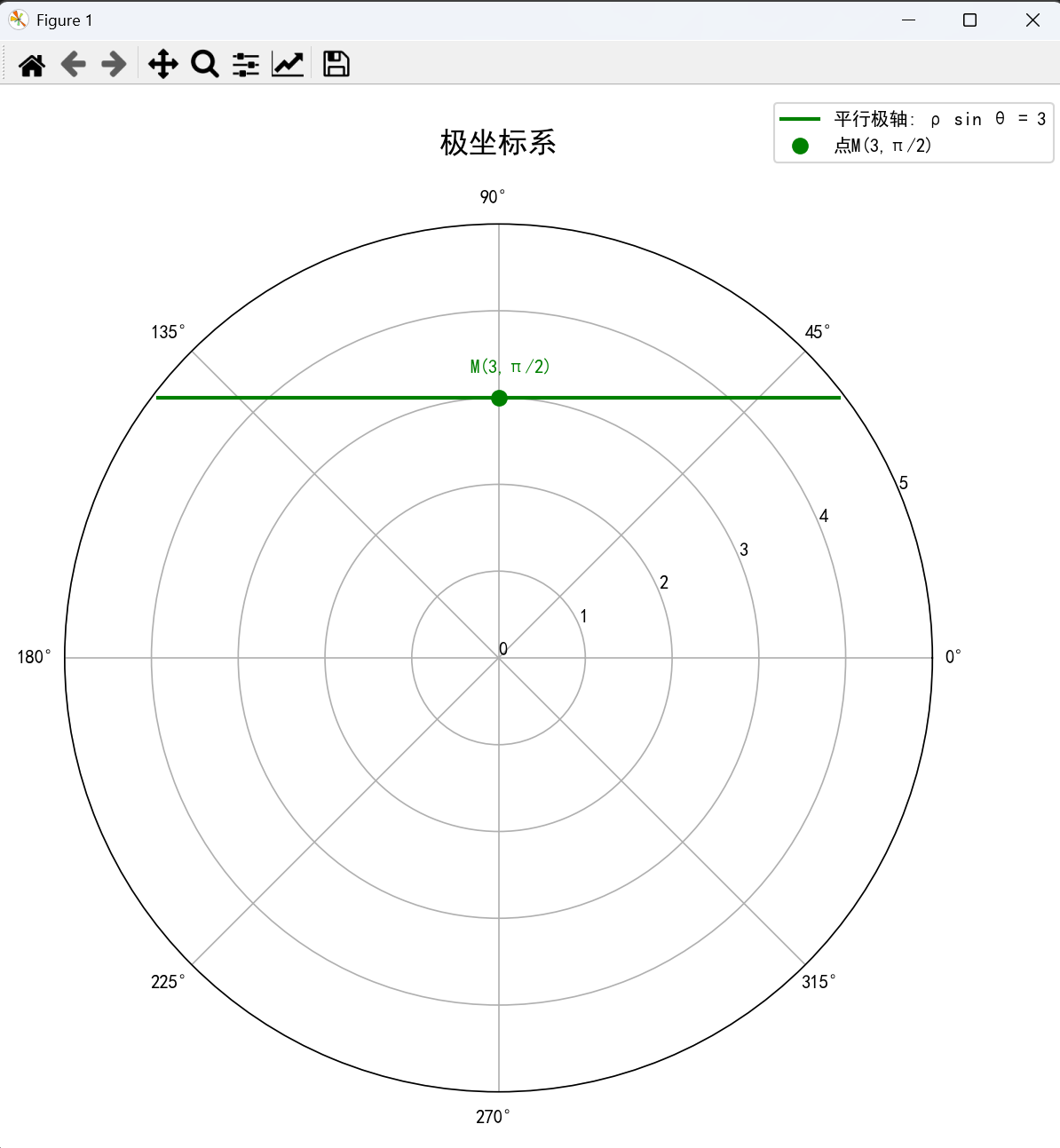
(3) 经过定点 M(b,π2)M(b, \frac{\pi}{2})M(b,2π) , 且与极轴平行
psinθ=b
p\sin \theta = b
psinθ=b
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 生成θ值(避开sinθ=0的点)
theta_values3 = np.linspace(0.01, np.pi - 0.01, 200)
# 经过点(b,π/2)的水平直线的参数
b = 3
# 计算ρ值:ρ = b / sinθ
rho_values3 = b / np.sin(theta_values3)
# 过滤掉ρ值过大的点
mask = (rho_values3 <= 5) & (rho_values3 >= 0)
theta_values3 = theta_values3[mask]
rho_values3 = rho_values3[mask]
ax.plot(theta_values3, rho_values3, 'g-', linewidth=2, label='平行极轴: ρ sin θ = 3')
# 标记点M(b,π/2) = (3,π/2)
ax.plot(np.pi/2, b, 'go', markersize=8, label='点M(3,π/2)')
# 添加图例和装饰
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
ax.text(np.pi/2 + 0.1, b + 0.3, 'M(3,π/2)', fontsize=10, color='green')
plt.tight_layout()
plt.show()
运行结果:
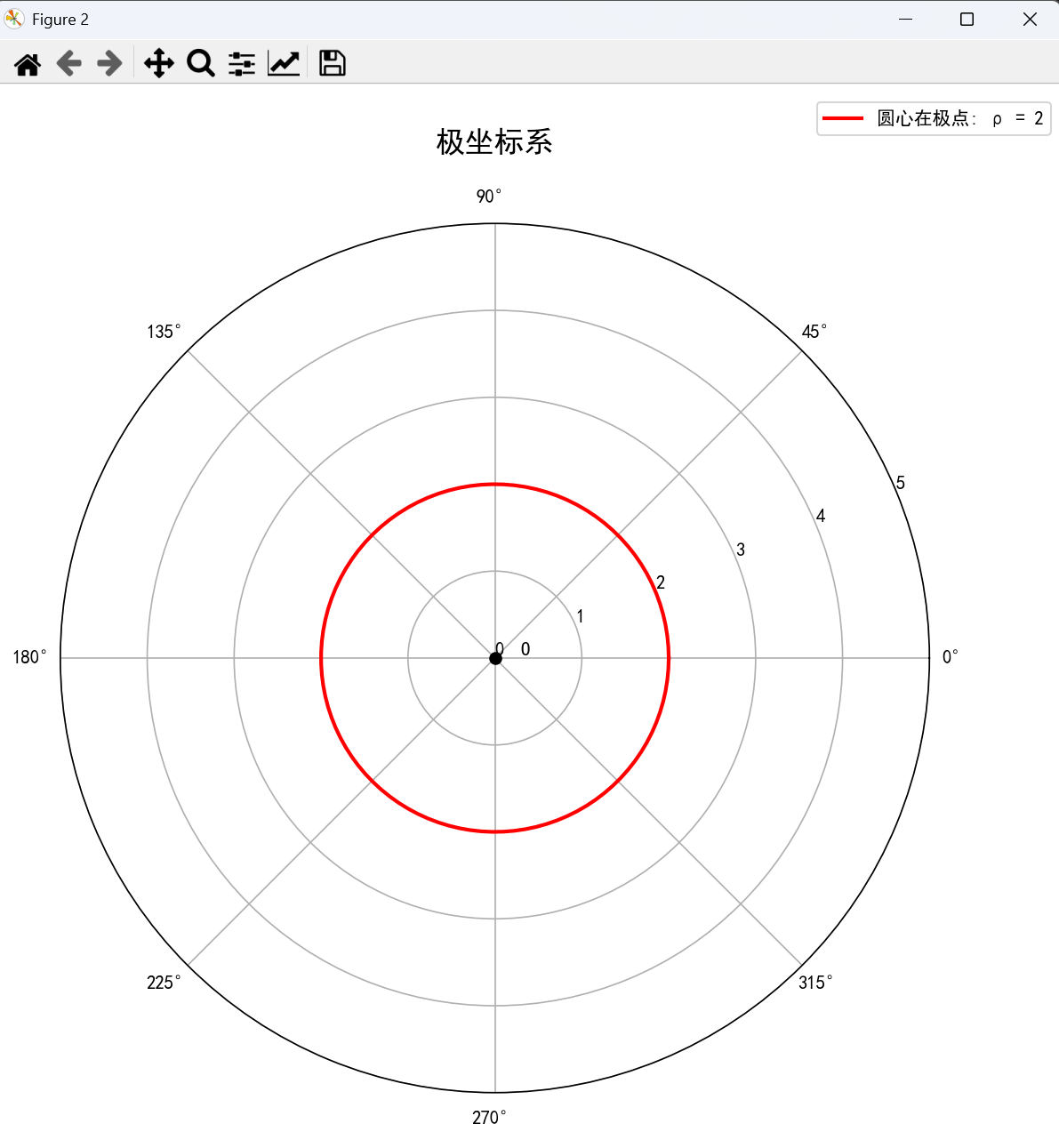
2. 圆的极坐标方程
圆心为 M(p0,θ0)M(p_0, \theta_0)M(p0,θ0) , 半径为 a 的圆的极坐标方程为:
p2−2p0pcos(θ−θ0)+p02−a2=0 p^2 - 2p_0p\cos(\theta - \theta_0) + p_0^2 - a^2 = 0 p2−2p0pcos(θ−θ0)+p02−a2=0
(1) 圆心在极点 p = a
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))# 圆心在极点的圆方程:ρ = R
theta = np.linspace(0, 2*np.pi, 100)
radius = 2
rho = np.full_like(theta, radius)
ax.plot(theta, rho, 'r-', linewidth=2, label=f'圆心在极点: ρ = {radius}')# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()
运行结果:
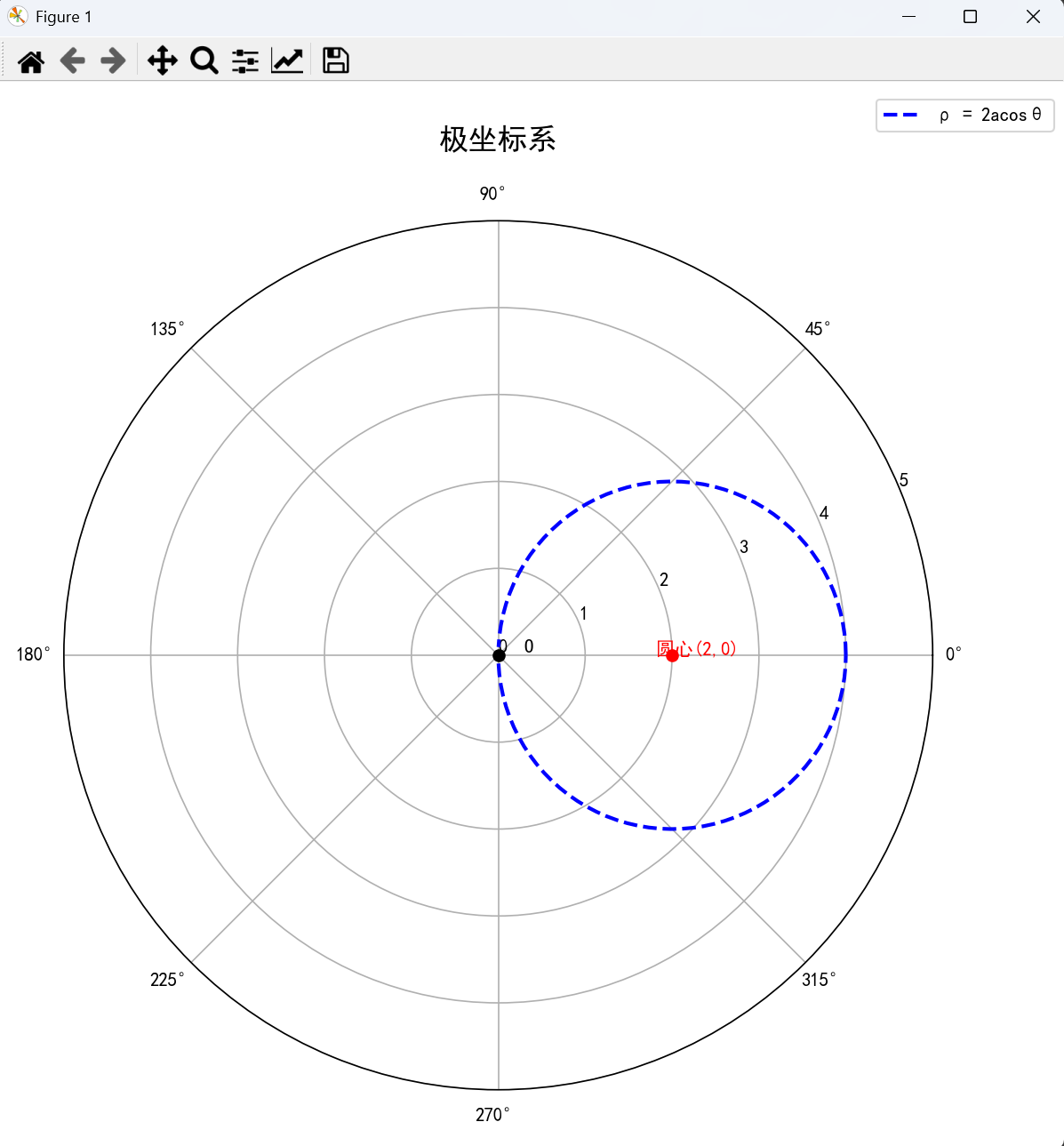
(2) 圆心在极点右侧 p=2acosθp=2a \cos \thetap=2acosθ
Python 代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 圆心在(a,0)的圆方程:ρ = 2acosθ
theta = np.linspace(0, 2*np.pi, 200)
a = 2
color = 'r'
# 计算ρ值:ρ = 2acos θ
rho_simplified = 2 * a * np.cos(theta)
# 绘制圆
ax.plot(theta, rho_simplified, 'b--', linewidth=2,label=f'ρ = 2acosθ')
# 标记圆心
ax.plot(0, a, color + 'o', markersize=6)
ax.text(0, a+0.3, f'圆心({a},0)', fontsize=10, color=color, ha='center')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()
运行结果:
(3) 圆心在极点上方 p=2asinθp = 2a\sin \thetap=2asinθ
Python 代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 圆心在(a,0)的圆方程:ρ = 2asinθ
theta = np.linspace(0, 2*np.pi, 200)
a = 2
color = 'r'
# 计算ρ值:ρ = 2asin θ
rho_simplified = 2 * a * np.sin(theta)
# 绘制圆
ax.plot(theta, rho_simplified, 'b--', linewidth=2,label=f'ρ = 2asinθ')
# 标记圆心位置 (0,a) - 在极坐标中对应(θ=π/2, ρ=a)
ax.plot(np.pi/2, a, color + 'o', markersize=6)
ax.text(np.pi/2, a+0.3, f'圆心(0,{a})', fontsize=10, color=color, ha='center')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()
运行结果:
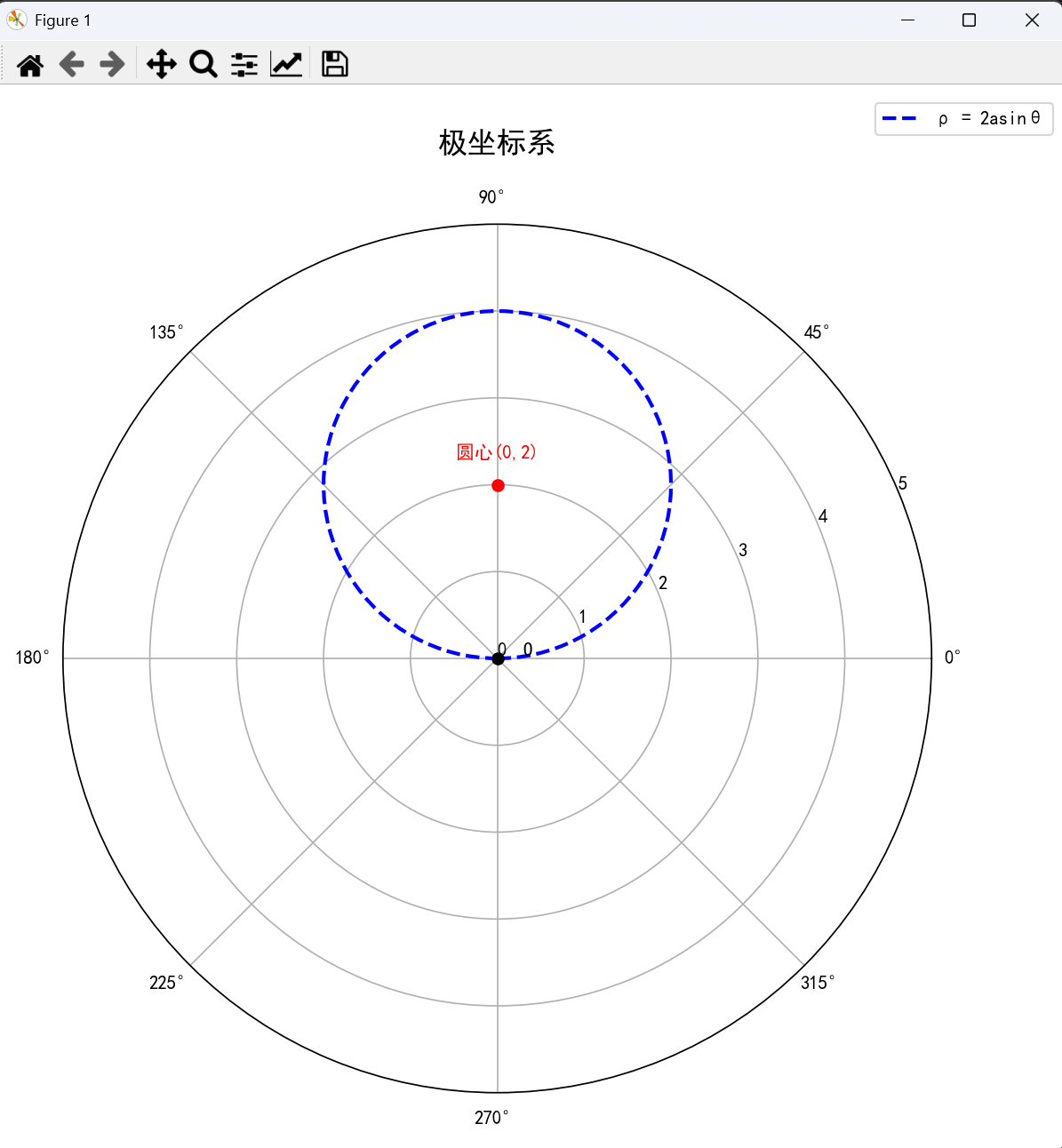
(4) 圆心在极点左侧 p=−2acosθp = -2a\cos \thetap=−2acosθ
Python 代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 圆心在(-a,0)的圆
theta = np.linspace(0, 2*np.pi, 200)
a = 2
color = 'r'
# 计算ρ值:ρ = -2acos θ
rho_simplified = -2 * a * np.cos(theta)
# 绘制圆
ax.plot(theta, rho_simplified, 'b--', linewidth=2,label=f'ρ = -2acosθ')
# 标记圆心位置 (-a,0) - 在极坐标中对应(θ=π, ρ=a)
ax.plot(np.pi, a, color + 'o', markersize=6)
ax.text(np.pi, a+0.3, f'圆心({-a}, 0)', fontsize=10, color=color, ha='center')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()
运行结果:
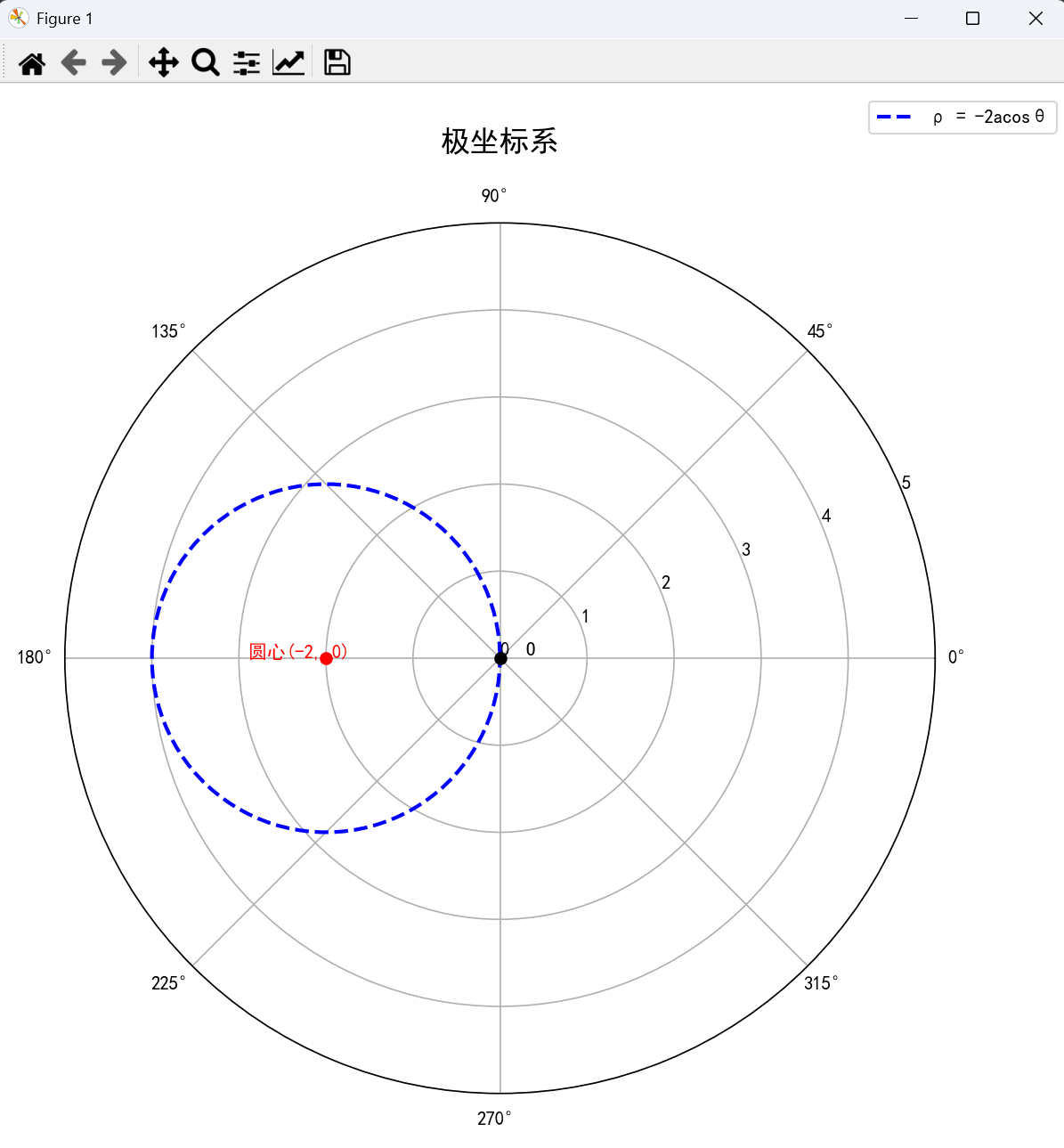
(5) 圆心在极点下方 p=−2asinθp=-2a\sin \thetap=−2asinθ
Python代码:
import matplotlib.pyplot as plt
import numpy as np
from test3 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 圆心在(0,-a)的圆方程:ρ = -2asinθ
theta = np.linspace(0, 2*np.pi, 200)
a = 2
color = 'r'
# 计算ρ值:ρ = -2asin θ
rho_simplified = -2 * a * np.sin(theta)
# 绘制圆
ax.plot(theta, rho_simplified, 'b--', linewidth=2,label=f'ρ = -2asinθ')
# 标记圆心位置 (0,-a) - 在极坐标中对应(θ=3π/2, ρ=a)
ax.plot(3*np.pi/2, a, color + 'o', markersize=6)
ax.text(3*np.pi/2, a+0.3, f'圆心(0,{-a})', fontsize=10, color=color, ha='center')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()
运行结果:
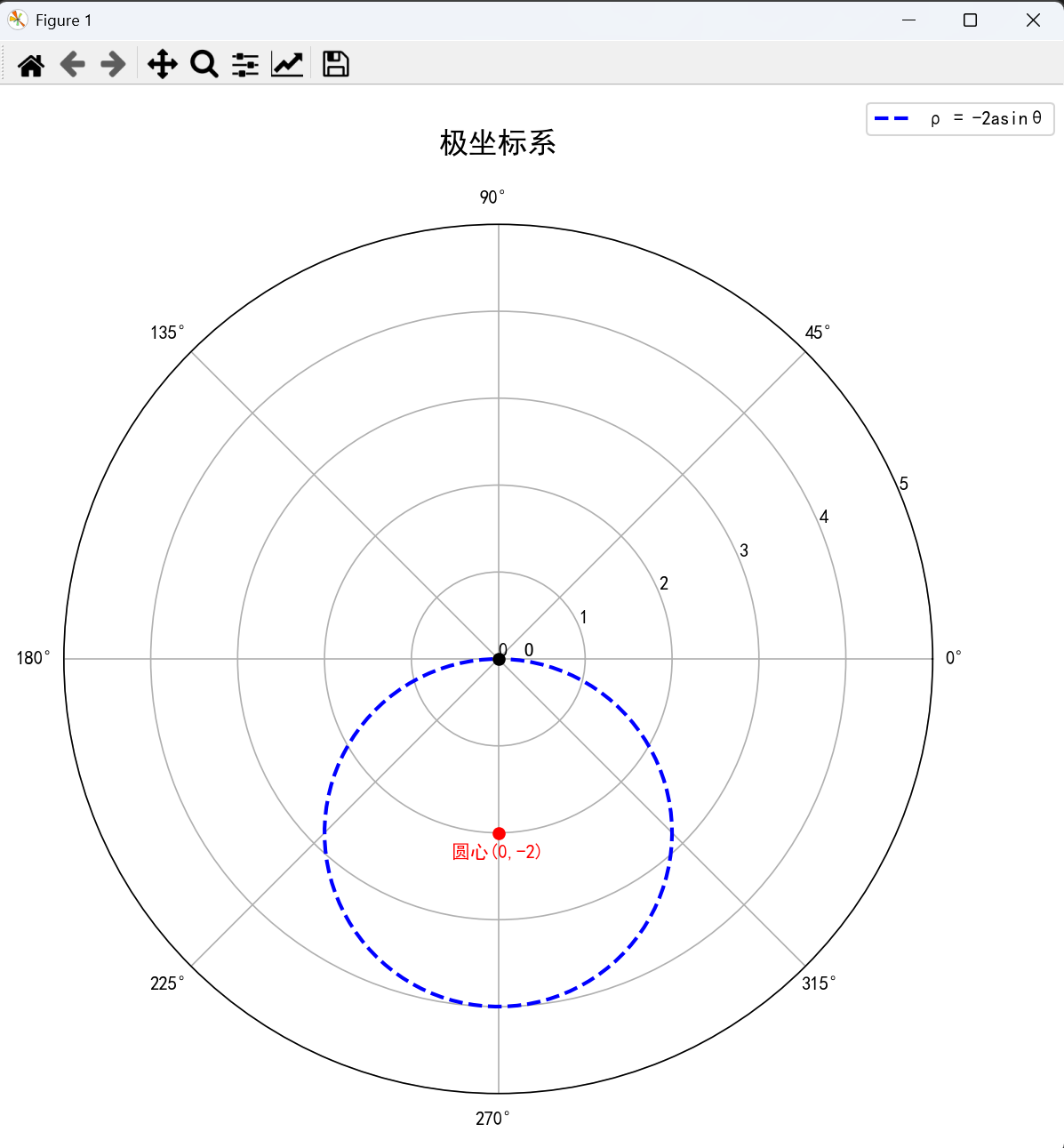
三、总结
后续我将继续使用Python实现扈志明《微积分》教材中的更多内容,包括极限、导数、积分等核心概念,通过编程实践深化对微积分知识的理解。
参考教材:扈志明,《微积分》,高等教育出版社。本文中的数学定义和概念均来源于此教材。
