贪心算法1

简介

1. 什么是贪心算法？
   贪心 = 鼠目寸光（形象描述 “局部最优” 的特点）。贪心算法的核心逻辑：将解决问题的过程拆分为多个子步骤，每一步都选择当前视角下的最优解，“希望” 通过局部最优推导全局最优。

2. 贪心算法的特点

• 贪心策略的提出没有固定模式，不同题目可能需要完全不同的贪心逻辑。
• 贪心策略的正确性需要严格证明（贪心可能是错误的方法，正确的贪心必须经过验证）。常用证明方法：数学中的各类证明手段（反证法、归纳法等）。

典型例子

• 例一：找零问题场景：用面值 [20, 10, 5, 1] 凑出 46，求最少硬币数。

证明：找零问题（贪心策略的正确性）
找零场景：用面值 [20, 10, 5, 1] 凑任意金额，贪心策略为 “每次选最大的可行面值”。
证明思路（反证法 + 最优解性质推导）：
1.定义最优解与贪心解：

• 设最优解的硬币组合为 [A, B, C, D]（A=20 的数量，B=10 的数量，C=5 的数量，D=1 的数量）。
• 设贪心解的硬币组合为 [a, b, c, d]（贪心策略：每次取最大可行面值，因此 a 是 “当前金额下最多能取的 20 数量”，b 是 “剩余金额下最多能取的 10 数量”，以此类推）。

2.分析最优解的性质：为了 “硬币数最少”，大面值应尽可能多取（否则用小面值凑会导致硬币数增加）。因此：

• B ≤ 1（若 B ≥ 2，则 2 个 10 可换成 1 个 20，硬币数更少，与 “最优” 矛盾）。
• C ≤ 1（2 个 5 可换成 1 个 10，硬币数更少）。
• D ≤ 4（5 个 1 可换成 1 个 5，硬币数更少）

3.对比贪心解与最优解：

• 对于 20 的数量 a 和 A：
  贪心取 20 元的数量 a 是 “当前最多能取的 20 元个数”，所以 a>=A
  再判断，如果a>A ，说明说明BCD能凑出至少1个A。结合前面B最大为1、…全部加起来才19。无法凑出A。所以a只能等于A。

同理可得B=b C=c，那最后的D肯定=d。

最终，贪心解和最优解的硬币组合完全一致，证明贪心策略正确。

860. 柠檬水找零

题目链接

分析：

//贪心策略：找零的时候先找10，再找5。确保手里有足够的零钱找零
//分析：1.根据题意，遍历完bills都能找零成功，返回true，如果存在不成功则返回false。
//2.可以通过一个哈希表去映射手中零钱的张数。
//3.一开始没有零钱的时候，如果收取的钱是10、20，直接返回false。

class Solution {
public:bool lemonadeChange(vector<int>& bills) {//贪心策略：找零的时候先找10，再找5。确保手里有足够的零钱找零//分析：1.根据题意，遍历完bills都能找零成功，返回true，如果存在不成功则返回false。//2.可以通过一个哈希表去映射手中零钱的张数。//3.一开始没有零钱的时候，如果收取的钱是10、20，直接返回false。unordered_map<int,int>hash;for(auto e:bills){if(e==5)hash[e]++;else if(e==10){//找钱hash[e]++;if(hash[5])hash[5]--;else return false;}else{//收入20可以不用统计，因为不会找出去，用不到if(hash[10]&&hash[5])hash[10]--,hash[5]--;else if(!hash[10]&&hash[5]>=3)hash[5]-=3;else return false;}}return true;}
};

证明：

这道题主要的问题就是对10块、20块的找零问题。
对于10块，无论你怎么找，都是找出去5块，没什么区别。

主要是20块，你可以找出去10+5 或者5+5+5。但是吧，10块只能是针对20时找出，5块可以对10、20找。通用性更强。所以从感觉上很好判断最优解肯定是针对20找10的策略。

定义 “最优解” 与 “贪心解” 的差异
假设存在一个最优解（能成功找零的零钱使用序列），其中处理某张 20 元 时，没有优先使用 10 元找零（即：明明有 10 元，却用了 3 张 5 元找零）。

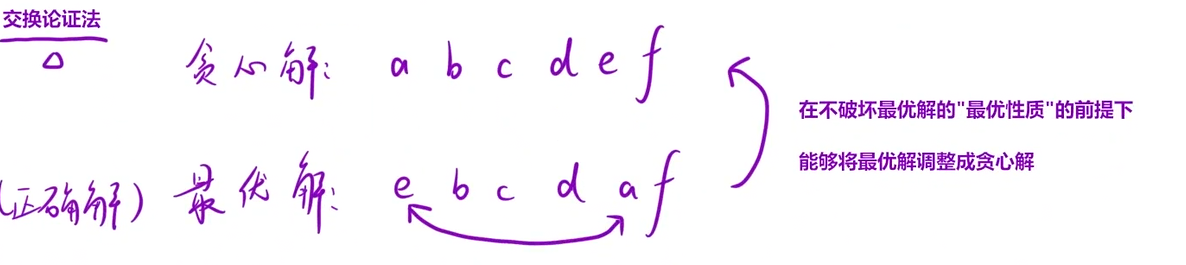
交换操作与可行性分析
对于上述 “非贪心” 的最优解，我们对「处理该 20 元」的步骤进行交换：

• 原操作：用 3 张 5 元 找零 → 消耗 five -= 3。
• 交换后操作：用 1 张 10 元 + 1 张 5 元 找零 → 消耗 ten -= 1, five -= 1。
  交换后，找零的总价值不变（都是 15 元），且：
• 5 元的剩余量：交换后比交换前 多 2 张（原消耗 3 张，现消耗 1 张）。
• 10 元的剩余量：交换后比交换前 少 1 张。

交换对后续的影响
由于 5 元的 “通用性更强”（可用于 10 元、20 元的找零），而 10 元 “仅能用于 20 元的找零”，因此：

• 交换后，5 元剩余更多 → 后续遇到 10 元顾客（需要 1 张 5 元找零）时，更不容易因 5 元不足而失败。
• 10 元仅减少 1 张 → 对后续 20 元顾客的影响很小（若后续有 20 元顾客，仍可优先用剩余 10 元找零）。

结论
通过交换，“非贪心的最优解” 可被转化为 “贪心解”，且转化后的解不会降低找零可行性（甚至更优）。因此，贪心策略是正确的 —— 它能覆盖所有可行的找零场景，且是最优策略的一种。

2208. 将数组和减半的最少操作次数

题目链接

根据题意：将数组和减半的最小操作次数。

贪心策略：很好想，每次把数组中最大的数减半就好了。
—》然后就转换到了找到数组中最大的数。
可以将数组的元素（包括减半后的数）全部放到一个大根堆里，每次取堆顶即可

class Solution {
public:int halveArray(vector<int>& nums) {priority_queue<double>heap;double sum=0;for(auto e:nums){sum+=e;heap.push(e);}int res=0;double count=0;while(count<sum/2){double x= heap.top();heap.pop();x/=2;count+=x;heap.push(x);res++;}return res;}
};

证明：
和上一题类似，交换论证法。
这种简单题的论证其实和推理的过程差不多。

因为我们的贪心解是每次找最大，然后减半。（单个最大的减半对整体减半的效率是最高的，找不出反证）

179. 最大数

题目链接

题意：排序，把数组排成最大的数
分析：
排序规则：第一位数较大的排前面（第一位数相同看第二位…以此类推）确保高位的数是最大的。—》总体就是最大的

思路：把数据转化成字符串然后按照字典序比较（按 “字符 / 元素顺序逐个比较”）

这里的贪心策略就是排序策略。

还有两个特殊情况处理，放代码注释里了

class Solution {
public:string largestNumber(vector<int>& nums) {int n=nums.size();vector<string>ret(n);int i=0;for(auto e:nums)ret[i++]=to_string(e);sort(ret.begin(),ret.end(),[](string& a,string& b){return (a+b)>(b+a);});//(a+b)>(b+a)确保拼接后更大，如330>303string res;//特殊情况处理，如果多个0拼接，结果返回0if(ret[0]=="0")return "0";for(auto s:ret)res+=s;return res;}
};

证明

1. 明确贪心策略
   对于任意两个数字字符串 a 和 b，若 a+b 的字典序 大于 b+a，则 a 应排在 b 前面（即 a 比 b 更 “适合” 靠前）。目标是证明：按此规则排序后，所有字符串拼接的结果是 “最大可能的数”。
2. 证明核心：比较规则满足 “全序关系”
   排序的前提是比较规则必须是 “全序关系”（能严格定义元素的先后顺序，且无矛盾），需满足 3 个性质：

（1）完全性
对任意两个字符串 a 和 b，a+b 与 b+a 的字典序一定可比较：

• 要么 a+b > b+a（a 在前），
• 要么 a+b < b+a（b 在前），
• 要么 a+b = b+a（顺序不影响结果）。
  因字符串的字典序比较是 “确定的”（逐字符比较，直到分出大小），故完全性成立。

（2）反对称性
若 a+b ≥ b+a 且 b+a ≥ a+b，则 a+b = b+a。此时 a 和 b 谁前谁后，拼接结果完全相同（例如 a=“22”, b=“2”，a+b=“222” 与 b+a=“222” 相等），故 “顺序无关”，满足反对称性。

（3）传递性（最关键）
需证明：若 a 应在 b 前（a+b ≥ b+a），且 b 应在 c 前（b+c ≥ c+b），则 a 一定应在 c 前（a+c ≥ c+a）。
转化为数值推导：设 a 的数值为 A（如 “3” 对应 3），长度为 len_a（如 “3” 长度为 1），则 a+b 的数值为 A×10^len_b + B（B 是 b 的数值，len_b 是 b 的长度）。

• 由 a+b ≥ b+a 得：A×10^len_b + B ≥ B×10^len_a + A，整理为：A×(10^len_b - 1) ≥ B×(10^len_a - 1) （式①）
• 由 b+c ≥ c+b 得：B×10^len_c + C ≥ C×10^len_b + B，整理为：B×(10^len_c - 1) ≥ C×(10^len_b - 1) （式②）

将式①和式②两边分别相乘（因所有项均为正数，不等号方向不变）：A×B×(10^len_b - 1)×(10^len_c - 1) ≥ B×C×(10^len_a - 1)×(10^len_b - 1)
约去两边相同的正数项（B×(10^len_b - 1)），得：A×(10^len_c - 1) ≥ C×(10^len_a - 1)
整理后即为：A×10^len_c + C ≥ C×10^len_a + A，即 a+c ≥ c+a。因此，传递性成立。

376. 摆动序列

题目链接

题目需求是要找到最长的摆动序列。
我们的贪心策略就是：
1.确保选的点的前后是摆动的（先增后减/先减后增）
2.选的点要尽可能靠前（确保后续有更多的点够我们选择）

总结起来就是我们需要选这个摆动线段的波峰/波谷+首尾两个点

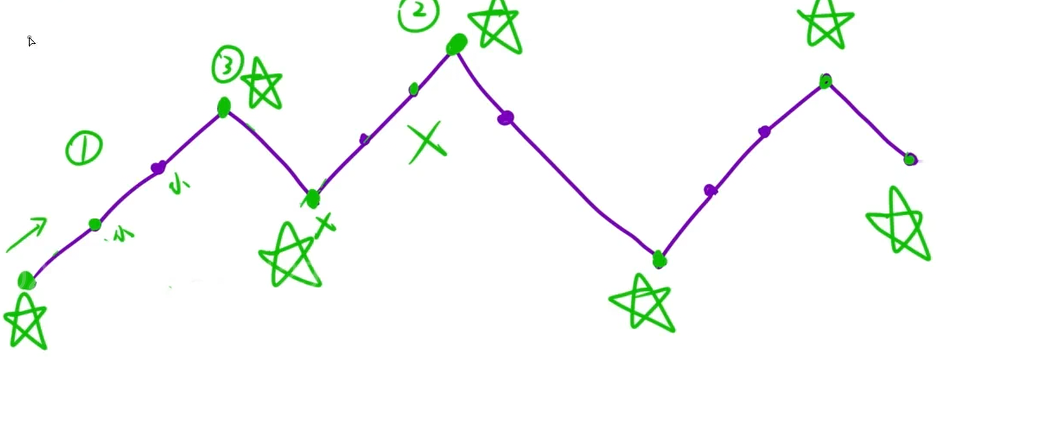
这里有几类特殊的情况：

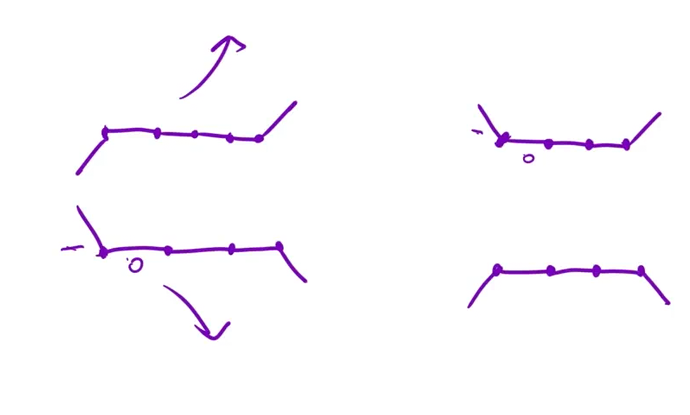
中间有部分的点是没有波动的，可以把这些平的（没有变化的）点去掉，左边就可以看作是递增/递减。右边就能看作是波谷/波峰。

接下来我们需要去判断什么时候是波峰/波谷：

很容易想到，如果是波峰。波谷 那么（右边-当前）*（当前-左边）<0。但是遇到中间是没有波动的特殊情况是无法判断的。如果我们把=0当作特殊情况省略，那特殊情况中的波峰/波谷也会被省略。

所以不能简单通过 点前后的数组差的乘积来判断。可以通过left 记录点左边的递增/递减状态（递增>0递减<0)right记录点 右边的状态。

然后遍历的时候，后续点的right继承前序点的left。如果遇到right=0，说明遇到没有波动的点，直接跳过即可。

一开始选择第一个点时无法确定左边的状态就取0.

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int res=0;int left=0,right=0;//统计波峰/波谷点for(int i=0;i<nums.size()-1;i++){right=nums[i+1]-nums[i];if(right==0)continue;if(right*left<=0)res++;left=right;//状态继承}res++;//最后一个点return res;}
};

证明：

用反证法证明 “贪心统计的峰谷数量就是最长摆动序列的长度”：
假设存在一个更长的摆动序列 T，其长度超过贪心策略统计的结果 S。

• 摆动序列的本质是 “趋势交替”：若序列中存在两个相邻的 “上升段”，中间必然需要一个 “下降段” 来衔接（反之亦然）。而 “峰”（上升转下降的点）和 “谷”（下降转上升的点）是趋势交替的核心节点。
• 若 T 比 S 长，说明 T 包含了一些 “非峰 / 谷” 的节点。但这些非极值点无法打破 “趋势交替” 的限制 —— 比如，两个峰之间的所有点，只有 “谷” 能让趋势从上升转下降；若用中间非谷的点替代谷，要么破坏趋势交替，要么无法延长序列。
• 因此，任何非峰 / 谷的节点都无法为摆动序列 “贡献新的交替”，最长序列的节点只能是峰或谷。

300. 最长递增子序列

题目链接

这题前面的动态规划有，下面贪心的思路是在动态规划的局限性上出发的。

原始 DP 解法中，定义 dp[i] 为以 nums[i] 结尾的最长递增子序列长度，状态转移为：(dp[i] = max(dp[j] + 1) (j < i 且nums[j] < nums[i]))

时间复杂度为 (O(n^2))

贪心优化的核心思想：“让子序列增长尽可能慢”
要得到最长的递增子序列，需让子序列的 “增长节奏尽可能慢”—— 即：对于相同长度的递增子序列，最后一个元素越小，后续元素就越容易满足 “递增” 条件，从而更可能延长子序列。
举个例子：长度为 3 的递增子序列，若末尾是 5，比末尾是 8 更优（后续只要遇到 >5 的元素就能延长，而 >8 的元素范围更小）。

定义辅助数组 tails
维护数组 tails，其中 tails[k] 表示：长度为 (k+1) 的递增子序列的最后一个元素的最小值。

举个例子：假设数组nums = [2, 5, 3, 7]，我们来看tails的构建过程：

• 长度为 1 的递增子序列：[2]、[5]、[3]、[7]，它们的最后一个元素是2,5,3,7，最小值是2 → 所以tails[0] = 2（k=0对应长度 1）。
• 长度为 2 的递增子序列：[2,5]、[2,3]、[2,7]、[5,7]、[3,7]，它们的最后一个元素是5,3,7,7,7，最小值是3 → 所以tails[1] = 3（k=1对应长度 2）。
• 长度为 3 的递增子序列：[2,5,7]、[2,3,7]，最后一个元素是7,7，最小值是7 → 所以tails[2] =7（k=2对应长度 3）。
  此时tails = [2,3,7]，显然是严格递增的。

tails的长度就是要求的最长递增子序列的长度。
由于tails是递增的，所以我们可以通过二分去优化求出tails的过程。让时间复杂度降低到N*logN

遍历 + 二分的执行逻辑
遍历原数组 nums 中的每个元素 num，用二分查找在 tails 中找到第一个 大于等于 num 的位置 pos，然后：

• 若 num 比 tails 中所有元素都大：说明 num 能延长当前最长的递增子序列，将 num 追加到 tails 末尾。
• 否则：用 num 替换 tails[pos]（让长度为 (pos+1) 的递增子序列的末尾元素更小，为后续元素留出更多 “延长空间”）。

最后返回tails的长度

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n=nums.size();vector<int>ret;ret.push_back(nums[0]);for(int i=1;i<n;i++){if(nums[i]>ret.back())ret.push_back(nums[i]);else{//二分int left=0,right=ret.size()-1;while(left<right){int mid=(left+right)>>1;if(ret[mid]<nums[i])left=mid+1;else right=mid;}ret[left]=nums[i];}}return ret.size();}
};