代码随想录 404.左叶子之和

注意：左叶子不是二叉树左侧节点，不能直接层序遍历。

1.什么是左叶子：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点。

2.左叶子之和举例：

（1）0，这棵树无左叶子。

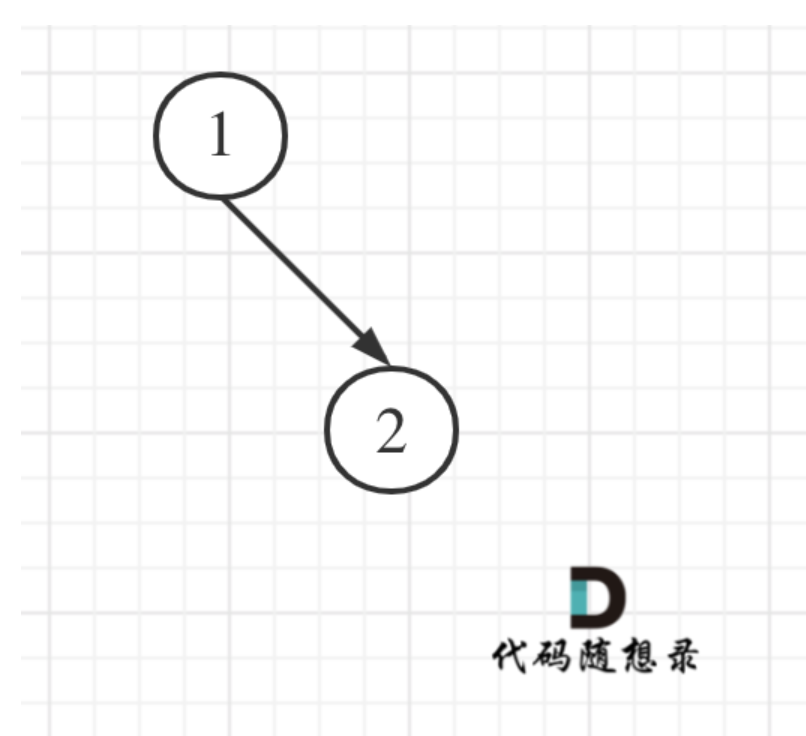
（2）左叶子之和为6+15=21。

3.判断当前节点是否为左叶子：需要借助该节点的父节点：如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子。判断代码如下：

if (root.left != null && root.left.left == null && root.left.right == null){
//左叶子节点处理逻辑
}

方法一：后序遍历（左右中）递归，因为要通过递归函数的返回值累加求取左叶子数值之和。

1.确定递归函数的参数和返回值：

（1）参数：树的根节点。

（2）返回值：返回数值之和，类型为int。

int sumOfLeftLeaves(TreeNode root) 

2.确定终止条件：

（1）如果遍历到空节点，那么左叶子值一定为0；

（2）如果遍历到叶子节点，那么其左叶子也一定为0（不写不影响结果）；

if (root == null) return 0;

3.确定单层递归的逻辑：当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和和右子树左叶子之和，相加便是整个树的左叶子之和。

        int leftValue = sumOfLeftLeaves(root.left);    // 左int rightValue = sumOfLeftLeaves(root.right);  // 右int midValue = 0;if (root.left != null && root.left.left == null && root.left.right == null) { midValue = root.left.val;}int sum = midValue + leftValue + rightValue;  // 中return sum;

附代码：

class Solution {public int sumOfLeftLeaves(TreeNode root) {if(root == null){return 0;}int leftValue = sumOfLeftLeaves(root.left);int rightValue = sumOfLeftLeaves(root.right);int midValue = 0;if(root.left != null &&root.left.left == null &&root.left.right == null){midValue = root.left.val;}int sum = midValue + leftValue + rightValue;return sum;}
}

方法二：层序遍历迭代法统计左叶子节点的数量。

附代码：

class Solution {public int sumOfLeftLeaves(TreeNode root) {LinkedList<TreeNode> queue = new LinkedList<>();if(root == null){return 0;}queue.add(root);int sum = 0;while(queue.size()>0){int size = queue.size();for(int i = 0;i<size;i++){TreeNode t = queue.remove();if(t.left != null){queue.add(t.left);if(t.left.left == null && t.left.right == null){sum += t.left.val;}}if(t.right != null){queue.add(t.right);}}}return sum;}
}