当前位置： 首页 > news >正文

《二叉树“防塌”指南：AVL 树如何用旋转 “稳住” 平衡？》

news 2025/10/20 8:12:30

目录

AVL树的结构

AVL树的插入

1.右单旋

2.左单旋，和右单旋类似

1.左右双旋

同理，右左双旋完全类似

检查这是不是AVL树

中序遍历

计算AVL树有多少个节点

find查找

普通的二叉搜索树BST没有平衡限制，可能退化成单支树，O（n），因此引入平衡二叉搜索树，效率变为O（log N）

AVL树：是一颗平衡的二叉搜索树。如果有左右子树的话，它的左右子树也是AVL树，且左右子树的高度差不为不超过1，通过控制高度差来控制平衡。

那该如何控制？

引入了平衡因子，即右子树高度-左子树高度，即AVL树的任何一个节点的平衡因子为0/-1/+1

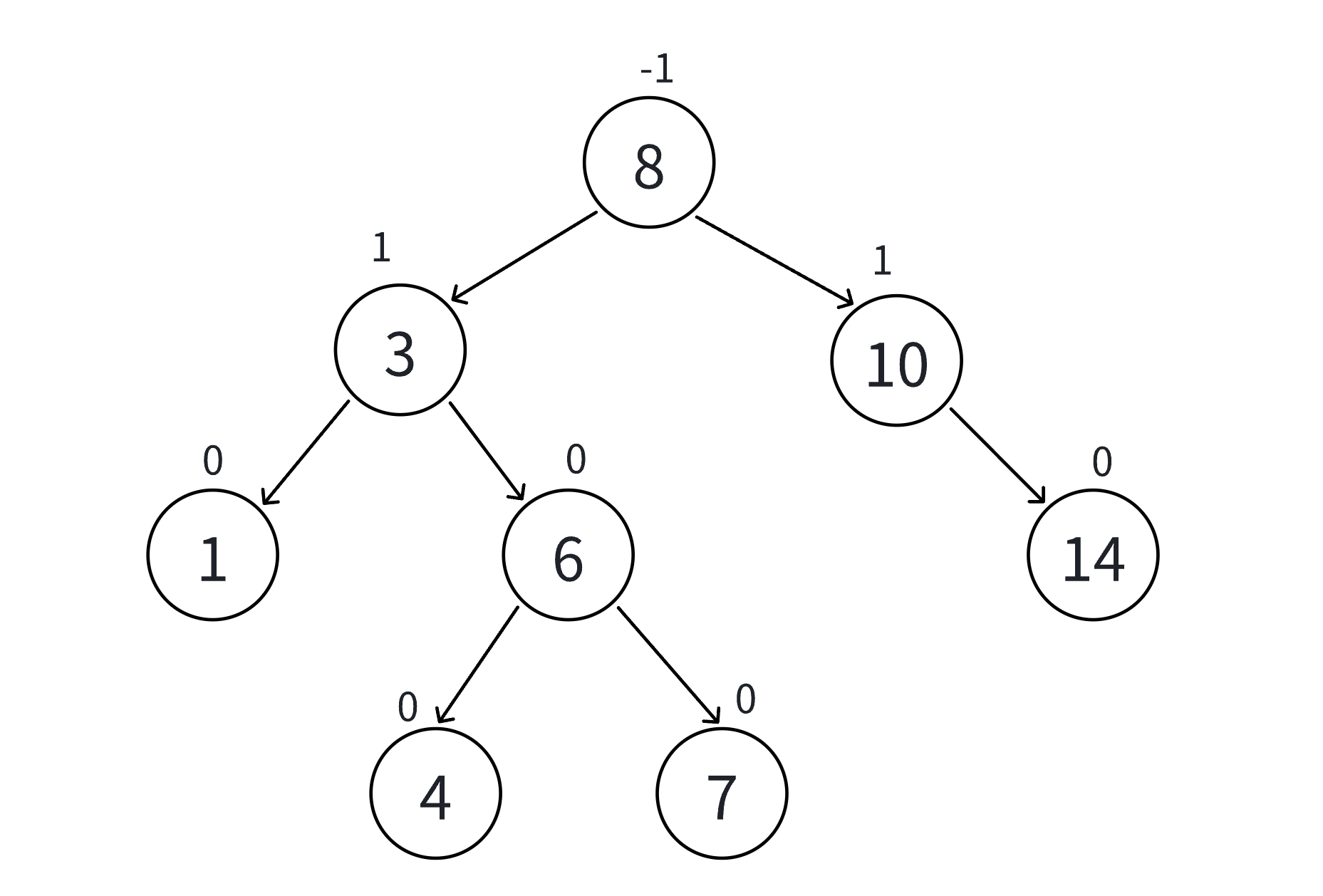
AVL树的结构

AVL是一个三叉链表，包括指向左孩子的节点指针，右孩子指针，parent指针（方便回溯），并引入平衡因子bf

template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;//节点存储的值int _bf;//平衡因子AVLTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){ }
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* _root = nullptr;
};

AVL树的插入

插入节点的步骤和二叉搜索树的插入类似，

首先要找到待插入的位置，判断子节点是插入到父节点的左边还是右边，将父节点与子节点进行链接，前面的大逻辑都差不多，这里直接给出前半部分的代码

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//此时找到待插入的位置了，parent的左节点/右节点cur = new Node(kv);if (parent->_kv.first < kv.first){//说明应该插入父亲的右边parent->_right = cur;}else{parent->_left = cur;}//新节点还要链接父亲cur->_parent = parent;//插入节点后还要更新平衡因子//begin
}

接下来是要更新平衡因子，更新平衡因子的时候可能出现不平衡，此时就要进行旋转

首先进行第一步，更新平衡因子：

平衡因子=右子树的高度-左子树的高度

更新平衡因子的原则：

如果新节点插入到父节点的左边，则父节点的平衡因子-1；如果新节点插入到父节点的右边，则父节点的平衡因子+1

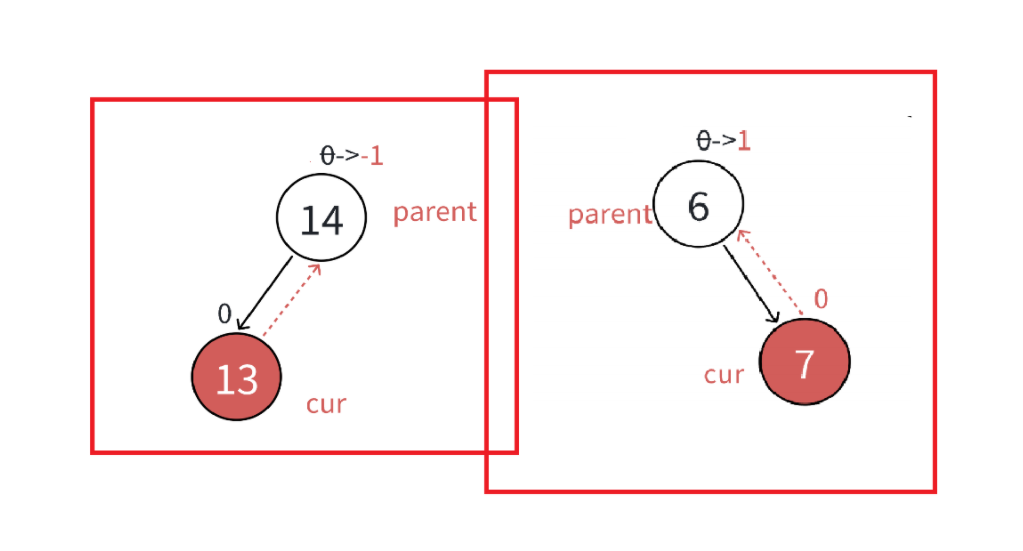
但插入一个节点不只是会影响父节点，也会影响祖先，因此还要判断parent子树的高度是否变化，parent子树高度的变化可以通过平衡因子的变化来判断

这里parent平衡因子的可能取值有三种 1/-1，0，2/-2

1.当更新后parent的平衡因子为1/-1时，则parent的平衡因子变化过程为：0->1/2->1（不可能，因为插入之前parent是平衡树，不存在平衡因子是2的情况），0->-1/-2->-1（不可能，因为插入之前parent是平衡树，不存在平衡因子是-2的情况），因此插入之前parent两边子树一样高，插入之后parent两边子树高度差为1，parent树符合平衡要求，但是高度增加了1，要向上面更新。

2.当更新后parent的平衡因子为2/-2时，则parent的平衡因子变化过程为：-1->-2/-3->-2（不可能，因为插入之前parent是平衡树，不存在平衡因子是-3的情况），1->2/3->2（不可能，因为插入之前parent是平衡树，不存在平衡因子是3的情况），因此插入之前parent两边子树高度差为1，插入之后parent两边子树高度差为2，parent树不符合平衡要求，需要旋转处理。不需要向上更新节点，也是更新结束条件，等下详细来讲。

3.当更新后parent的平衡因子为0时，则parent的平衡因子变化过程为：1->0/-1->0，说明插入之前parent高度差为1，新节点插在低的那边，插入后parent高度不变，不会影响到上层，更新结束。

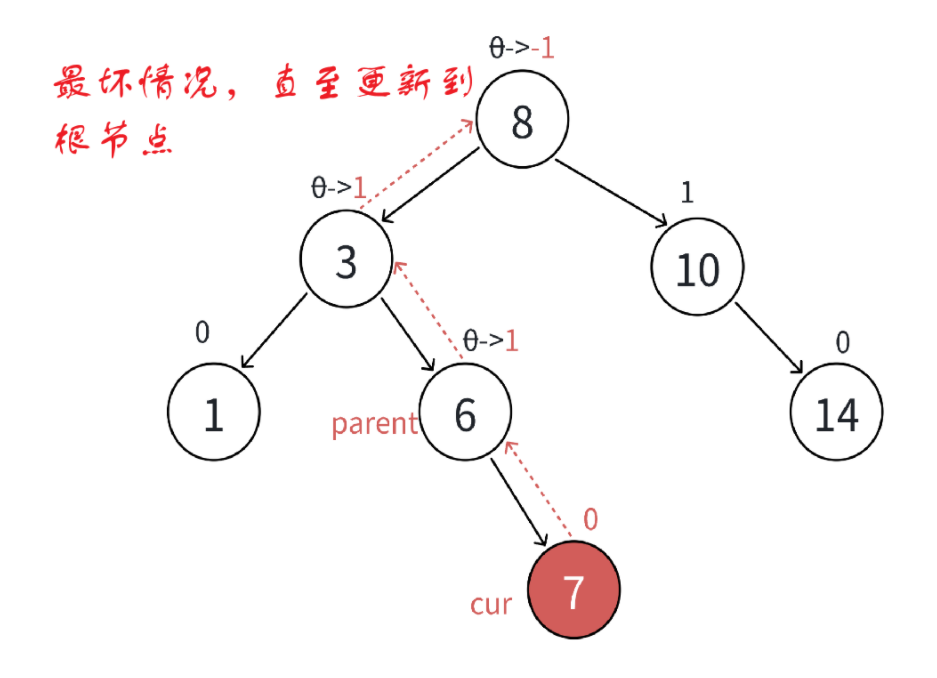
还有一种特殊境况，就是更新后parent的平衡因子永不为0，一直更新，到根节点也就停止了，这也是更新的结束条件。

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//此时找到待插入的位置了，parent的左节点/右节点cur = new Node(kv);if (parent->_kv.first < kv.first){//说明应该插入父亲的右边parent->_right = cur;}else{parent->_left = cur;}//新节点还要链接父亲cur->_parent = parent;//插入节点后还要更新平衡因子//beginwhile (parent)//到根节点，更新结束{//判断新节点插入到父亲的左/右if (cur == parent->_left)parent->_bf--;elseparent->_bf++;//平衡因子为0，更新结束if (parent->_bf == 0){break;//直接跳出循环}else if (parent->_bf == 1 || parent->_bf == -1){//继续向上更新cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//进行旋转//beginbreak;//旋转过后高度恢复到没插入的状态，不向上更新，更新结束跳出循环}else{assert(false);}}return true;
}

再进行第二步，parent树不符合平衡要求，需要进行旋转处理

旋转的两个目标：1.让parent树平衡，2.让parent的平衡因子恢复到插入节点之前的状态，即插入后高度不变，不会影响到上层祖先，也就不用继续向上更新，这是更新的结束条件。

旋转分为四种，先来讲单旋

1.右单旋

左子树的左子树过高，A的左孩子是B，B的左孩子是C（C的存在导致B偏高，进而导致A失衡），即同方向失衡

左边高，需要向右旋转，把左子树的高度压低

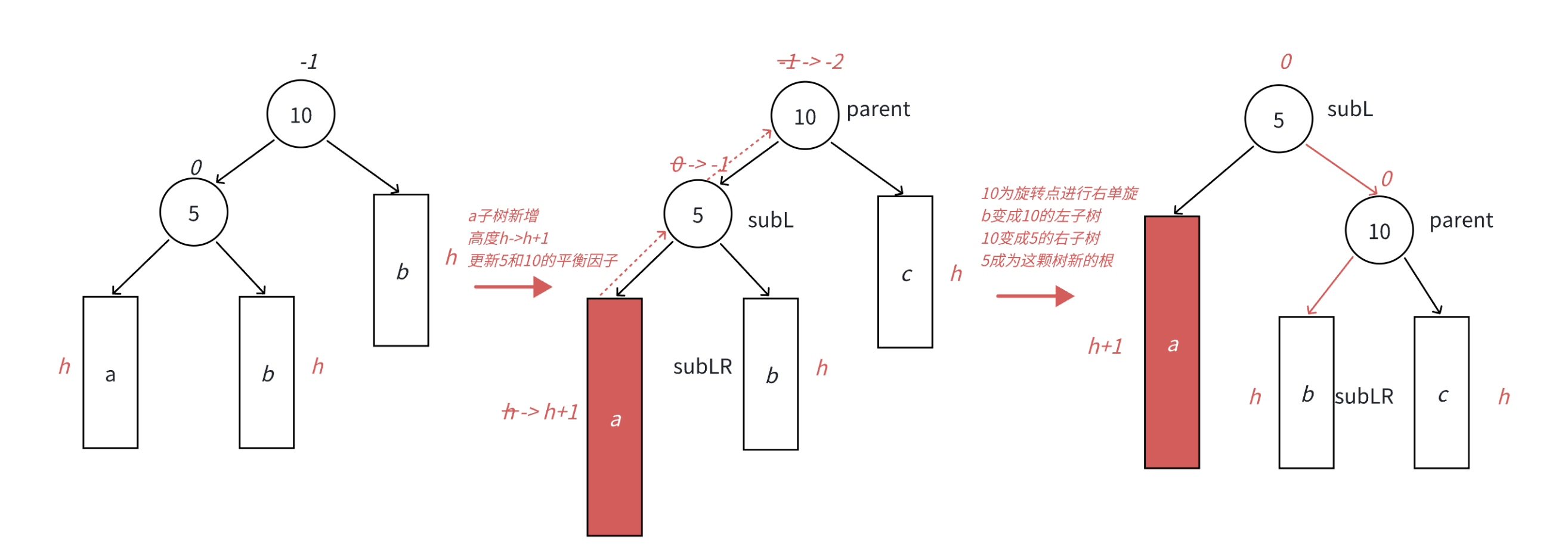
过程：5 < b < 10，将 b 链接到10的左子树，将10链接到5的右子树

关注两个节点，subLR和subL

首先更改suLR的父节点，subLR接到parent的左节点；同时也要将parent的左节点更改为subLR（parent->left=subLR;subLR->_parent=parent;）

接着更改subL的右节点，将subL的右节点链接parent；同时也要更改parent的父节点，更改为subL（subL->right=parent;parent->_parent=subL;）

以及parent已经不是parent->_parent的孩子了，parent->_parent要改变指向，此时就要判断parent是parent->_parent的左孩子还是右孩子，然后改变parent父节点指向的左/右孩子，更改为subL(parent->_parent->_left/_right=subL)。

要注意一下parent有没有父节点，以及进行->访问时，此节点是不是nullptr

//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;//b链接到10的左子树parent->_left = subLR;if(subLR)//前提是subLR！=nullptr//更改subLR的父亲subLR->_parent = parent;//记录一下parent->_parentNode* pparent = parent->_parent;//10链接到5的右子树subL->_right = parent;parent->_parent = subL;//parent的父节点也得指向新的孩子//parent有两种情况，1.parent本身是根节点，没有父节点，不用改变父节点的指向,直接改变根节点//2.parent不是根节点，改变父亲的指向parent->_parent->_left/_right=subLif (parent == _root){_root = subL;subL->_parent = nullptr;//改变subL的父节点}else{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}subL->_bf = 0;parent->_bf = 0;
}

2.左单旋，和右单旋类似

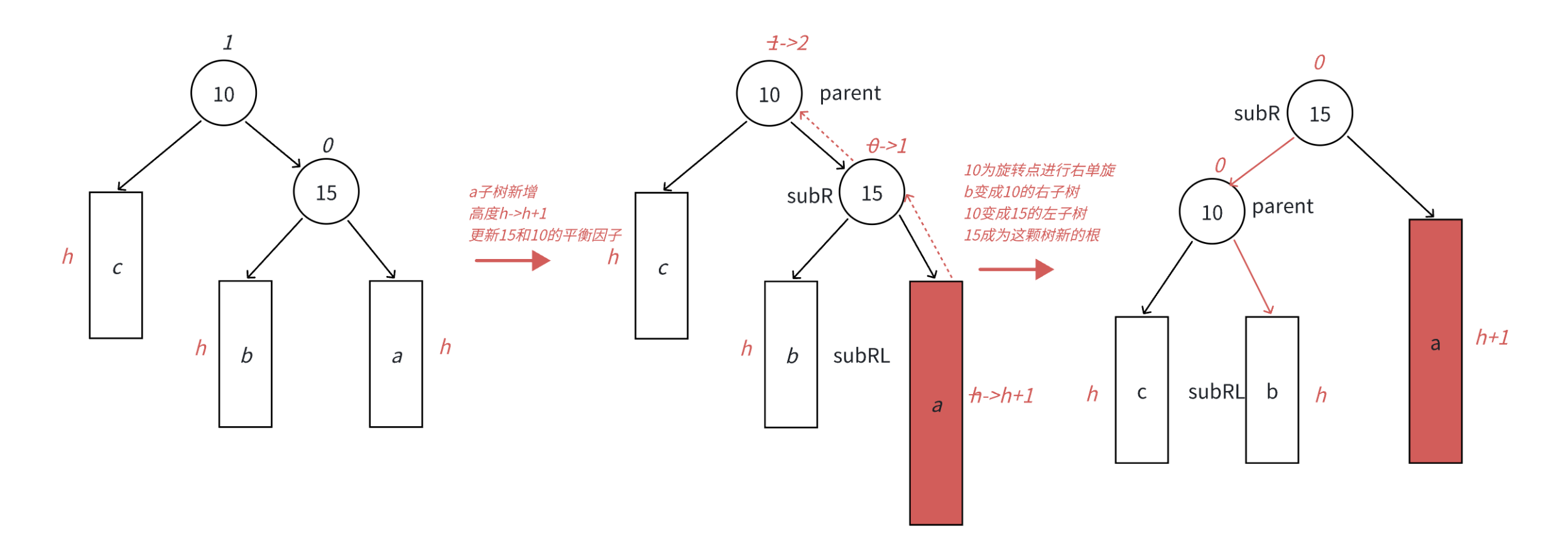
同理，是插入到右子树的右子树，即同方向失衡

过程：10 < b的值 < 15，将 b 链接到 10 的右子树，将 10 链接到 15 的左子树

关注两个节点：subRL 和 subR

parent->_right=subRL;subRL->_parent=parent;

subR->_left=parent;parent->_parent=subR;

还要注意两个节点的父亲指向，subR 和 parent 的父亲

如果parent不为root的话，parent->_parent的孩子已经改变，还要判断parent是parent->_parent的左/右孩子

 //左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//将b链接到10的右子树parent->_right = subRL;if(subRL)//前提subRL！=nullptr//更新b的父亲subRL->_parent = parent;//记录parent的父亲Node* pparent = parent->_parent;//将10链接到15的左边subR->_left = parent;//更新10的父亲parent->_parent = subR;//如果parent不为_root的话，要注意parent->_parent的孩子已经改变//如果parent为根的话，更新根if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}elsepparent->_right = subR;subR->_parent = pparent;}parent->_bf = 0;subR->_bf = 0;}

接下来是双旋，分两种情况

1.左右双旋

左子树的右子树过高，即A的左孩子是B，B的右孩子是C（C存在导致B偏高，进而A失衡）

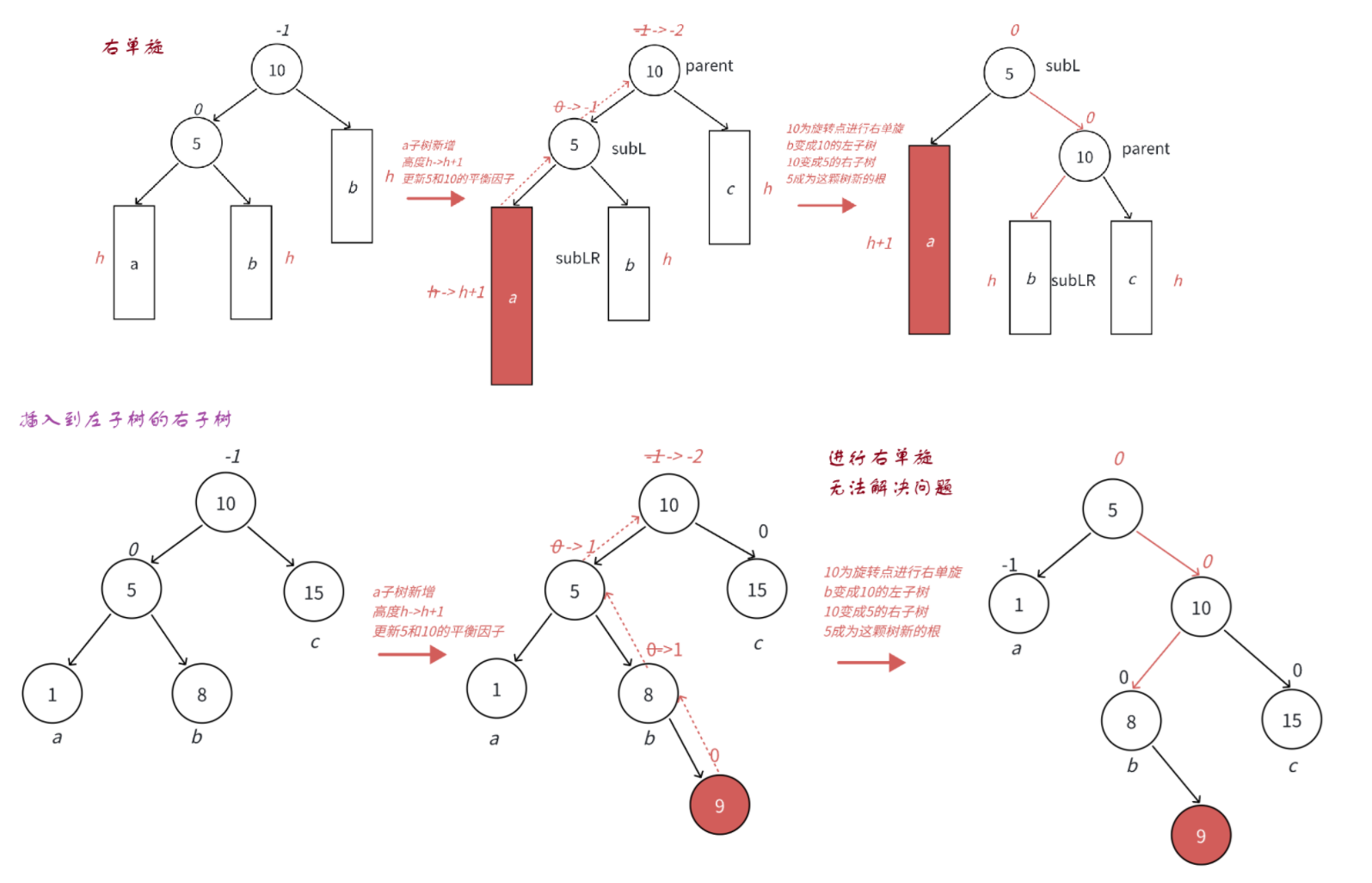
这种情况下单纯的右单旋/左单旋已经无法解决问题，需要旋转两次才能解决，先以 5 为节点进行左单旋，再以 10 为节点进行左单旋

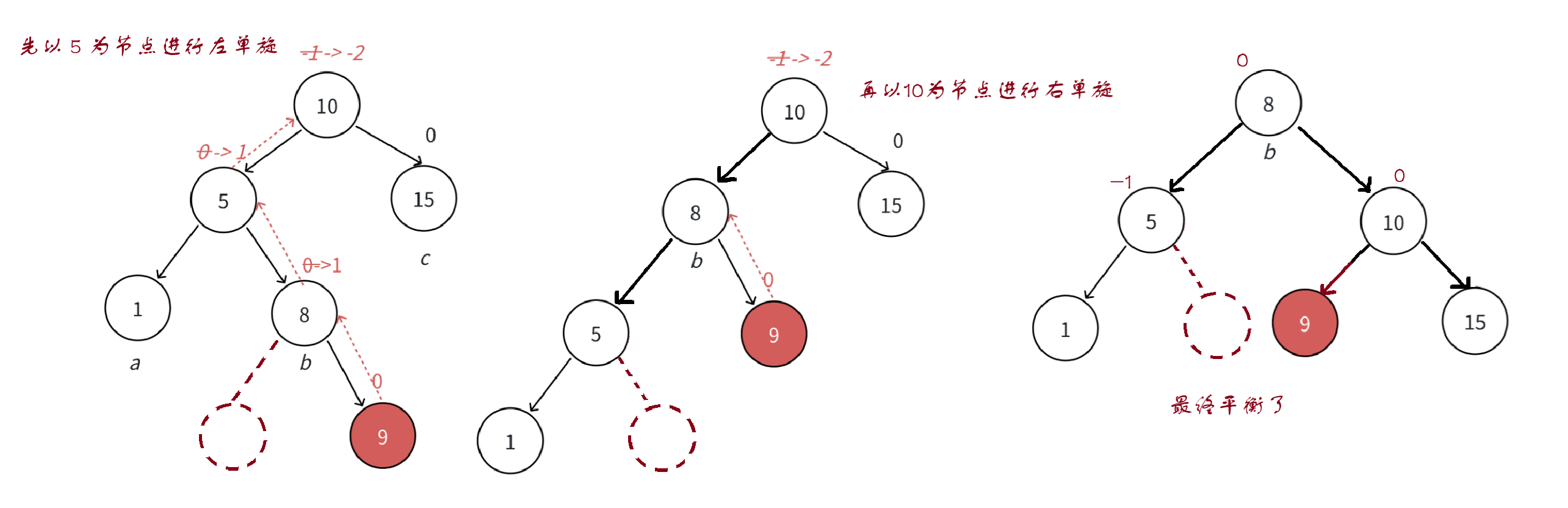
旋转的框架是这样的

 //左右双旋void RotareLR(Node* parent){Node* subL = parent->_left;Node* subLR == subL->_right;RotateL(subL);RotateR(parent);//更新平衡因子//begin}

但是我们要重写平衡因子的更新逻辑，单旋解决不了，都会搞成0

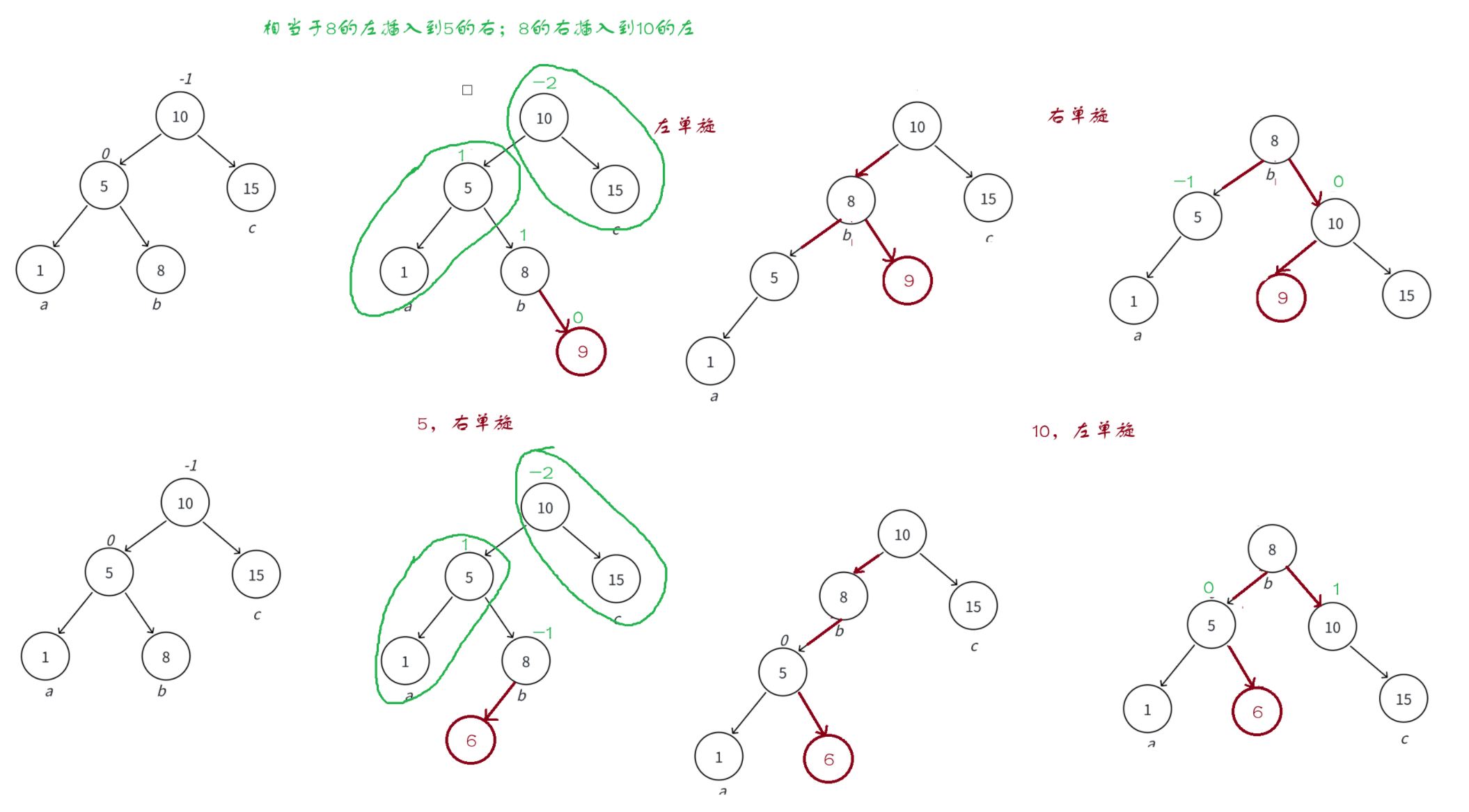
  • 可以分成3个块，看图
  • 8的左边分给了5的右边，8的右边分给了10的左边，8成为根节点

在8的左边和右边插入都会引发双旋，但是8的左右会分给5/10，这会导致平衡因子有差异

怎么区分是插入8的左边还是8的右边？看平衡因子

  • 8的平衡因子为1，在右边插入；为-1，左边插入
  • 8的平衡因子为0，自己就是新增

也就是3种情况

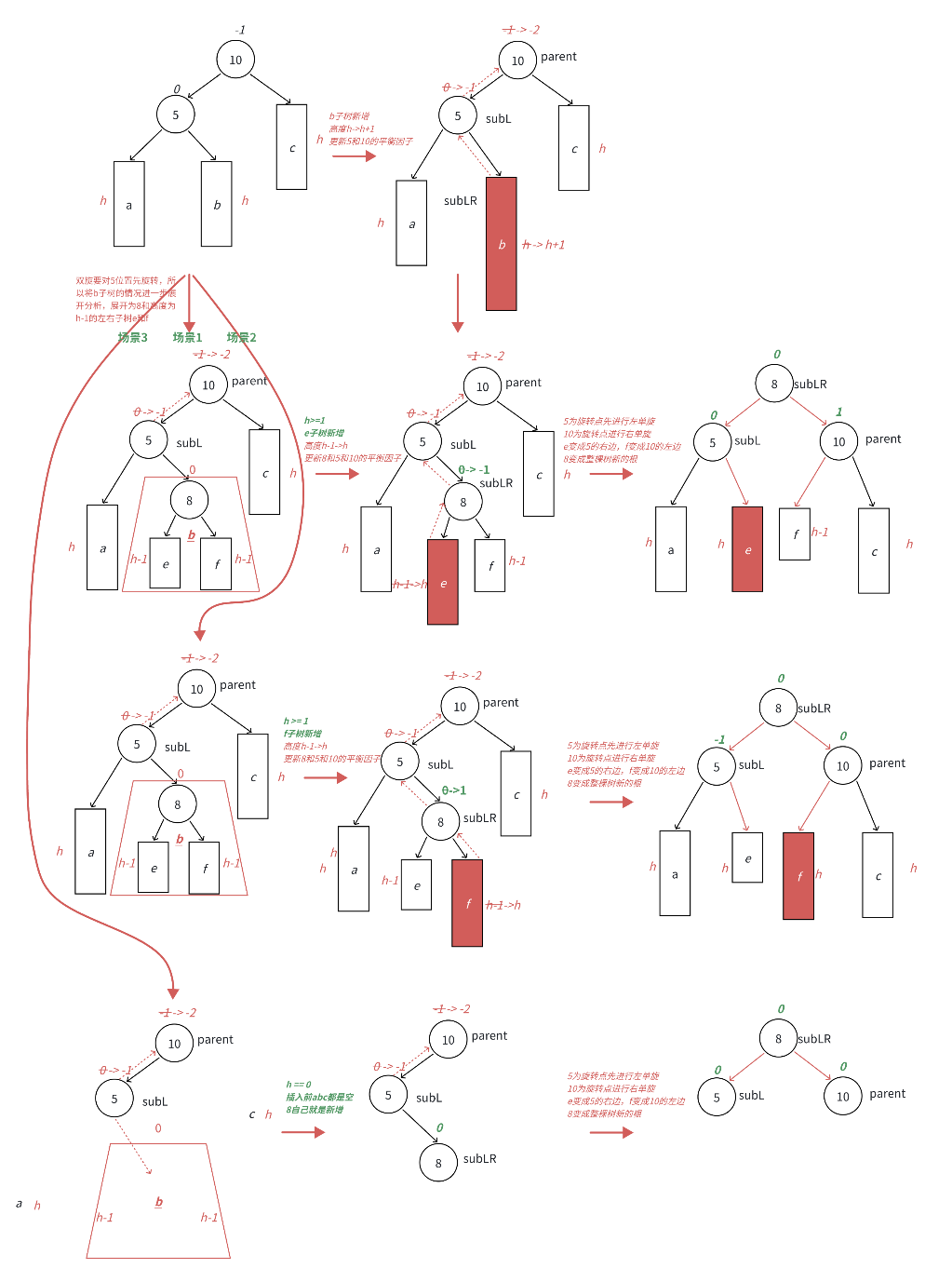
关注8的平衡因子

//左右双旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//提前保存RotateL(subL);RotateR(parent);//更新平衡因子//beginif (bf == 0)//8本身就是新插入节点{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 1)//在8的右边插入，8的左边给5；8的右边给10，平衡因子变-1{subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1)//在8的左边插入，8的右边给10，8的左边给5，平衡因子变1{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

同理，右左双旋完全类似

//右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//提前保存RotateR(subR);RotateL(parent);//接着调整平衡因子//插入到e子树if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

接着我们完善插入代码

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//此时找到待插入的位置了，parent的左节点/右节点cur = new Node(kv);if (parent->_kv.first < kv.first){//说明应该插入父亲的右边parent->_right = cur;}else{parent->_left = cur;}//新节点还要链接父亲cur->_parent = parent;//插入节点后还要更新平衡因子//beginwhile (parent)//到根节点，更新结束{//判断新节点插入到父亲的左/右if (cur == parent->_left)parent->_bf--;elseparent->_bf++;//平衡因子为0，更新结束if (parent->_bf == 0){break;//直接跳出循环}else if (parent->_bf == 1 || parent->_bf == -1){//继续向上更新cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//进行旋转//beginif (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}

检查这是不是AVL树

这里有两种方式，一是判断平衡因子是否合理，但这不科学，因为平衡因子有可能出错；二是通过高度判断，这个高度的代码相对简单，不易出错。

public:int Height(){return _Height(_root);}private:int _Height(Node* root){if (root == nullptr)return 0;int LeftHeight = _Height(root->_left);int RightHeight = _Height(root->_right);int MaxHeight = max(LeftHeight, RightHeight);return MaxHeight + 1;//加上本节点的高度}

接下来通过计算每一棵子树的高度差，来判断AVL是否是平衡树

public:bool IsBalanceTree(){_IsBalanceTree(_root);}private:bool _IsBalanceTree(Node* root){//递归结束条件if (root == nullptr)return true;int LeftHeight = _Height(root->_left);int RightHeight = _Height(root->_right);int diff = RightHeight - LeftHeight;//先判断根节点开始的树是一颗AVL树if (abs(diff) >= 2)//不符合平衡树的规则{cout << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << "平衡因子异常" << endl;return false;}//再判断左右子树都是一颗AVL树；如果是，那这棵树一定是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}

中序遍历

public:void InOrder(){return _InOrder(_root);}
private:void _InOrder(Node* root){//递归结束条件        if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first <<":" << root->_kv.second << " ";_InOrder(root->_right);}

套一层，参数是_root，外部无法传入

计算AVL树有多少个节点

public:int size(){return _size(_root);}private:int _size(Node* root){//递归结束条件if (root == nullptr)return 0;int leftsize = _size(root->_left);int rightsize = _size(root->_right);return leftsize + rightsize + 1;}

find查找

//红黑树的查找
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first == key){return cur;}else if (cur->_kv.first < key){cur = cur->_right;}else{cur = cur->_left;}}return nullptr;
}

拜拜，下期再见~

http://www.dtcms.com/a/503270.html

相关文章：

  • 网站制作wap页面wordpress微信公众平台开发
  • 分解如何利用c++修复小程序的BUG
  • 若依微服务 nacos的配置文件
  • 63.【.NET8 实战--孢子记账--从单体到微服务--转向微服务】--新增功能--预算告警
  • 网站建设没有业务怎么办德州网架公司
  • 九成自动化备份知乎专栏
  • 圆形平面阵列与平面方形阵的导向矢量：原理与实现
  • Altium Designer（AD24）Help帮助功能总结
  • 网站建设 个人2012版本wordpress
  • 6.2 域名系统 (答案见原书 P271)
  • php怎么网站开发上海网站建设86215
  • C程序中的指针：动态内存、链表与函数指针
  • 免费注册网站软件2022推广app赚佣金平台
  • 【Linux运维实战】彻底修复 CVE-2011-5094 漏洞
  • Java | 基于redis实现分布式批量设置各个数据中心的服务器配置方案设计和代码实践
  • STM32中硬件I2C的时钟占空比
  • iFlutter --＞ Flutter 开发者 的 IntelliJ IDEA / Android Studio 插件
  • Easyx图形库应用（和lua结合使用）
  • 网站建设计划表模板网络运营需要学什么专业
  • Scrapy 框架入门：高效搭建爬虫项目
  • 【JVM】详解 垃圾回收
  • 【前端魔法】实现网站一键切换主题
  • 电子 东莞网站建设wordpress 图片服务器配置
  • Spring Boot 3零基础教程，WEB 开发 通过配置类代码方式修改静态资源配置 笔记31
  • Vue模块与组件、模块化与组件化
  • SiriKali，一款跨平台的加密文件管理器
  • 构建优雅的 Spring Boot Starter：深入掌握国际化与配置覆盖的最佳实践
  • 网站建设的意义单页式网站
  • 易申建设网站兼职做ps网站
  • 力扣（LeetCode) ——11.盛水最多的容器（C++）