经典排序算法的实现与解析
目录
- 1.直接排序
- 2.希尔排序
- 3.选择排序
- 4.快速排序
- 4.1 Koare方法
- 4.2 挖坑法
- 4.3 快慢双指针
- 4.4 栈实现快速排序
- 4.5 时间消耗
- 4.6 快速排序的优化
- 5.归并排序
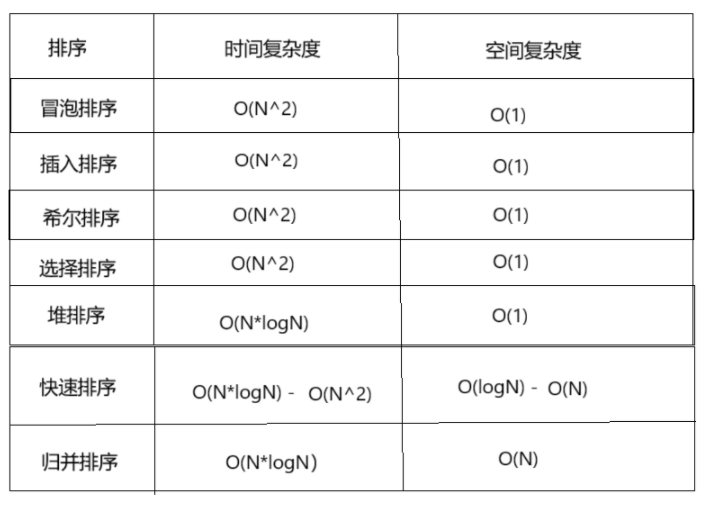
- 6.常见排序的时空复杂度
1.直接排序
直接插入插入排序是在已经有序的数据中找到合适位置进行插入,完成数据的排序。例如在数组【1,2,4】中插入元素 3,元素首先与4比较,4 大于 3 ,将 4 与 3 的位置进行交换,再与元素 2比较,3 大于 2,完成插入。
例子: 给定数组【5,3,1,6,7,2,4】,使用直接插入排序完成升序排序。
实现方式:定义变量i,i 从0下标开始遍历数组,将i下标的元素与前面当元素比较,选择合适位置插入,直到数组遍历完成,数组此时就是有序的。
0下标位置前没有元素,元素5存放在0下标

i = 1,元素3小于元素5,将i下标与i - 1下标交换,i–,此时i = 0,前面没有元素,元素3存放在0下标,完成【0,1】区间的排序。

以此类推,每插入一个元素,排序的区间就加一,当 数组末尾下标的元素完成插入时,就完成了【0,length - 1] 区间的排序。

public void insertSort(int[] arr){//1.定义变量i,遍历数组int i = 0;for(;i < arr.length;i++){//2.此时还需要定义一个变量j,完成【0,j】区间排序//因为是从后往前插入元素,需要考虑边界情况,j下标的元素//与前面的元素可交换的条件为 j > 0//j = 0 时,j 下标前面没有元素不可交换int j = i;while(j > 0){//j 下标的元素小于 j - 1 下标的元素if(arr[j] < arr[j - 1]){int tem = arr[j];arr[j] = arr[j - 1];arr[j - 1] = tem;//交换后j下标往前移j--;}//如果已经有序,不需要交换,跳出循环else break;}}}
public static void main(String[] args) {Solution s = new Solution();int[] arr = {5,3,1,6,7,2,4};s.insertSort(arr);for(int x : arr) System.out.print(x + " ");}

直接插入排序时间复杂度:O(N^2)当排序的元素是降序的,遍历第一个元素比较的次数为0,第二个元素元素的比较次数是1,
到第n个元素的比较次数为n - 1,将所有次数相加得到 (n - 1)/ 2 -》 O(n)空间复杂度:O(1) 在原数组上排序,不需要额外的空间消耗
2.希尔排序
希尔排序又称增量减少排序,排序的思想是通过分组将元素在指定组中进行元素的交换,分组的实现通常是通过数组的长度除以 2 获取第一次的组gap,之后的分组在当前的分组基础上除以2获取新的分组,直到最后的gap为1,完成最后一次分组。
例子:给定一个数组 nums[ 2,1,77,44,20,11,66,33,222],通过希尔排序把数组的元素变为有序的。


//希尔排序public void shellSort(int[] arr){int len = arr.length;int gap = len / 2;while(gap >= 1){//两个一组 可以比较, gap = 0,只有一个元素比较不需要比较//i - i + gap 为一组的范围,排序规则 i 与 i+gap 下标比较for (int i = 0; gap + i < len; i++) {//左边大于右边元素就交换if(arr[i] > arr[gap + i]){int tem = arr[i];arr[i] = arr[gap + i];arr[gap + i] = tem;//回退:可能交换后的元素(此时i下标的元素)还可以按照//[(i - gap) - i] 的范围分组,比较一下两个下标的值//满足交换条件 就交换两数for(int j = i - gap; j >= 0;j -= gap){if(arr[j] > arr[j + gap]){tem = arr[j];arr[j] = arr[j + gap];arr[j + gap] = tem;}else break;//已经是有序的}}}gap /= 2;}}
public void shellSort1(int[] arr){int len = arr.length;int gap = len / 2;while(gap >= 1){for (int i = 0; gap + i < len; i++) {int tem = arr[gap + i];int j = i;//回退:如果j下标元素大于j + gap下标元素就覆盖for (; j >= 0 ; j-= gap) {if(arr[j] > tem)//是j与tem比较,不是与j + gap//下标元素比较,与直接插入排序的元素插入思想是一样的//将tem 插入到前面的有序序列arr[j + gap] = arr[i];else break;}//此时的j是小于0的,需要将i + gap位置的元素补齐arr[j + gap] = tem;}gap /= 2;}}
public static void main(String[] args) {Solution s = new Solution();int[] arr = {2,1,77,44,20,11,66,33,222};s.shellSort(arr);for(int x : arr) System.out.print(x + " ");}

比较直接插入排序与希尔排序进行排序需要花费的时间
public static void main(String[] args) {Solution s = new Solution();int[] arr = new int[10000];for(int i = 0;i < 10000;i++) arr[i] = 10000 - i;int[] arr1 = Arrays.copyOf(arr,arr.length);long s1 = System.currentTimeMillis();s.insertSort(arr);long e1 = System.currentTimeMillis();System.out.println("直接插入排序需要的时间:" + (e1 - s1));long s2 = System.currentTimeMillis();//当前系统时间的时间戳s.shellSort(arr1);long e2 = System.currentTimeMillis();//当前系统时间的时间戳System.out.println("希尔排序的时间:" + (e2 - s2));//计算差值,单位毫秒}
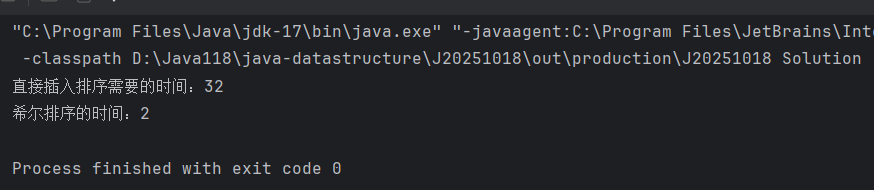
希尔排序时间复杂度:O(N^1.3 - N^1.5) 希尔排序的比较次数难以统计,时间复杂度是通过大量数据统计得出空间复杂度:O(1) 在原数组上排序,不需要消耗额外空间
3.选择排序
选择排序开始是选定一个值作为最大值或值最小值,将该元素与其他元素进行比较,最终确定一个最大值或者最小值,一层比较就可以确定一个数,通过多层比较就可以把元素全部排序。
例如:给定一个数组arr[3,77,2,2,66,80,102],将数组通过选择排序完成升序。

//选择排序public void selectSort(int[] arr){int length = arr.length;for(int i = 0;i < length - 1;i++){int minIndex = i;for(int j = i+ 1;j < length;j++){if(arr[j] < arr[minIndex])minIndex = j;}//交换int tem = arr[minIndex];arr[minIndex] = arr[i];arr[i] = tem;}}
public static void main(String[] args) {Solution s = new Solution();int[] arr = {3,77,2,2,66,80,102};s.selectSort(arr);for(int x : arr) System.out.print(x + " ");}

选择排序时间复杂度:O(N^2)
第一层排序比较的次数最多是length - 1,确定第一个数
第二层排序比较的次数最多是length - 2,确定第二个数
---
第n 层排序比较的次数最多是0,确定第最后一个数 T(n) = 0 + 1 + 2 + --- + length - 2 + length - 1 = (length - 1)length / 2 -> O(N^2)空间复杂度:O(1) 原数组上排序,不需要额外空间
4.快速排序
4.1 Koare方法
快速排序是选定一个基准值target,使排序元素中小于target值的位于左边,大于target值的位于右边,然后再将taget划分的左边区域和右边区域按照同样的方式重新选定一个新的基准值target划分各自的左右区间,直到排序完成。
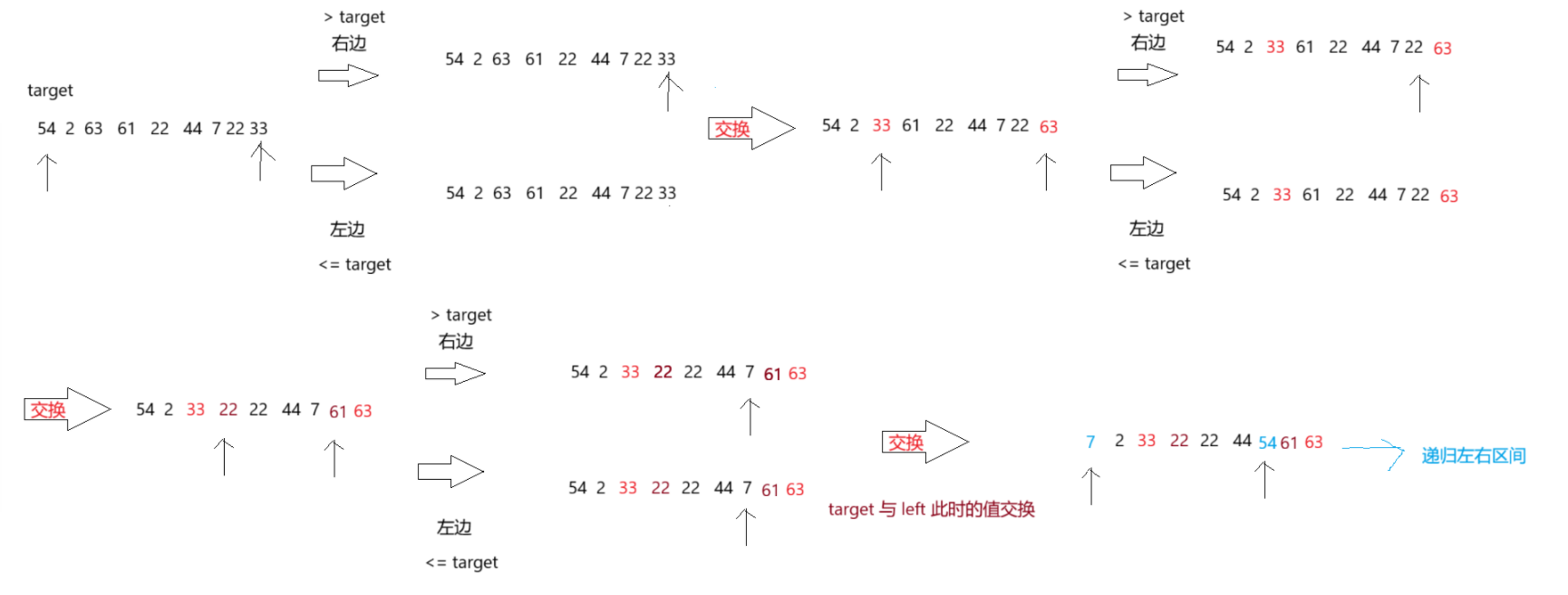
例子:给定一个数组arr[52,2,63,61,22,44,7,33],使用快速排序完成排序。
给定两个指针;left 和 right,开始left 赋值为0,right赋值为length - 1,从右边开始遍历数组,找到小于等于基准值的的元素,然后从左边开始遍历找到大于基准值的元素,左右区间都找到交换的元素,进行交换,重复上述过程,直到循环结束,最后交换基准值位置和left下标位置的元素,完成基准值对左右区间的划分,递归左右区间。
1.为什么是从右边开始遍历,而不是从左边开始遍历?
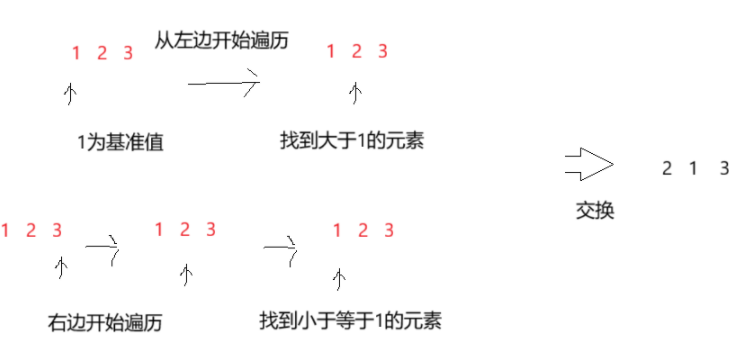
如果从左边开始遍历,会导致以基准值划分的区域不满足条件,如上图划分后左边区间存在大于基准值1的元素,不满足划分条件。
- 左边需要交换的元素为什么是大于基准值,而右边需要交换的元素是小于等于基准值?
左边的区域元素存放的元素小于等于基准值,当从左边开始遍历时,基准值的元素不会被替换,而是在终止条件满足(left >= right)后再进行交换;右边存放的元素是大于基准值的,小于等于基准值的元素应该位于左边区域。
//快速排序//1.Hoare法:选定一个基准值target,划分左右区间//先右遍历,找到不符合区间的值,后左遍历,找到不符合左边区间的值//交换,,最后交换基准值和left下标public void quickSort(int[] arr) {quickSort(arr,0,arr.length - 1);}private void quickSort(int[] arr,int left,int right){if(left >= right) return;//确保区间合法int target = arr[left];int l = left,r = right;while (left < right) {//找到右边不大于target的值while (left < right && arr[right] > target) right--;//找到左边不小于target的值while (left < right && arr[left] <= target) left++;//找到了交换int tem = arr[left];arr[left] = arr[right];arr[right] = tem;}//基准值位置与当前left下标位置交换arr[l] = arr[left];arr[left] = target;//划分左区间和右区间quickSort(arr,l,left - 1);quickSort(arr,left + 1,r);}
public static void main(String[] args) {Solution s = new Solution();int[] arr = {54,2,62,63,22,44,22,7,33};s.quickSort(arr);for(int x : arr) System.out.print(x + " ");}

4.2 挖坑法
快速排序的实现除了koare法外,还有外坑法,从右边开始遍历,发现小于等于基准值的元素就将该元素覆盖到当前left下标的位置,然后从左边遍历,找到大于基准值的元素就将该元素存放在当前下标为right的位置,一直重复该循环,当循环终止时,将基准值存放在left位置,完成区间划分,最后递归左右区间。
以数组【4,2,3,1】为例子

public void quickSort(int[] arr) {quickSort2(arr,0,arr.length - 1);}private void quickSort2(int[] arr,int left,int right){if(left >= right) return;int target = arr[left];int l = left,r = right;while (left < right) {//找到右边不大于target的值while (left < right && arr[right] > target) right--;arr[left] = arr[right];//找到左边不小于target的值while (left < right && arr[left] <= target) left++;arr[right] = arr[left];}//当前left位置存放基准值arr[left] = target;//划分左区间和右区间quickSort2(arr,l,left - 1);quickSort2(arr,left + 1,r);}
4.3 快慢双指针
快慢双指针法:定义两个终止slow和fast,以第一个元素为基准值,从左往右遍历数组,当发现当前快指针指向元素小于基准值并且慢指针 + 1 不等于快指针就进行元素的交换,最后交换基准值位置和慢指针位置的元素,完成左右区间划分后递归左右区间。
1.交换的条件为什么要满足慢指针 + 1 != 快指针?
因为如果快慢指针是相邻的,说明当前快指针在前的元素都是满足小于等于目标值的,不需要交换,例如:【33,22,12,11,55,43】。
在遍历到元素11时,11前面的元素都是小于等于target值33

元素遍历到55时,不满足交换条件,此时要让fast++,而慢指针slow不需要,最后遍历到43也不满足条件,fast++,结束遍历。

//快慢双指针:满足条件 arr[fast] <= target && arr[++slow] != arr[fast]交换public void quickSort3(int[] arr,int left,int right){if(left >= right) return;//1.定义快慢双指针int slow = left;int fast = slow + 1;//目标值int target = arr[left];//2.遍历数组while (fast <= right) {//交换:快指针指向元素小于等于目标值 并且 快慢双指针不相邻if(arr[fast] <= target && arr[++slow] != arr[fast]){int tem = arr[slow];arr[slow] = arr[fast];arr[fast]= tem;}fast++;}//将目标值存放在慢指针位置arr[left] = arr[slow];arr[slow] = target;//递归左右区间quickSort3(arr,left,slow - 1);quickSort3(arr,slow + 1,right);}
4.4 栈实现快速排序
//使用栈,保存划分的区间public void quickSortNonr(int[] arr){//创建一个栈Stack<Integer> stack = new Stack<Integer>();//开始的区间:0 - arr.length - 1stack.push(0);stack.push(arr.length - 1);while(!stack.empty()){//出栈int right = stack.pop();int left = stack.pop();//判断是否区间合法if(left >= right) continue;//调用方法:此处的partition方法是在快慢双指针方法的基础上最后慢指针的值int index = partition(arr,left,right);//将左右区间范围入栈:先加入右,后加入左stack.push(index + 1);stack.push(right);stack.push(left);stack.push(index - 1);}}//快慢双指针:满足条件 arr[fast] <= target && arr[++slow] != arr[fast]交换public int partition(int[] arr,int left,int right){//1.定义快慢双指针int slow = left;int fast = slow + 1;//目标值int target = arr[left];//2.遍历数组while (fast <= right) {//交换:快指针指向元素小于等于目标值 并且 快慢双指针不相邻if(arr[fast] <= target && arr[++slow] != arr[fast]){int tem = arr[slow];arr[slow] = arr[fast];arr[fast]= tem;}fast++;}//将目标值存放在慢指针位置arr[left] = arr[slow];arr[slow] = target;return slow;}4.5 时间消耗
public static void main(String[] args) {Solution s = new Solution();int[] arr = new int[10000];for(int i = 0;i < 10000;i++) arr[i] = 10000 - i;int[] arr1 = Arrays.copyOf(arr,arr.length);int[] arr2 = Arrays.copyOf(arr,arr.length);long s1 = System.currentTimeMillis();s.insertSort(arr);long e1 = System.currentTimeMillis();System.out.println("直接插入排序需要的时间:" + (e1 - s1));long s2 = System.currentTimeMillis();s.shellSort1_1(arr1);long e2 = System.currentTimeMillis();System.out.println("希尔排序的时间:" + (e2 - s2));long s3 = System.currentTimeMillis();s.quickSort(arr2);long e3 = System.currentTimeMillis();System.out.println("快速排序的时间:" + (e3 - s3));}
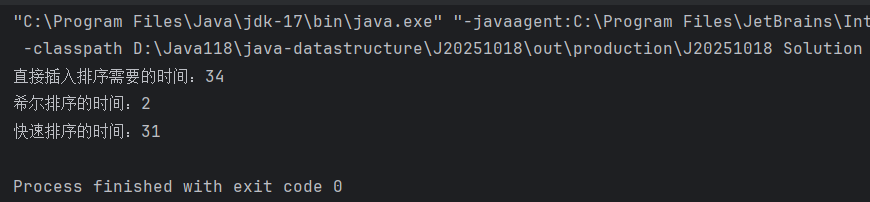
4.6 快速排序的优化
快速排序的优化:三数取中法
去数组的最左边元素和最右边元素和中间元素三者比较,取中间值作为基准值,交换的次数可以得到优化,数组【5,1,2,3,4】,如果选定5作为基准值,就需要将1,2,3,4元素交换到5前面,而选定中间值2,只需要将5元素交换到4后面即可,减少了交换的次数。
private int three_num_mid(int[] arr,int left,int right,int mid){//比较三个数的大小,返回中间索引if(arr[left] > arr[right]){if(arr[mid] > arr[left]) return left;else if(arr[right] > arr[mid]) return right;else return mid;}else{if(arr[mid] > arr[right]) return right;else if(arr[left] > arr[mid]) return left;else return mid;}}private void quickSort(int[] arr,int left,int right){if(left >= right) return;int l = left,r = right;int mid = l + (r - l) / 2;int indext = three_num_mid(arr,l,r,mid)int target = arr[index];//原来排序的基础上更改目标值//将目标值位于首位arr[index] = arr[l];arr[l] = target;while (left < right) {//找到右边不大于target的值while (left < right && arr[right] > target) right--;//找到左边不小于target的值while (left < right && arr[left] <= target) left++;//找到了交换int tem = arr[left];arr[left] = arr[right];arr[right] = tem;}//基准值位置与当前left下标位置交换arr[l] = arr[left];arr[left] = target;//划分左区间和右区间quickSort1(arr,l,left - 1);quickSort1(arr,left + 1,r);
}
快速排序时间复杂度:O(NlogN) - O(N^2)第一次区间是0 - length ,遍历一遍数组,遍历元素为N,
第二划分左区间【left,index - 1] 与 右区间【index + 1,right】 遍历的元素也是N,
-------
第logN 次划分,2^(logN)个区间,遍历元素也是N总的遍历次数是N * logN,划分的层数是二叉树的高度,如果极端情况下划分的区间是单个区间的,
在二叉树上是退化为单分支,时间复杂度就是O(N^2);空间复杂度:O(logN) - O(N)递归过程划分的区间的个数可以看作二叉树节点数,递归过程深度越深,栈区占用
空间就越多,因此递归的空间复杂度可以间接的用递归深度表示,而递归的深度与
二叉树类似,高度为logN,最坏情况下退化为单分支,高度为N。
5.归并排序
归并排序的思想是间待排序的区间不断的划分一个个更小的区间,划分的终止条件为区间元素个数小于等于0,区间划分好后进行排序,排序完成将一个个小的区间合并,完成排序。
例子:给定一个数组【3,4,1,77,33,11,97,68】,使用归并排序完成排序。
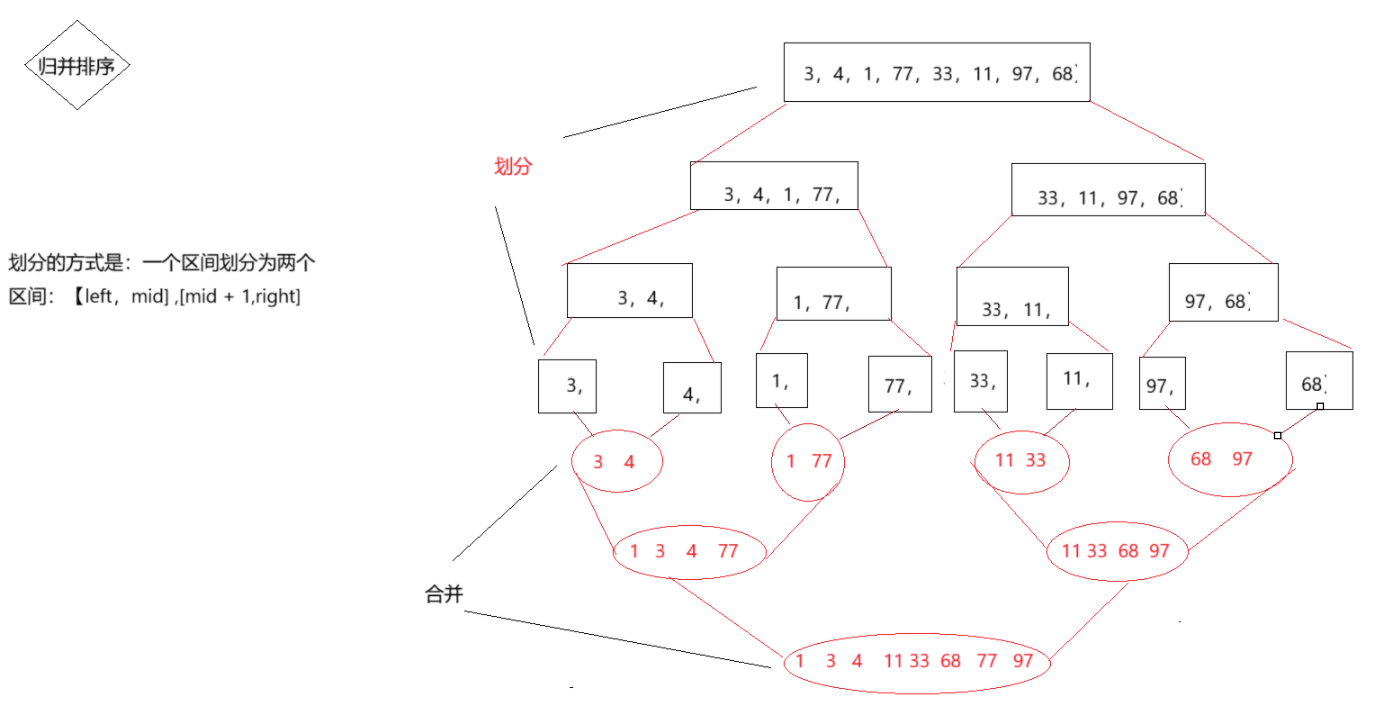
//归并排序public void mergerSort(int[] arr){mergerSort(arr,0,arr.length - 1);}public void mergerSort(int[] arr,int left,int right){if(right - left < 1) return;//划分左右区间int mid = left + (right - left) / 2;//递归划分左右区间mergerSort(arr,left,mid);mergerSort(arr,mid+1,right);/*** 可以在此处先排序划分的左右区间* 也可以在merger函数中在排序合并*///合并数组merger(arr,left,mid,right);}private void merger(int[] arr,int left,int mid,int right){//创建一个临时数组,大小为划分区间的长度int[] tem = new int[right - left + 1];int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;//合并数组int k = 0;//临时数组索引while(s1 <= e1 && s2 <= e2){if(arr[s1] <= arr[s2] ) tem[k++] = arr[s1++];else tem[k++] = arr[s2++];}//判断是否左区间还剩元素while(s1 <= e1) tem[k++] = arr[s1++];//判断是否右区间还剩元素while(s2 <= e2) tem[k++] = arr[s2++];//将临时数组拷贝到原数组for (int i = 0;i < tem.length;i++){arr[left++] = tem[i];}}

非递归实现归并排序,调用合并的方法,第一层循环判断分组的大小,第二层循环进行排序。
public void mergerSortNonR(int[] arr){int gap = 1;//确保一个组中元素个数小于数组长度while(gap < arr.length){//gap = 1 时 一个组一个元素,将两个元素和并//gap = 2 -> 4个元素//----for (int i = 0; i < arr.length; i += 2*gap) {int left = i;//防止越界int mid = left + gap - 1;if(mid >= arr.length) mid = arr.length - 1;//防止越界int right = mid + gap;if(right >= arr.length) right = arr.length - 1;//合并merger(arr,left,mid,right);}//扩大组中元素个数gap *= 2;}}private void merger(int[] arr,int left,int mid,int right){//创建一个临时数组,大小为划分区间的长度int[] tem = new int[right - left + 1];int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;//合并数组int k = 0;//临时数组索引while(s1 <= e1 && s2 <= e2){if(arr[s1] <= arr[s2] ) tem[k++] = arr[s1++];else tem[k++] = arr[s2++];}//判断是否左区间还剩元素while(s1 <= e1) tem[k++] = arr[s1++];//判断是否右区间还剩元素while(s2 <= e2) tem[k++] = arr[s2++];//将临时数组拷贝到原数组for (int i = 0;i < tem.length;i++){arr[left++] = tem[i];}}
合并排序时间复杂度:O(N*logN)
合并中每一层的元素都是N,一共有logN层,合并中遍历的元素个数N * logN空间复杂度:O(N * logN) 归并排序的空间复杂度并不是通过累加递归过程中的空间来计算的。重要的一点是,尽管每次合并
操作都需要申请额外的内存空间,但在合并完成之后,这些临时开辟的内存空间就被释放掉了。
任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大
也不会超过 n 个数据的大小,因此归并排序的空间复杂度是 O(n)。对比上面几种排序消耗的时间
public static void main(String[] args) {Solution s = new Solution();int[] arr = new int[10000];for(int i = 0;i < 10000;i++) arr[i] = 10000 - i;int[] arr1 = Arrays.copyOf(arr,arr.length);int[] arr2 = Arrays.copyOf(arr,arr.length);int[] arr3 = Arrays.copyOf(arr,arr.length);int[] arr4 = Arrays.copyOf(arr,arr.length);int[] arr5 = Arrays.copyOf(arr,arr.length);long s1 = System.currentTimeMillis();s.insertSort(arr);long e1 = System.currentTimeMillis();System.out.println("直接插入排序需要的时间:" + (e1 - s1));long s2 = System.currentTimeMillis();s.shellSort1(arr1);long e2 = System.currentTimeMillis();System.out.println("希尔排序的时间:" + (e2 - s2));long s3 = System.currentTimeMillis();s.quickSort(arr2);long e3 = System.currentTimeMillis();System.out.println("快速排序的时间:" + (e3 - s3));long s4 = System.currentTimeMillis();s.mergerSort(arr3);long e4 = System.currentTimeMillis();System.out.println("归并排序的时间:" + (e4 - s4));long s5 = System.currentTimeMillis();s.selectSort(arr4);long e5 = System.currentTimeMillis();System.out.println("选择排序的时间:" + (e5 - s5));long s6 = System.currentTimeMillis();Arrays.sort(arr5);long e6 = System.currentTimeMillis();System.out.println("idea系统排序的时间:" + (e6 - s6));}
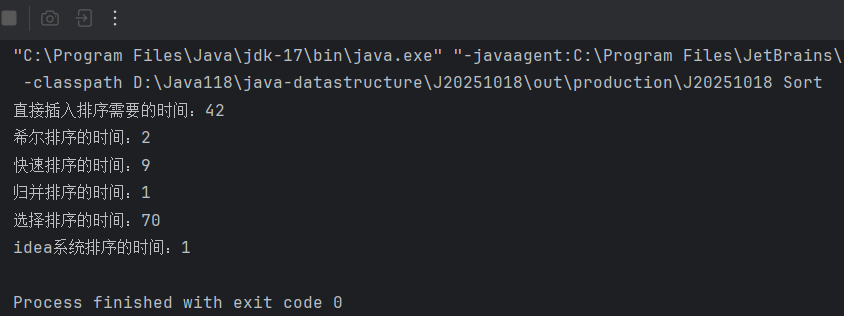
6.常见排序的时空复杂度