17.AVL树的实现(一)

一.AVL树的概念

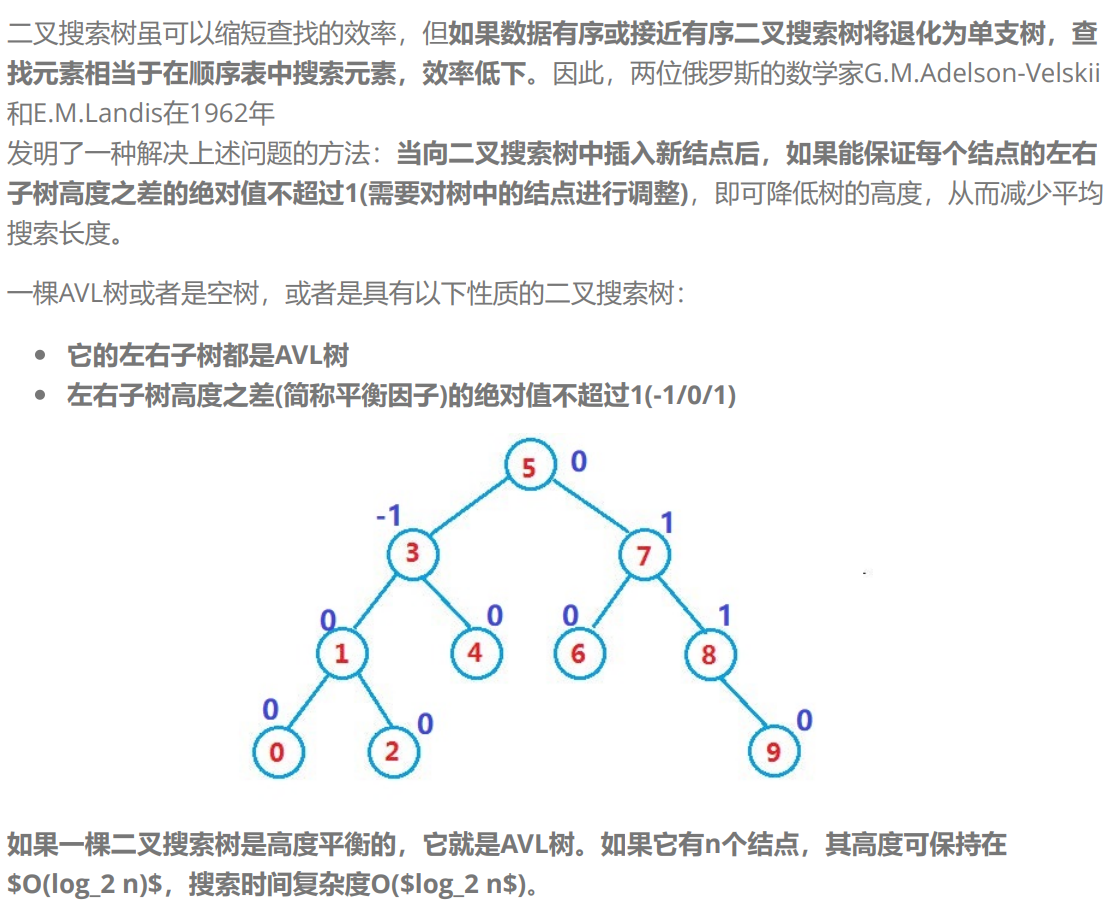
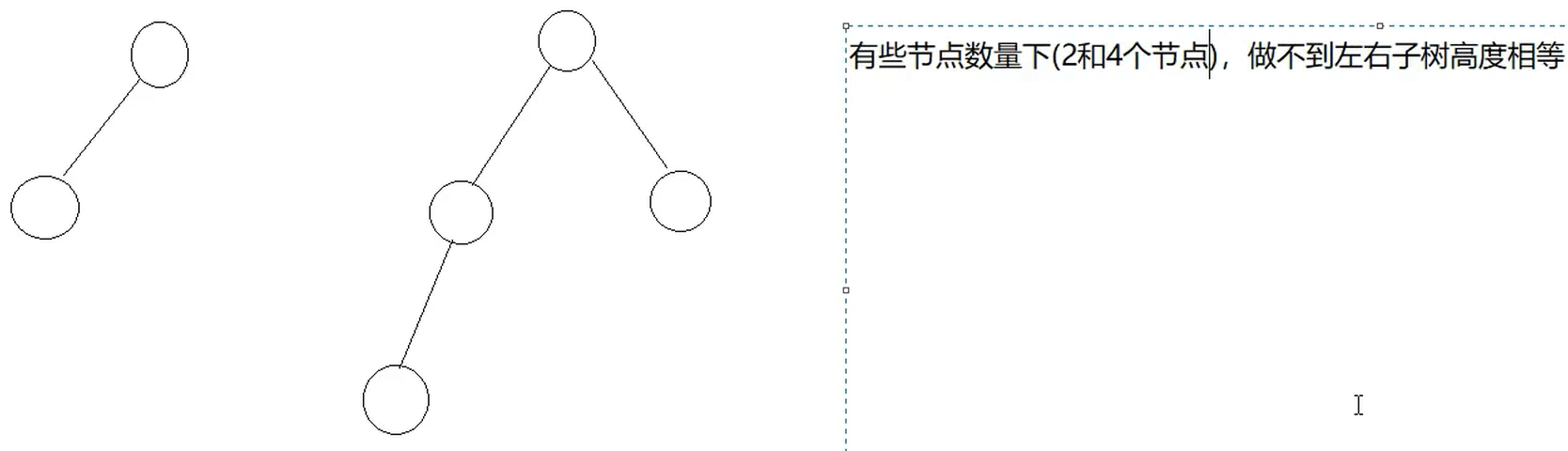
只有满二叉树才能做的高度差一致

二.平衡因子的更新探讨

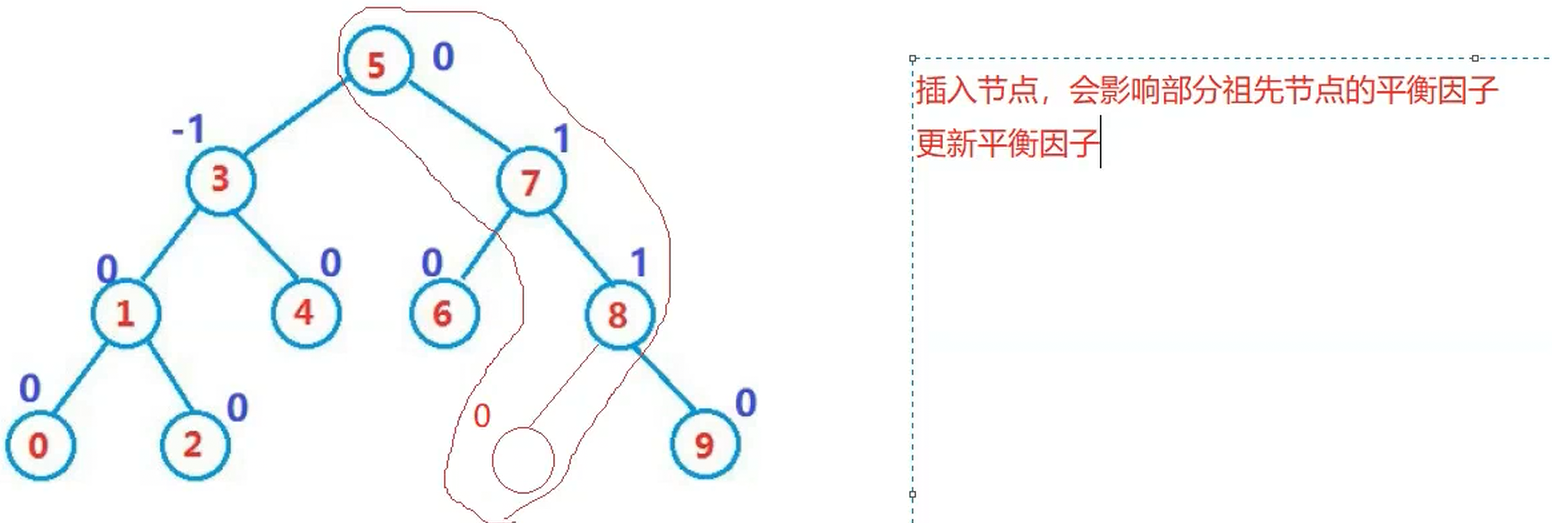
那我们的平衡因子怎么进行更新呢?

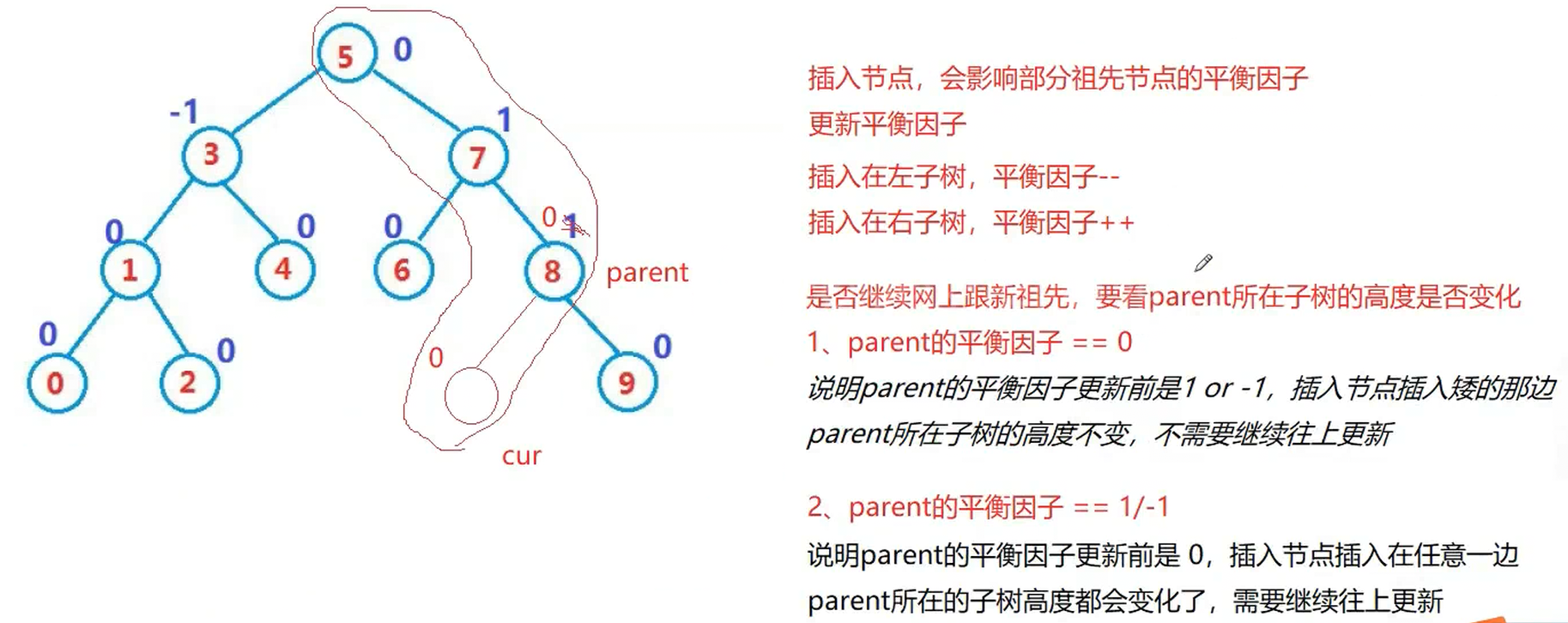
三.AVL树的基本定义实现

1.AVL树节点设计

template<class K,class V>
struct AVLTreeNode
{pair<K,V> _kv;AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;int _bf;AVLTreeNode(const pair<K,V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};

我们在这里每一个树上的节点,都进行了增加我们的_bf(平衡因子) 和 _parent(父亲节点),等会就在我们的操作上要加上对这个元素的修改

2.AVL树的大体设计

template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K,V> Node;
public:Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}~AVLTree(){Destroy(_root);_root = nullptr;}AVLTree() = default;AVLTree(const AVLTree<K,V>& t){_root = Copy(t._root);}AVLTree<K,V>& operator=(AVLTree<K,V> t){swap(_root,t._root);return *this;}private:Node* Copy(Node* root){if(root == nullptr){return nullptr;}Node* newRoot = new Node({root->_key,root->_value});newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}//销毁这里,我们要使用后续递归void Destroy(Node* root){if(root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}private:Node* _root = nullptr;
};

3.insert()的实现

insert的实现,需要我们进行更新平衡因子

 bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while(parent){if(cur == parent->_left){parent->_bf --;}else{parent->_bf ++;}if(parent->_bf == 0){break;}else if(parent->_bf == -1 || parent->_bf == 1){//继续往上更新cur = parent;parent = parent->_parent;}else if(parent->_bf == -2 || parent->_bf == 2){//不平衡了,旋转处理}else{assert(false);}}return true;}

这里我们对于_bf = 2 和 -2的场景还没有继续实现,先来总结一下我们前面写的:

四.AVL树的旋转

1.新节点插入较高左子树的左侧---左左：右单旋

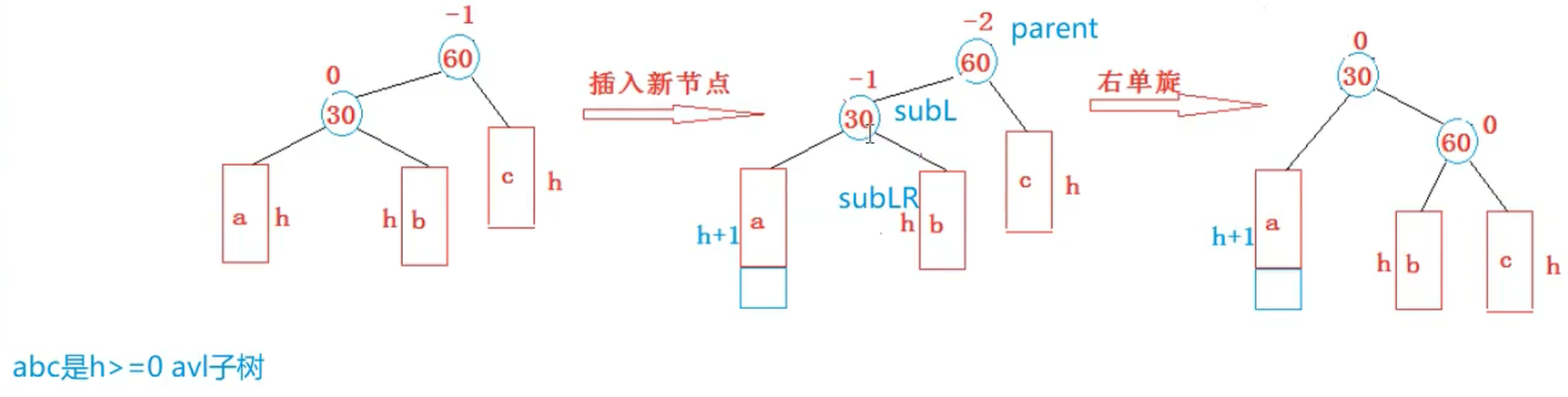
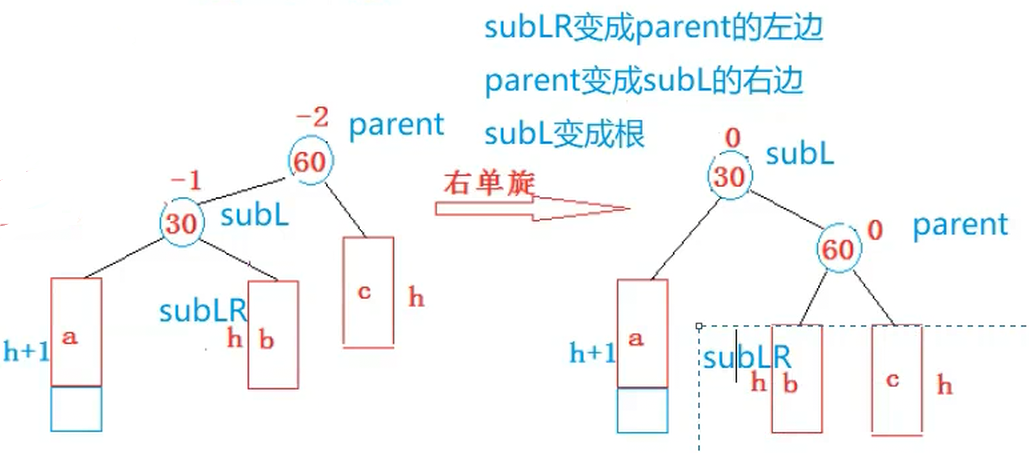
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if(subLR != nullptr){subLR->_parent = parent;}Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if(parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if(parent == parentParent->_right){parentParent->_right = subL;}else{parentParent->_left = subL;}subL->_parent = parentParent;}parent->_bf = subL->_bf = 0;}

2.新节点插入较高右子树的右侧---右右：左单旋

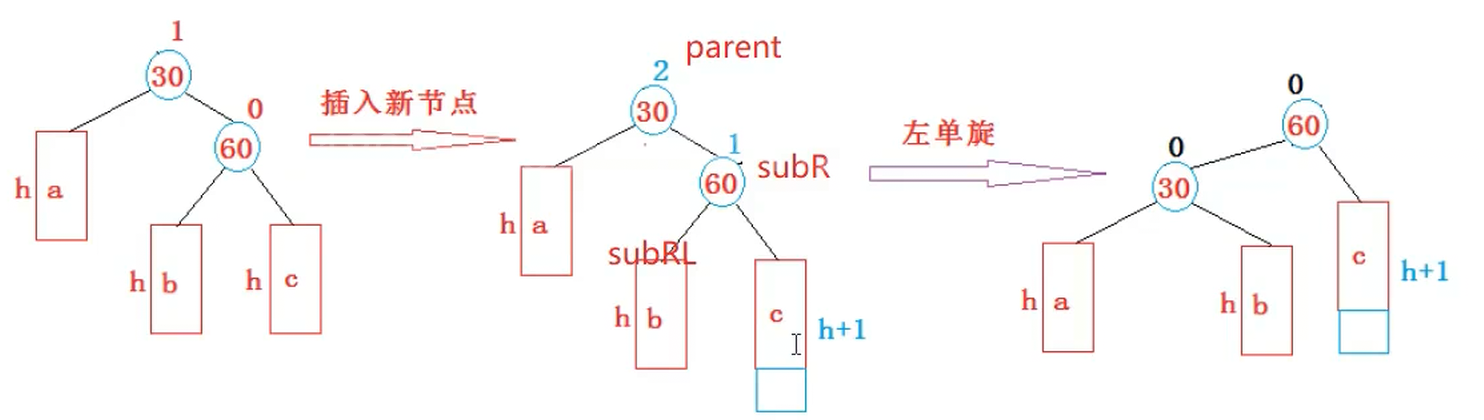
我们上面使用的就是抽象图,如果不使用抽象图,那么我们的搜索树的种类就太多了

如:h = 3的AVL子树,往上面要进行翻转的情况一共有6120种(可以自己尝试推导一下,这里我们不进行讲解,如下图(不了解也可以))

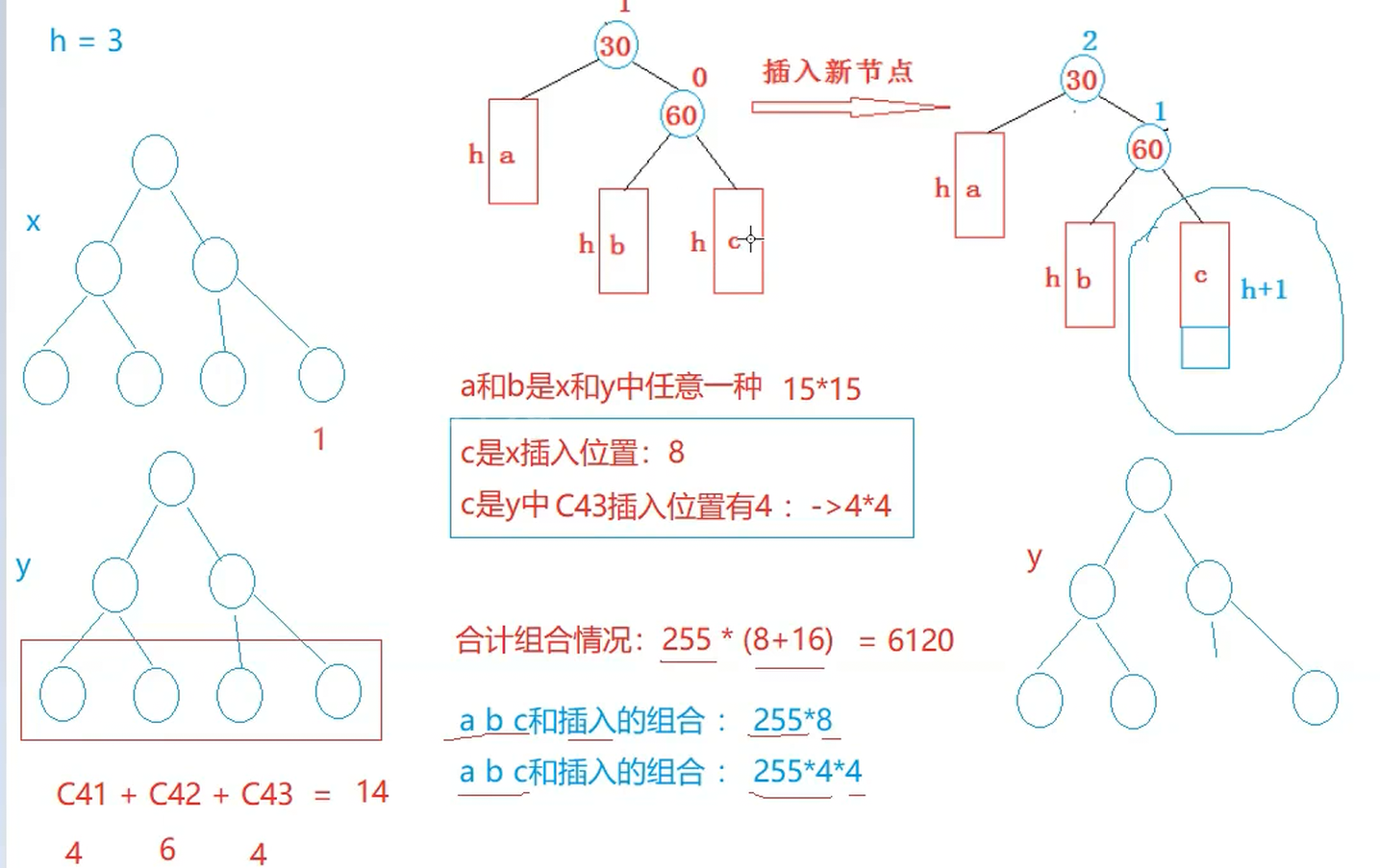
我们在进行旋转的时候,根本就不关系我们的下面的点究竟是怎么样的

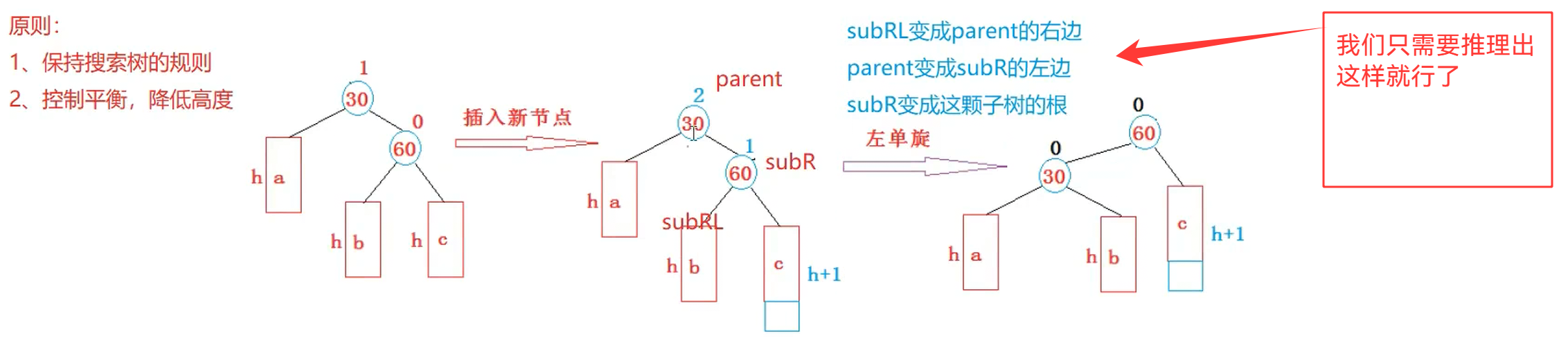
我们可以尝试看一看这个地方,我们的逻辑是否是正确的?(当然是不对的)

每一个树节点的_parent的要进行修改,并且还要进行修改我们的_bf(你使用了他,那么你就要进行维护他)

_parent好修改,那么我们的_bf怎么进行修改呢?

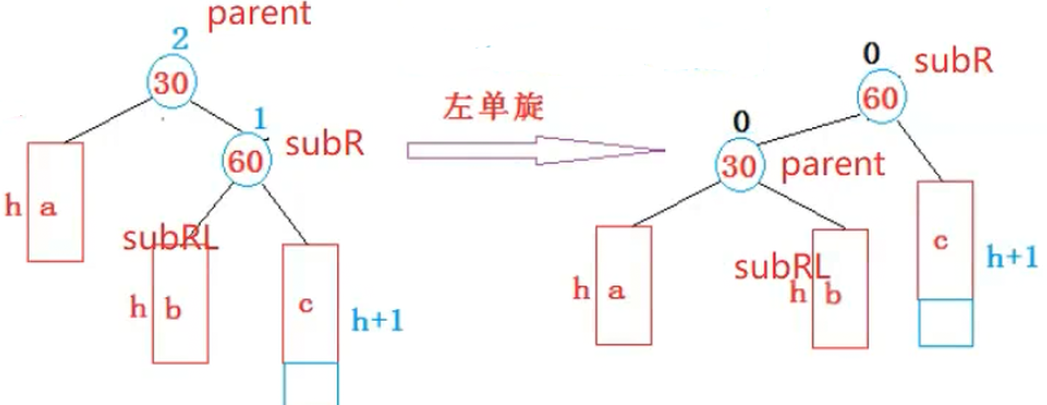
我们可以看到,a,b,c的孩子都没有动过,所以我们不需要修改他们,我们只需要修改parent和subR就行了

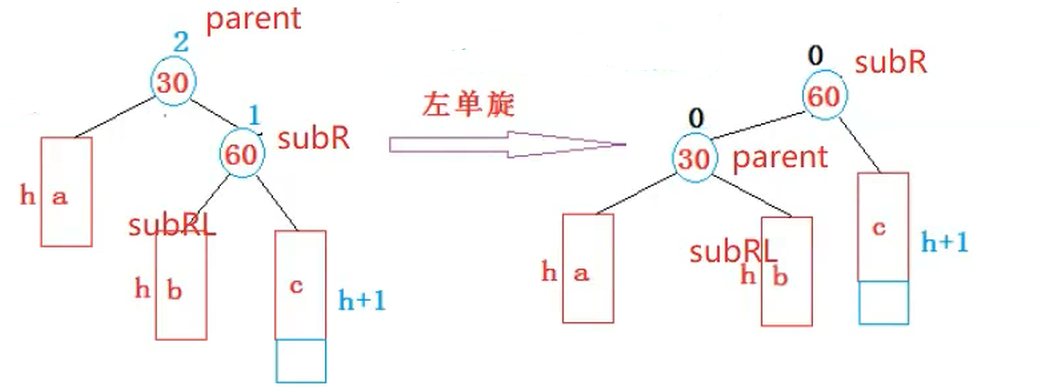
代码实现void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL != nullptr){subRL->_parent = parent;}Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if(parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if(parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;}

3. 新节点插入较高右子树的左侧---右左：先右单旋再左单旋

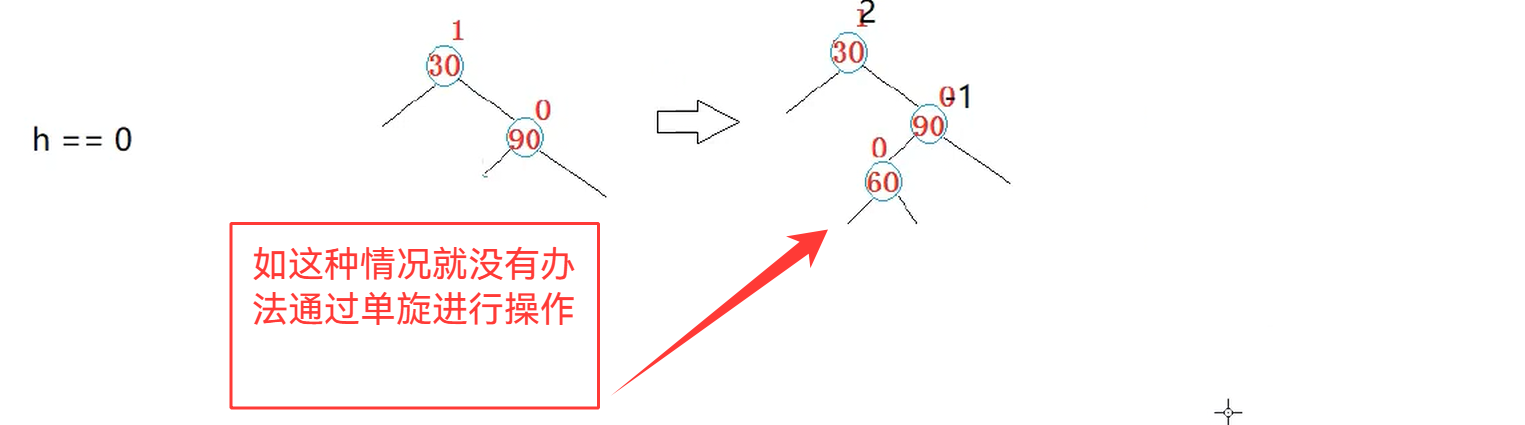
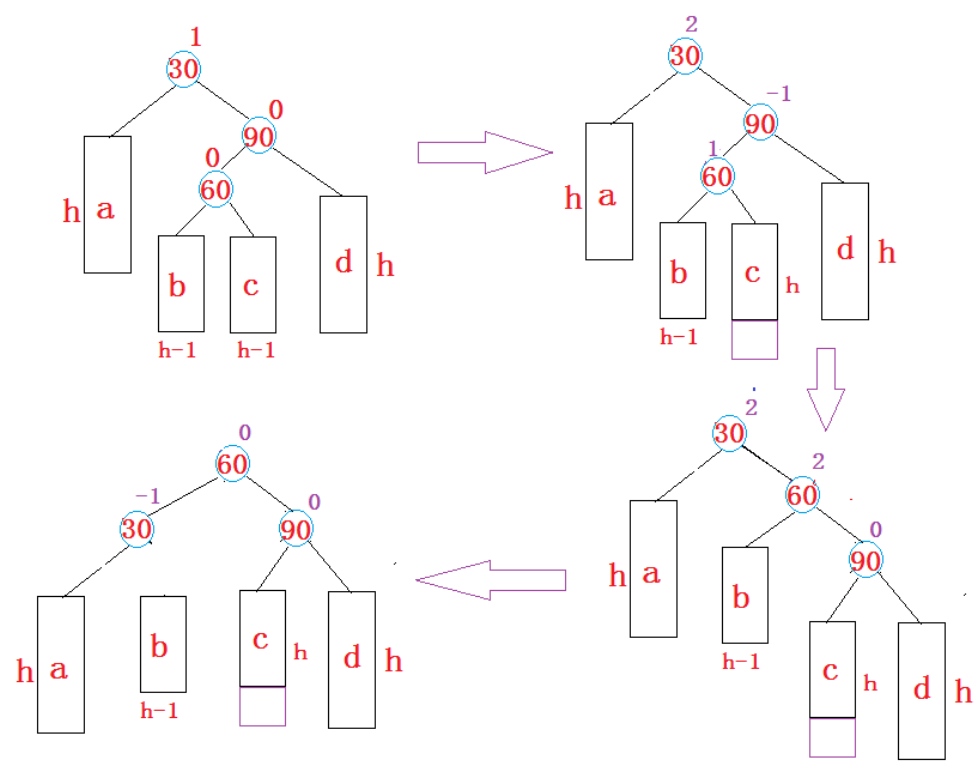
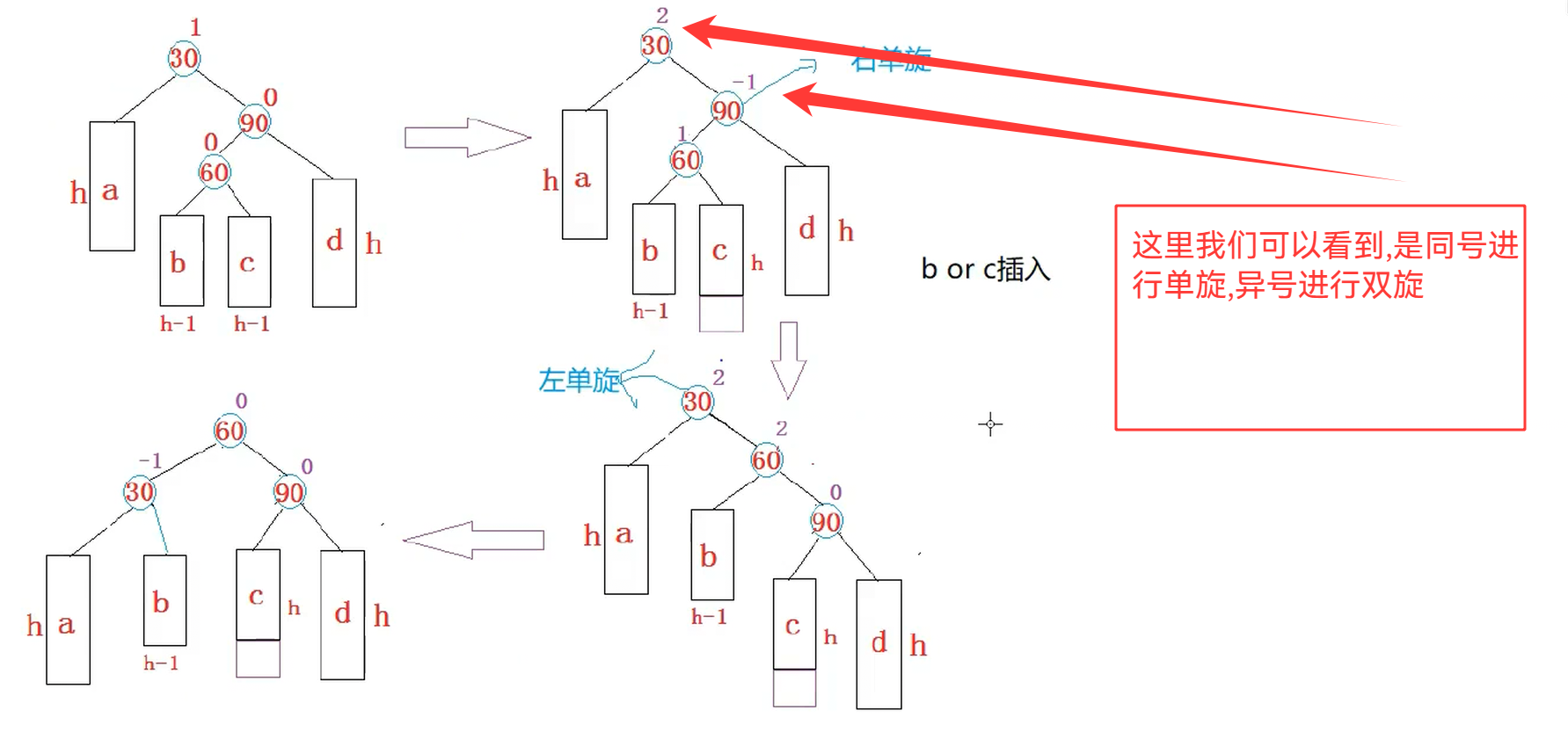
在这里就相当于是将我们的(60)变成根,然后(60)的孩子两边都分一个

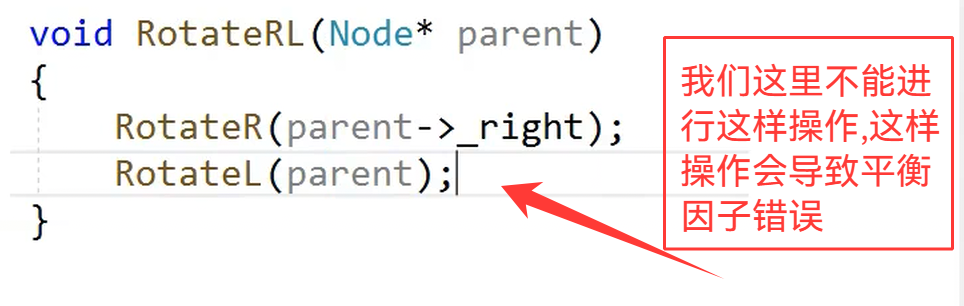
这个地方,我们可能有三种插入方式

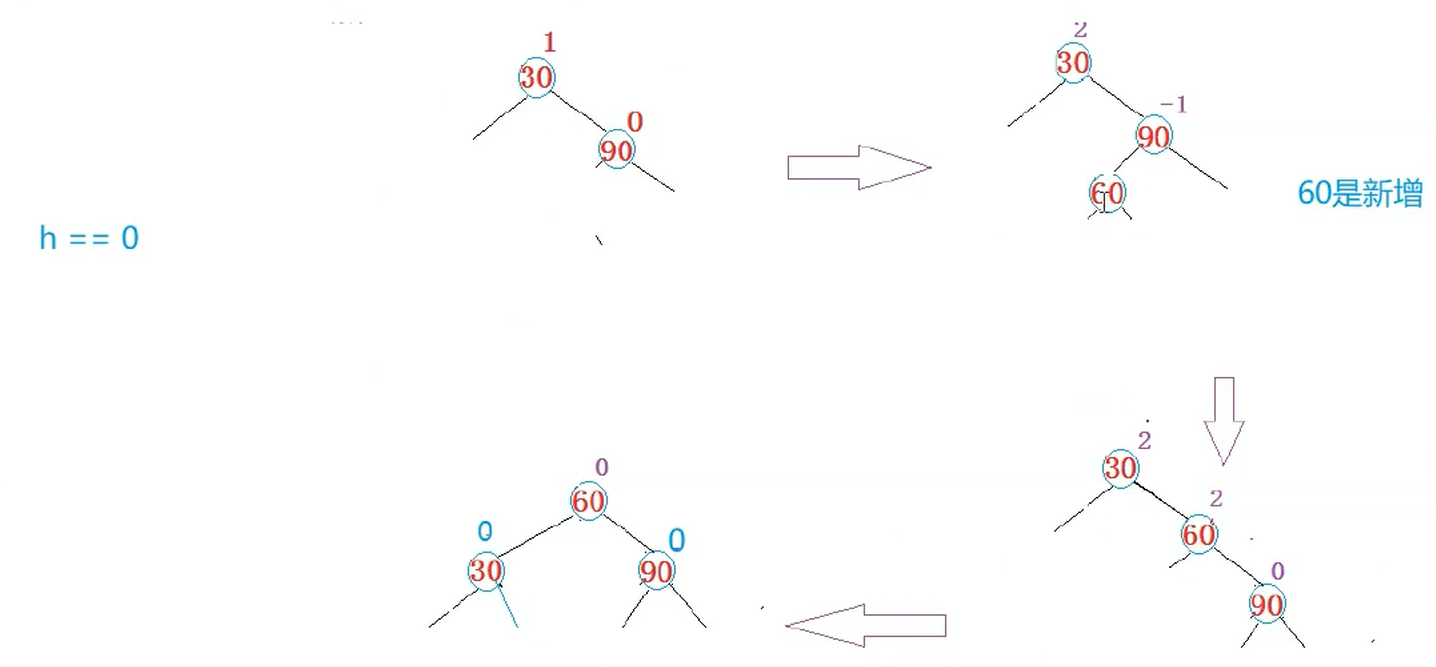
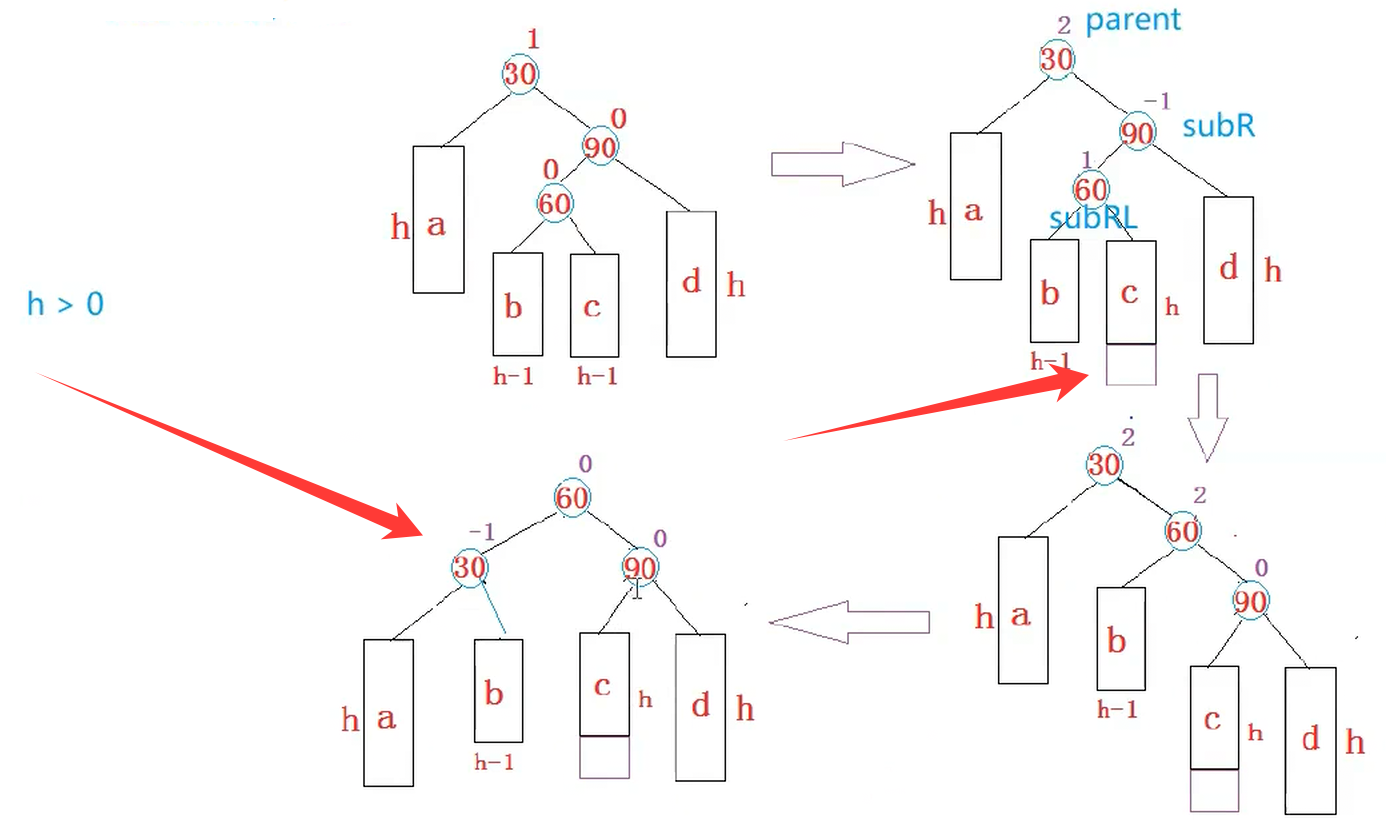
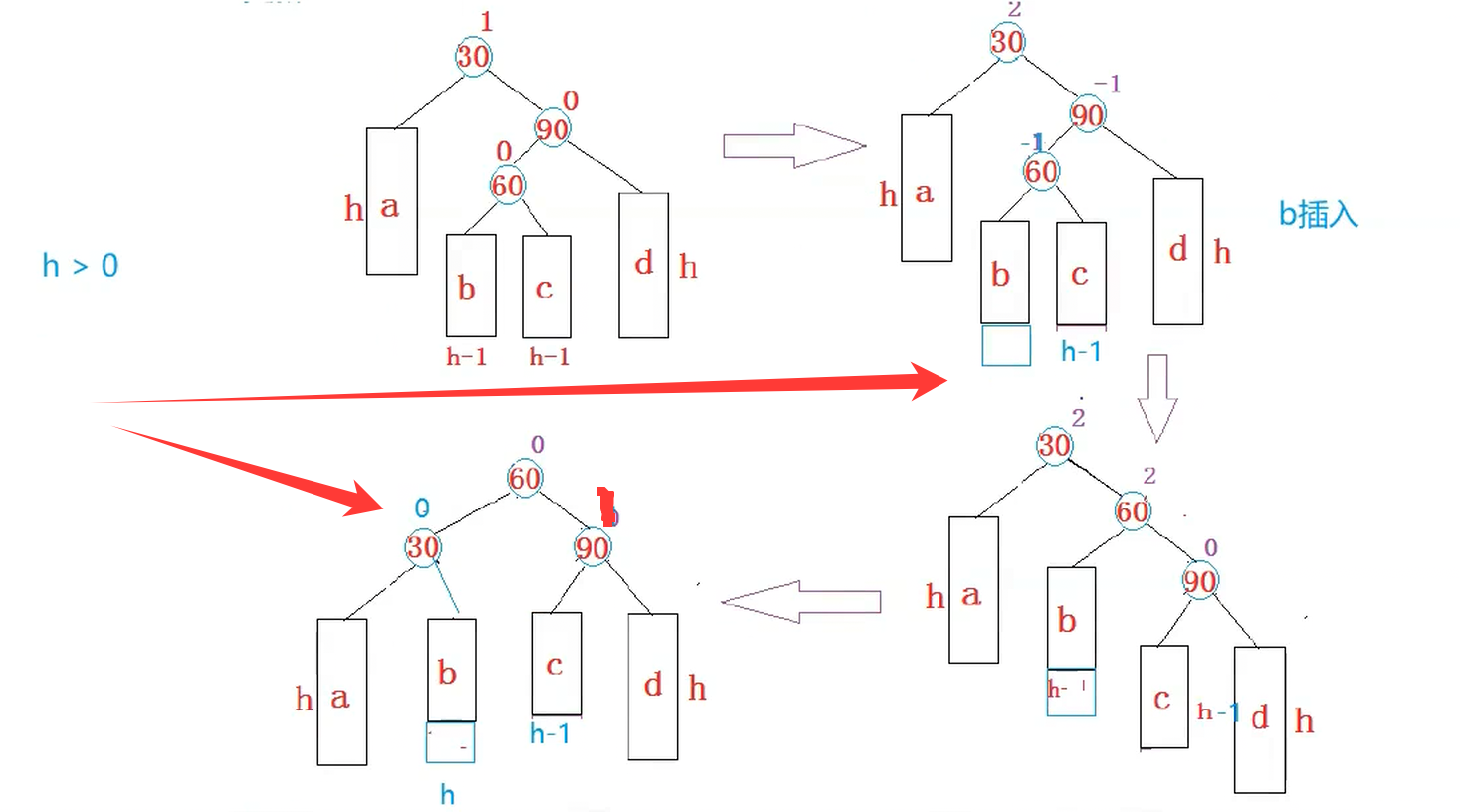
所以我们在旋转之后,处理我们的平衡因子即可

void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if(bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if(bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if(bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}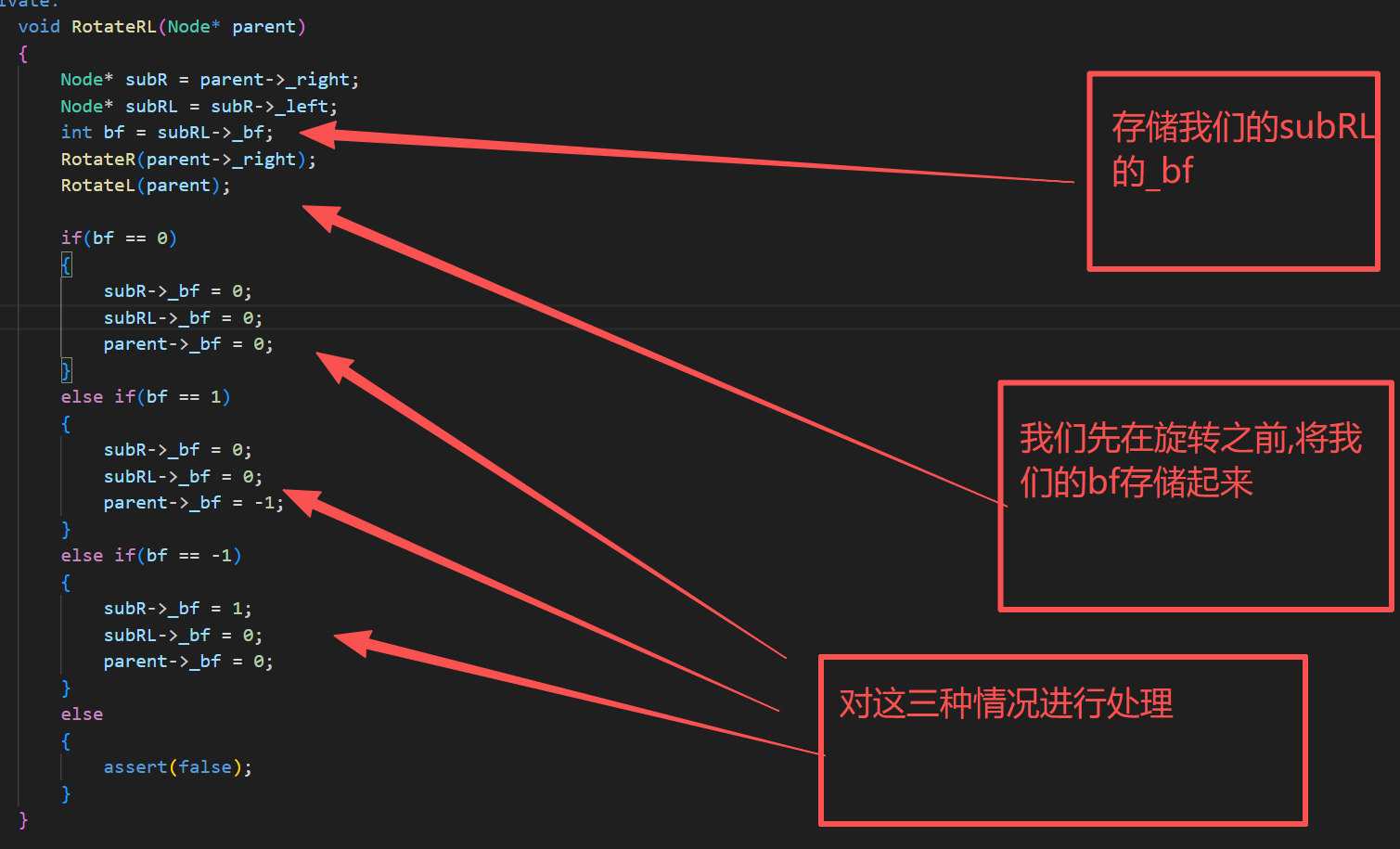

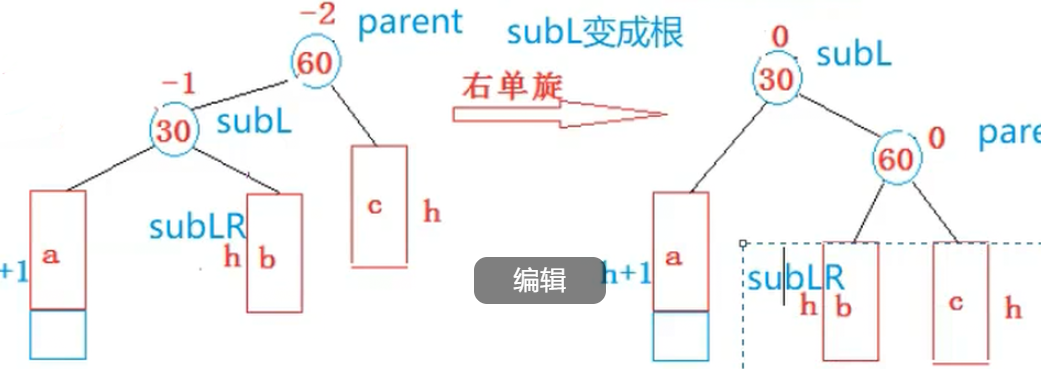
4.新节点插入较高左子树的右侧---左右：先左单旋再右单旋

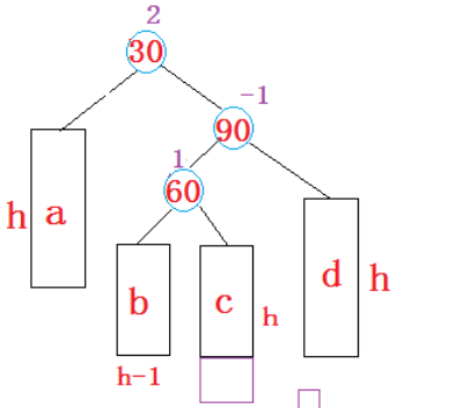
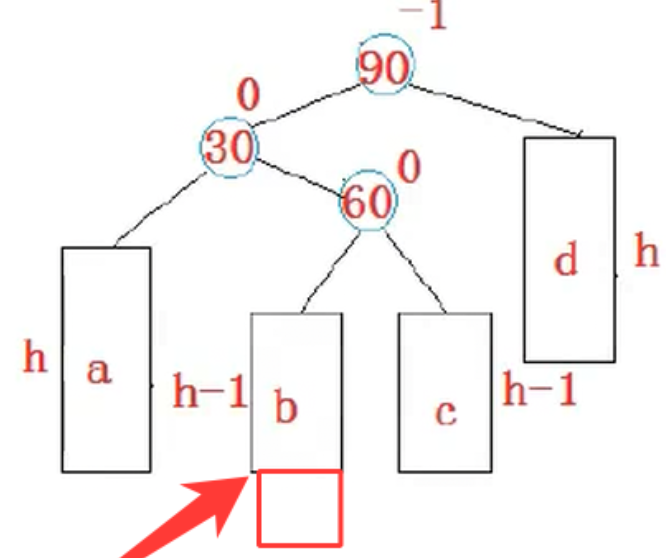
我们会发现有一种情况是单旋转没法解决的,如下:

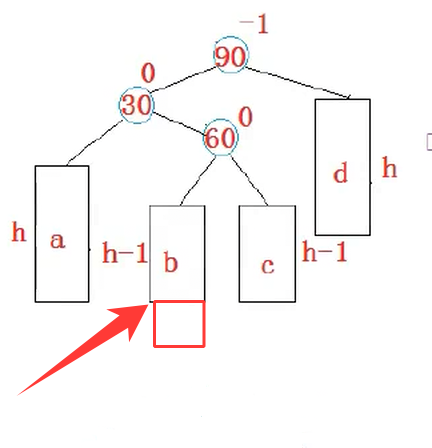
在我们该地方进行插入,那么单旋就没办法进行解决

和上面是一样的解决方式

void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}}

五.insert的实现

bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while(parent){if(cur == parent->_left){parent->_bf --;}else{parent->_bf ++;}if(parent->_bf == 0){break;}else if(parent->_bf == -1 || parent->_bf == 1){//继续往上更新cur = parent;parent = parent->_parent;}else if(parent->_bf == -2 || parent->_bf == 2){//不平衡了,旋转处理if(parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if(parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if(parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if(parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;}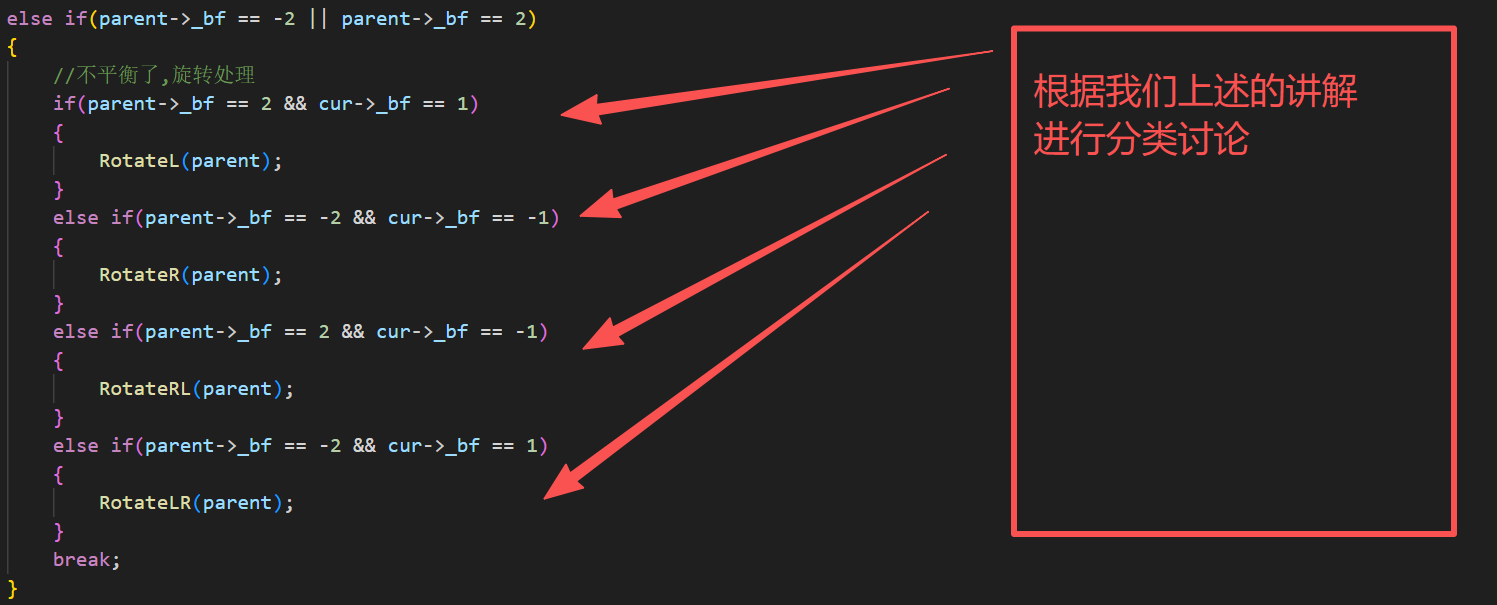

AVL代码后续补充