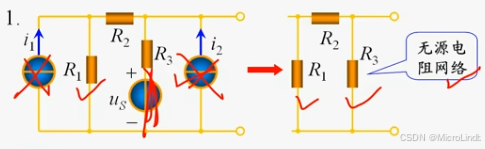
【电路·3】化简电路、等效变换、求输入电阻;其实很简单~
一、等效变换
1.一些基本的等效变换规则(极为重要)
1.理想电压源 和 电阻 并联
-> 电阻可以去掉
2.理想电流源 和 电阻 串联
-> 电阻可以去掉
3.理想电压源 和 电阻 串联
-> 可以变成 理想电流源 和 电阻 并联
4.理想电流源 和 电阻 并联
-> 可以变成 理想电压源 和 电阻 串联
2.例题1
化简此二端网络:
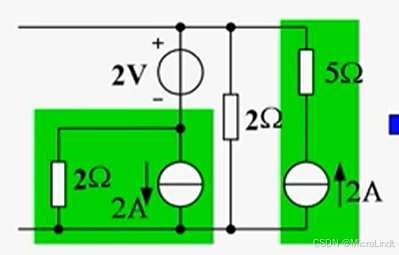
思路是这样的。
首先,和 电流源 串联 的所有电阻 都可以被去掉。(右侧)
我们还能够把 电流源 和 电阻的并联结构 转化成 -> 电压源 和 电阻 的串联结构。
因为,U = IR,所以转化后的电压源 U = 2A * 2Ω = 4V
因此可以变成下面这样:
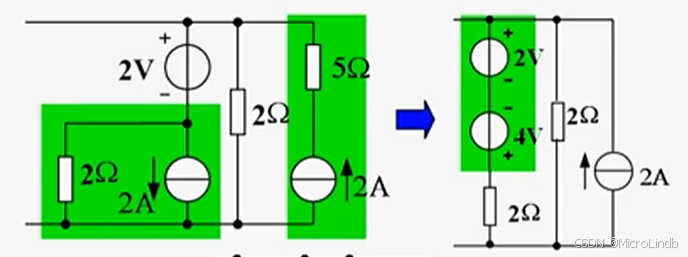
然后,我们将 2个 反向的理想电压源做代数和运算。
其中绝对值小的被抵消掉了。
所以变成这样:
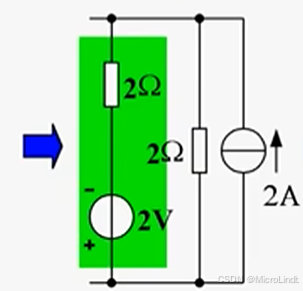
又因为,理想电压源 串联一个电阻的结构 能转化为 理想电流源 并联一个电阻的结构,
所以,可以变成这样:
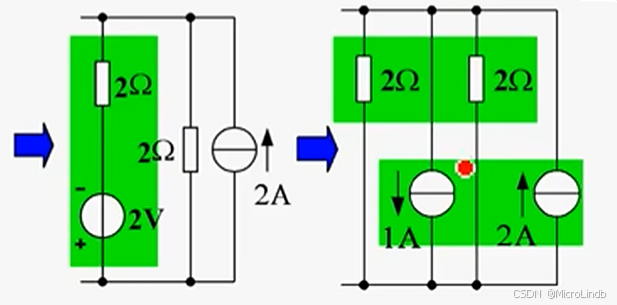
又因为,并联的电流源 可以抵消(就像 串联的电压源 那样,可以做代数和运算)
且,并联的 2个电阻 也可以化简成 1个电阻,
所以可以这样变化:
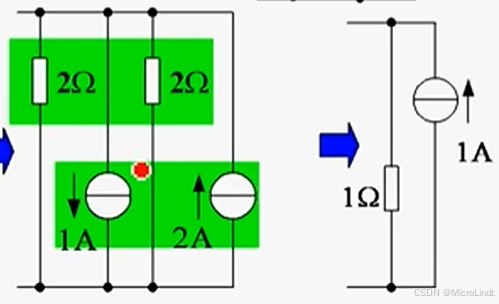
3.例题2
在这个里面,要先把上面的电阻移到下面来,利用等电位
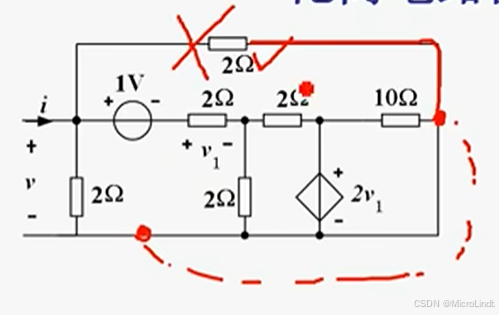
这样变换 ->
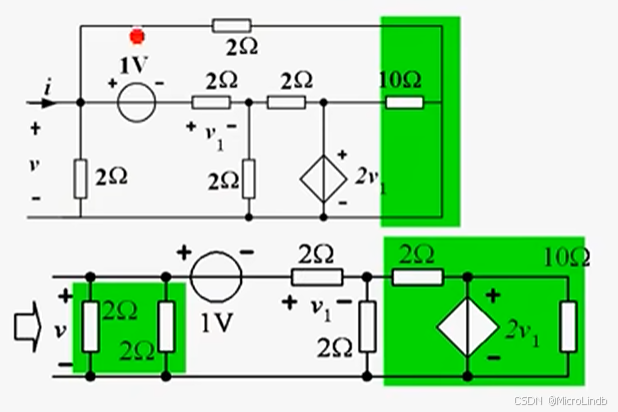
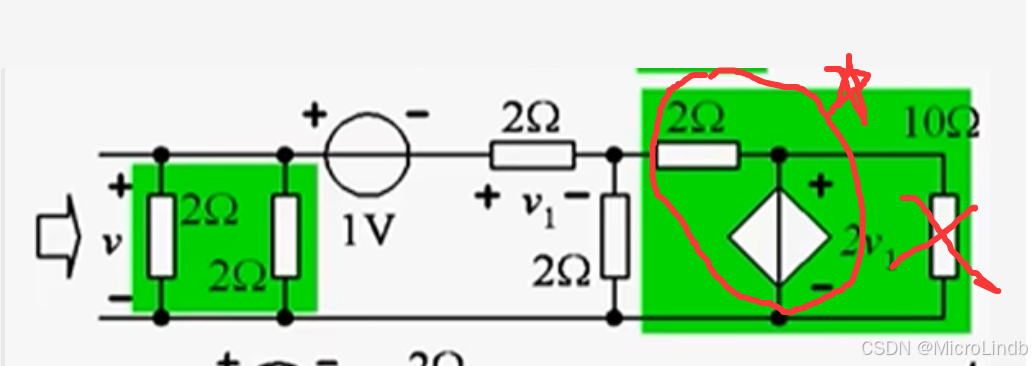
上图右边的 10Ω,去掉,然后可以看到圈住的位置有一个电压源和电阻串联,所以可以转化为一个电流源和电阻并联,因此,可以转化为下图:
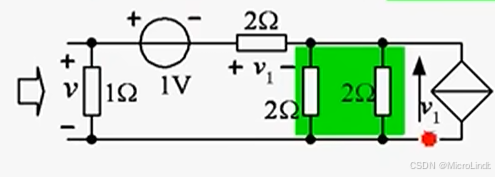
然后,我们将 2个并联的 2Ω 电阻合并为 1个并联了的 1Ω 电阻,
合并之后,又因为电流源和电阻并联可以转化为电压源和电阻串联,
所以最终化简为这样:
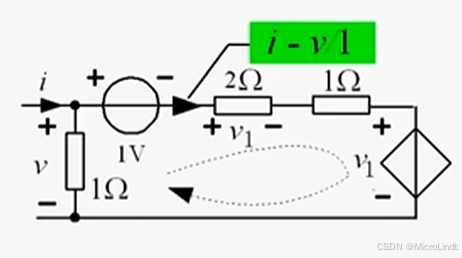
但这还不算结束。
二、公式法化简
1.根据函数关系直接列方程求解
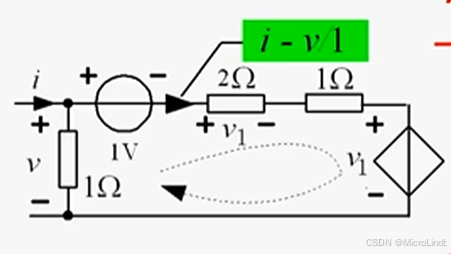
还是这个图,我们现在已知流入的电流是 i,整个电路里面的电压等势点电压都是 v。
所以,在右侧支路里面的电流电压关系可以用公式代替:
设右侧支路电流为 Is
Is = i - 左侧支路电流
Is = i - v/1
所以, 利用 KVL
v = 1 + v1 + v1/2 + v1
又因为 v1 = (i-v/1) * 2
所以代入得到:
v = 1 + 2(i-v) + 2(i-v)/2 + 2*(i-v)
v = 1 + 5i - 5v
6v = 1 + 5i
v = 1/6 + 5i/6
所以,知道了这个二端网络的 v 和 i 的关系之后,可以用以下的电路做等效替代:
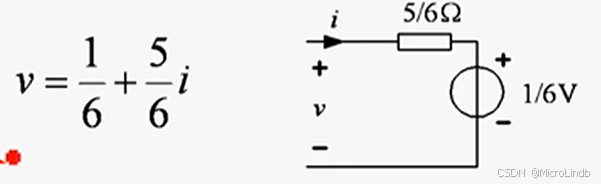
但这里有个疑惑,i = u/r = (5/6v) / (5/6Ω) = 1*i。
这默许了 r 的默认单位就是 1Ω…
不知道,明白了原理就好,细节不管了。
二、更多变换
1.输入电阻
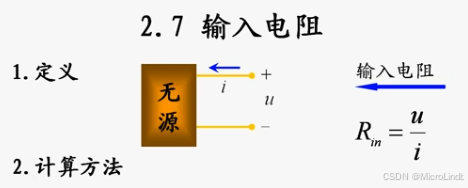
输入电阻,通俗来讲,
就是一堆串联并联混联的电阻集群。
比如说:
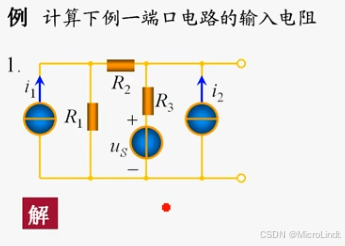
在计算输入电阻的时候,需要分析这个端口网络的性质:
分为 有源 和 无源
上面的例子就是一个有源端口网络。
如果遇到有源端口网络,那么,
电流源 可以看作一个 开路(断开,断路),
电压源 可以看作一个 短路(一根导线)
因此,一个有源网络,在求解 “输入电阻” 的时候,
其实可以变换为一个无源网络
所以上面的电路可以被等效变换为: