网站建设与维护薪资网页版梦幻西游答题器

今天给大家带来的是有关单调栈以及单调队列的有关知识，关于单调栈和单调队列的知识可以处理算法比赛中的小题，可以加快处理的时间复杂度。（注意对于这类题目的数组内的元素值都是固定的，并不能改变）

1.基本内容

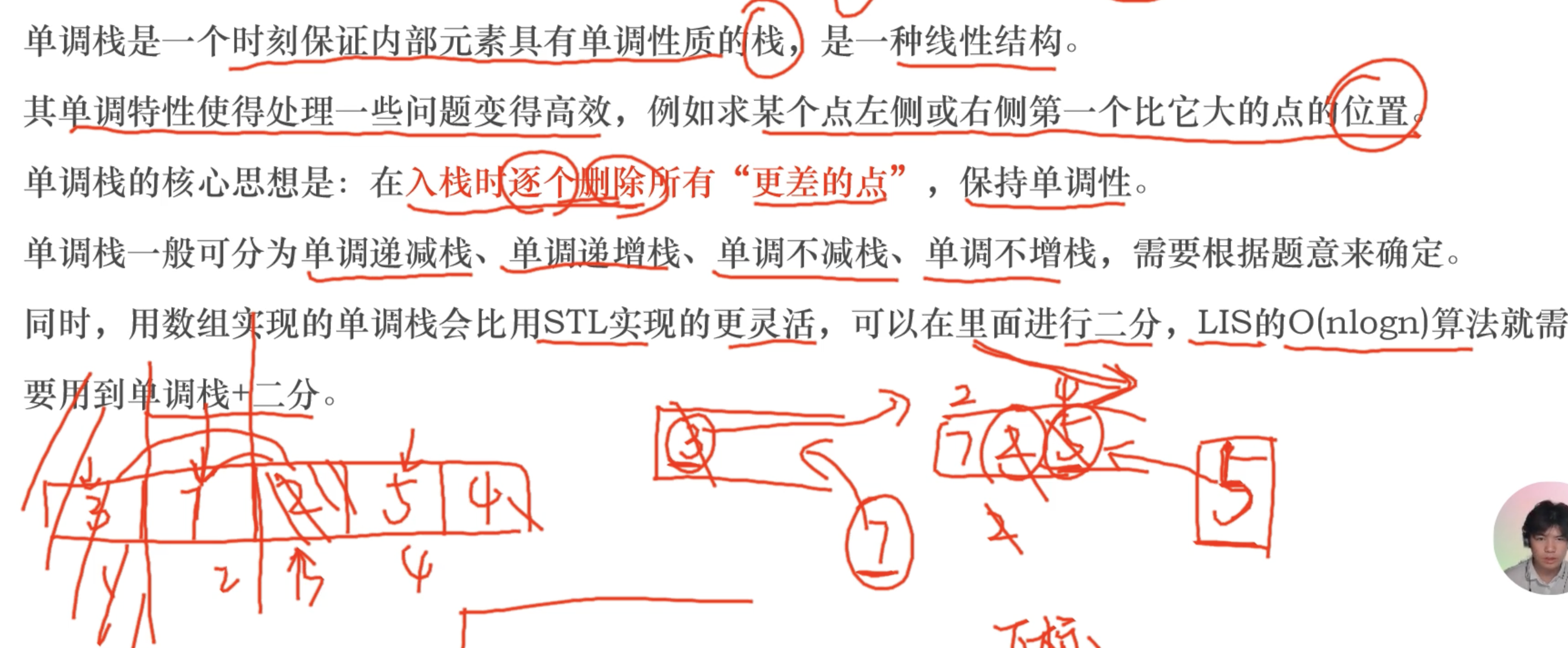
下面会通过几道例题来帮助更好地理解相关内容和知识。

注意⚠️：单调栈常用来作为在固定数组中求解从左边右边比当前元素小（大）的元素坐标，并把坐标存到一个新的数列中，这是单调栈的作用。

问题描述

给定一个长度为 n的序列 Ai​，求 L,R 使 (R−L+1)⋅min⁡(AL,AL+1,…,AR)尽可能大，其中⁡min 表示最小值。

你只需要输出最大的值即可，不需要输出具体的 L,R。

输入格式

输入的第一行包含一个整数 n。

第二行包含 n 个整数，分别表示 A1​,A2​,…,An​，相邻两个整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

输入案例：

5
1 1 3 3 1

输出案例：

5

代码部分：

/*
枚举a[i]作为区间的最小值，我们希望这个区间尽可能的大。
找到a[i]左边第一个小于它的位置l， 和右边第一个小于它的位置r
那么这个区间就是(l, r)
找左（右）边第一个小于它的位置可以使用单调栈来预处理出来
*/#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 3e5 + 9;
int a[N], l[N], r[N];//l[i]表示位置i左边第一个小于它的元素的下标int main()
{int n; cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];stack<int> stk;//对于每个位置找左边（右边）第一个小于它的元素for(int i = 1; i <= n; i++){while(!stk.empty() && a[stk.top()] >= a[i])//栈内单调递增{stk.pop();}if(!stk.empty()){l[i] = stk.top();}else l[i] = 0;stk.push(i);}while(!stk.empty()) stk.pop();for(int i = n; i >= 1; i--){while(!stk.empty() && a[i] <= a[stk.top()]){stk.pop();}if(!stk.empty()){r[i] = stk.top();}stk.push(i);}//枚举每个元素作为区间最小值ll ans = 0;for(int i = 1; i <= n; i++){ans = max(ans, (ll)a[i] * (r[i] - l[i] - 1));}cout << ans << endl;return 0;
}

一、问题本质：为什么要 “固定最小值”？

题目要求最大化 (R-L+1) * min(A[L..R])，这个表达式由两部分构成：

1. 区间长度 (R-L+1)；
2. 区间内的最小值 min(A[L..R])。

这两部分是 “此消彼长” 的关系：区间越长，最小值可能越小；最小值越大，区间可能越短。直接暴力枚举所有区间（O(n²)）会超时，因此需要一种高效的策略 ——枚举每个元素作为 “区间最小值”，计算以它为最小值的最大区间长度，再更新答案。

理由很简单：任何一个区间的最大值，必然对应某个元素作为该区间的最小值。因此，只要枚举所有元素对应的 “最大可行区间”，计算它们的 值×长度，其中的最大值就是答案。

二、关键：如何确定 “以 a [i] 为最小值的最大区间”？

要让 a[i] 成为区间 [L, R] 的最小值，区间内不能有比 a [i] 更小的元素。因此，这个区间的边界由以下两个条件决定：

1. 左边界 L：a [i] 左边第一个小于它的元素的位置 l[i] 的下一个位置（即 L = l[i] + 1）；
2. 右边界 R：a [i] 右边第一个小于它的元素的位置 r[i] 的前一个位置（即 R = r[i] - 1）。

此时，区间 [L, R] 是以 a [i] 为最小值的最大可能区间—— 因为再往左或往右扩展，就会包含比 a [i] 更小的元素，导致 a [i] 不再是区间最小值。

三、用 “左右第一个小于 a [i] 的位置” 确定边界的原理

我们用一个具体例子来解释，假设数组 a = [2, 1, 3, 4, 2]，以 i=3（a [i]=3）为例：

1. 找左边第一个小于 3 的元素：左边元素是 2,1，第一个小于 3 的是 i=2（a=1），因此 l[3] = 2；
2. 找右边第一个小于 3 的元素：右边元素是 4,2，第一个小于 3 的是 i=5（a=2），因此 r[3] = 5；
3. 计算最大区间：左边界 L = l[3]+1 = 3，右边界 R = r[3]-1 =4，区间 [3,4]（元素 3,4）；
4. 验证：区间 [3,4] 的最小值是 3（符合 a [i] 为最小值），且无法再扩展（往左是 1<3，往右是 2<3）。

问题二：

题目描述

这天小明买彩票中了百亿奖金，兴奋的他决定买下蓝桥公司旁的一排连续的楼房。

已知这排楼房一共有 N 栋，编号分别为 1∼N，第 i栋的高度为hi​。

好奇的小明想知道对于每栋楼，左边第一个比它高的楼房是哪个，右边第一个比它高的楼房是哪个（若不存在则输出 −1）。但由于楼房数量太多，小明无法用肉眼直接得到答案，于是他花了 1个亿来请你帮他解决问题，你不会拒绝的对吧？

输入描述

第 1行输入一个整数 N，表示楼房的数量。

第 2 行输入 N个整数（相邻整数用空格隔开），分别为 h1​,h2​,...,hN​，表示楼房的高度。

1≤N≤7×105，1≤hi≤109。

输入案例：

5
3 1 2 5 4 

输出案例：

-1 1 1 -1 4
4 3 4 -1 -1

代码部分：

#include<bits/stdc++.h>
using ll=long long;
using namespace std;
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);ll n;cin>>n;ll a[n+1];for(ll i=1;i<=n;i++)cin>>a[i];stack<ll> s1,s2;ll lans[n+1],rans[n+1];//单调递减序列求左边第一栋for(ll i=1;i<=n;i++){while(!s1.empty()&&a[s1.top()]<=a[i]){s1.pop();}if(s1.empty()){lans[i]=-1;}else{lans[i]=s1.top();}s1.push(i);}//单调递增求右边第一栋for(ll i=n;i>=1;i--){while(!s2.empty()&&a[s2.top()]<=a[i]){s2.pop();}if(s2.empty()){rans[i]=-1;}else{rans[i]=s2.top();}s2.push(i);}for(int i=1;i<=n;i++){cout<<lans[i]<<" ";}cout<<endl;for(int i=1;i<=n;i++){cout<<rans[i]<<" ";}return 0;}

这道题的思路跟上面那道题一样，做这类题目的关键就是要弄清楚，区间内的元素是不变的，也就是数组的元素是固定的。

好了，今天的分享就到这里，希望能对你们有所帮助。