数据结构——二十四、图(王道408)
文章目录
- 前言
- 一.图的定义
- 二.图逻辑结构的应用
- 三.无向图、有向图
- 1.无向图
- 2.有向图
- 四.简单图、多重图
- 1.简单图
- 2.多重图
- 五.顶点的度、入度、出度
- 1.无向图
- 2.有向图
- 六.顶点-顶点的关系描述
- 1.路径
- 2.回路(环)
- 3.简单路径与简单回路
- 4.路径长度
- 5.顶点到顶点的距离
- 6.联通与强联通
- 7.联通图与强联通图
- 1.联通图
- 1.定义
- 2.常考考点
- 2.强联通图
- 1.定义
- 2.常考考点
- 七.研究图的局部——子图
- 1.子图
- 2.生成子图
- 八.连通分量与强连通分量
- 1.连通分量
- 2.强连通分量
- 九.生成树与生成森林
- 1.生成树
- 2.生成森林
- 十.边的权、带权图/网
- 十一.几种特殊形态的图
- 1.无向完全图
- 2.有向完全图
- 3.稀疏图与稠密图
- 4.树,森林,有向树
- 1.树与森林
- 1.概念
- 2.常考考点
- 2.有向树
- 十二.知识回顾与重要考点
- 结语
前言
本文介绍了图的基本概念和逻辑结构。图由顶点集V和边集E组成,分为无向图和有向图。无向图边无序,有向图边有序。简单图不存在重复边和自环边,而多重图允许。顶点的度在无向图中为相连边数,有向图中分为入度和出度。路径分为简单路径和回路,连通性分为连通和强连通。子图包括一般子图和生成子图,连通分量和强连通分量是极大连通子图。连通图的生成树是极小连通子图,非连通图的生成森林由各连通分量的生成树组成。
一.图的定义
- 图G由顶点集V和边集E组成,记为G=(V,E),其中V(G)表示图G中顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合。若V={v1,v2,…,vn}V=\{v_{1},v_{2},\dotsc ,v_{n}\}V={v1,v2,…,vn},则用∣V∣|V|∣V∣表示图G中顶点的个数,也称图G的阶,E={(u,v)∣u∈V,v∈V}E=\{(u,v)\mid u\in V,v\in V\}E={(u,v)∣u∈V,v∈V},用∣E∣|E|∣E∣表示图G中边的条数。
- 注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
二.图逻辑结构的应用
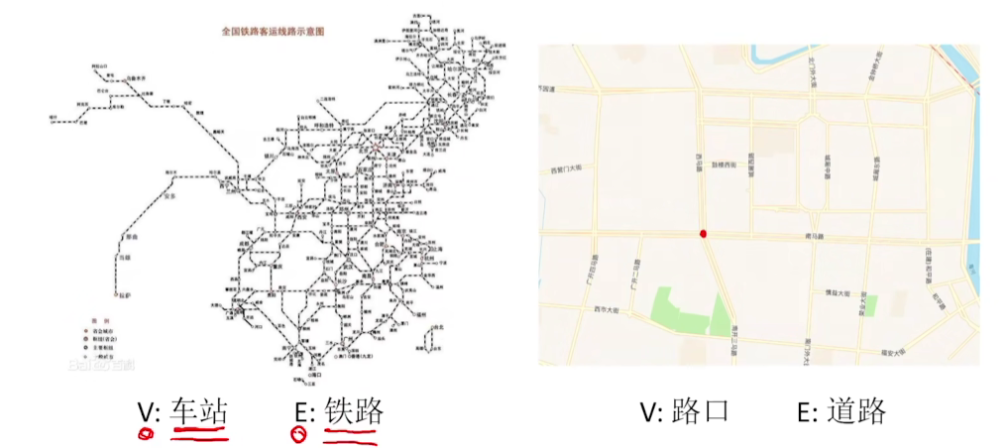
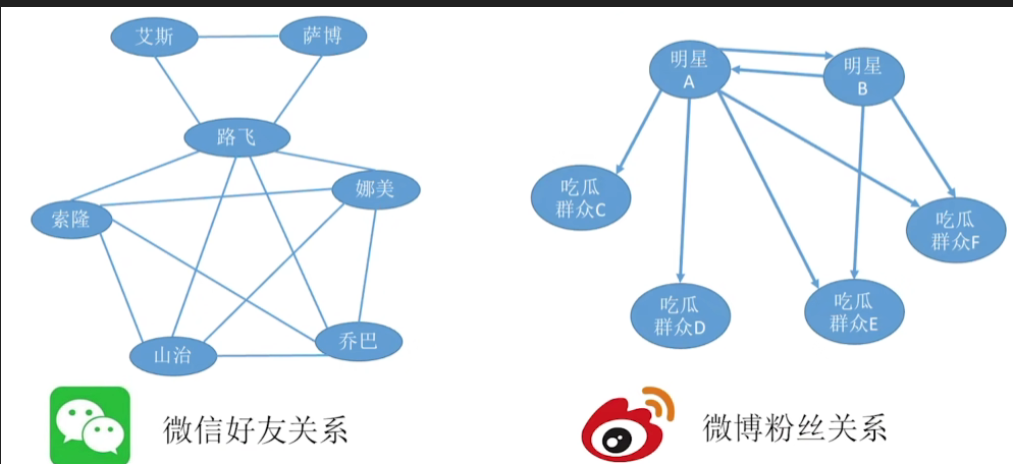
三.无向图、有向图
1.无向图
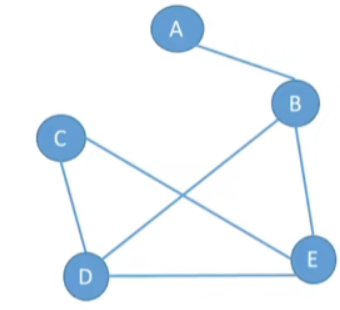
- 若 E 是无向边(简称边)的有限集合时,则图 G 为无向图。边是顶点的无序对,记为 (v,w) 或 (w,v),因为 (v,w)=(w,v),其中 v、w 是顶点。可以说顶点 w 和顶点 v 互为邻接点。边 (v,w) 依附于顶点 w 和 v,或者说边 (v,w) 和顶点 v、w 相关联。
G_{2}=(V_{2},E_{2})
V_{2}={A,B,C,D,E}
E_{2}={(A,B),(B,D),(B,E),(C,D),(C,E),(D,E)}
2.有向图
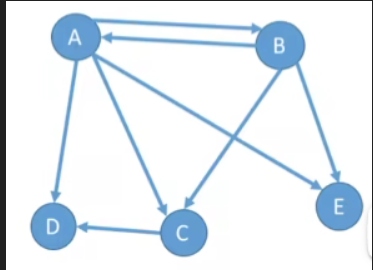
- 若 E 是有向边(也称弧)的有限集合时,则图 G 为有向图。弧是顶点的有序对,记为 <v,w>,其中 v、w 是顶点,v 称为弧尾,w 称为弧头,< v,w> 称为从顶点 v 到顶点 w 的弧,也称 v 邻接到 w,或 w 邻接自 v。<v,m>≠<w,v>
G_{1}=(A,B,C,D,E)
V_{1}={A,B,C,D,E}
E_{1}={< A,B,>,< A,C,>,< A,D,>,< A,E,>,< B,A,>,< B,C,>,< B,E,>,< C,D>}
四.简单图、多重图
数据结构课程只探讨“简单图”
1.简单图
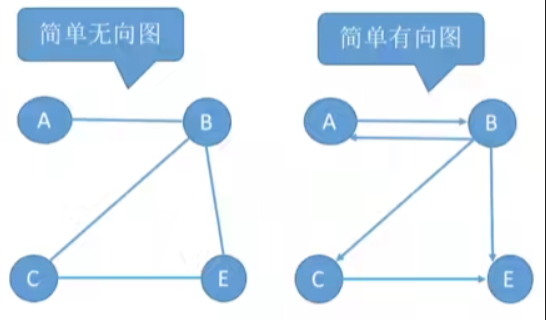
- ①不存在重复边;
- ②不存在顶点到自身的边;
2.多重图
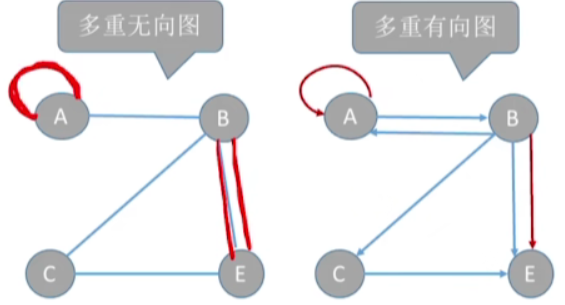
- 图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则G为多重图
五.顶点的度、入度、出度
1.无向图
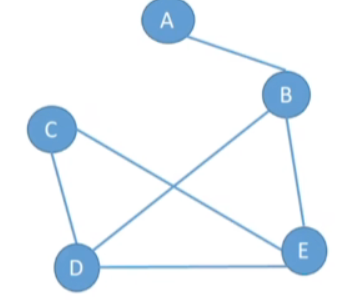
- 对于无向图:顶点v的度是指依附于该顶点的边的条数,记为TD(v)。
- 在具有n个顶点、e条边的无向图中,∑i=1nTD(vi)=2e\sum_{i=1}^{n}\mathrm{TD}(v_{i})=2e∑i=1nTD(vi)=2e
即无向图的全部顶点的度的和等于边数的2倍
2.有向图
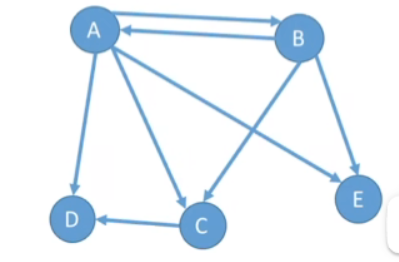
- 对于有向图:
入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v)。 - 顶点v的度等于其入度和出度之和,即TD(v)=ID(v)+OD(v)。
- 在具有n个顶点、e条边的有向图中,∑i=1nID(vi)=∑i=1nOD(vi)=e\sum_{i=1}^{n}ID(v_{i})=\sum_{i=1}^{n}OD(v_{i})=e∑i=1nID(vi)=∑i=1nOD(vi)=e
六.顶点-顶点的关系描述
-
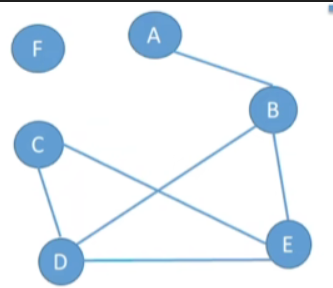
图一
-
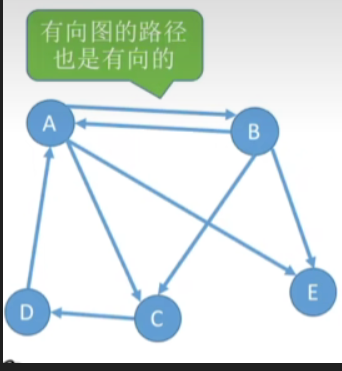
图二
1.路径
-
路径——顶点vpv_{p}vp到顶点vqv_{q}vq之间的一条路径是指顶点序列,vp,vi1,vi2,...,vim,vqv_{p},v_{i_{1}},v_{i_{2}},...,v_{i_m},v_{q}vp,vi1,vi2,...,vim,vq
-
在无向图里边,只要一条边存在,那么你可以从上往下走,也可以从下往上走这个路径的方向是没有限制的,
-
但是在有向图里边,路径的方向必须和弧的方向是一致的
-
如在图一(无向图)中:
- A到D的路径有:
- ABD
- ABED
- ABECD
- A到D的路径有:
-
在图二(有向图)中:
- 顶点A到顶点E的路径:
- ABE
- AE
- 顶点E到顶点A不存在路径
- 顶点A到顶点E的路径:
2.回路(环)
- 回路——第一个顶点和最后一个顶点相同的路径称为回路或环
- 如图一中的BDEB就是一个环
- 如图二中的ABCDA也是一个环
3.简单路径与简单回路
- 简单路径——在路径序列中,顶点不重复出现的路径称为简单路径。
- 简单回路——除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
4.路径长度
- 路径长度——路径上边的数目
5.顶点到顶点的距离
- 点到点的距离——从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离。若从u到v根本不存在路径,则记该距离为无穷(∞)。
6.联通与强联通
- 无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
- 有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的
7.联通图与强联通图
1.联通图
1.定义
- 若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
2.常考考点
-
对于n个顶点的无向图G,
-
若G是连通图,则最少有n-1条边
- 例如5个顶点的最少边数的联通图
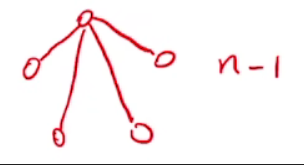
- 例如5个顶点的最少边数的联通图
-
若G是非连通图,则最多可能有Cn−12C_{n-1}^{2}Cn−12条边
- 例如:4个顶点的最大边数的非联通图
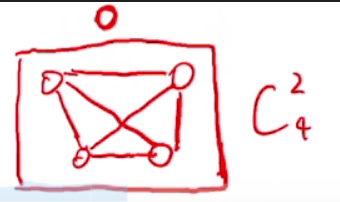
- 例如:4个顶点的最大边数的非联通图
2.强联通图
1.定义
- 若图中任何一对顶点都是强连通的,则称此图为强连通图。
2.常考考点
- 对于n个顶点的有向图G,
- 若G是强连通图,则最少有n条边(形成回路)
- 例如5个顶点边数最少的强联通图
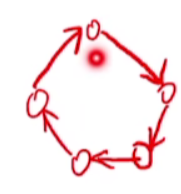
- 例如5个顶点边数最少的强联通图
七.研究图的局部——子图
1.子图
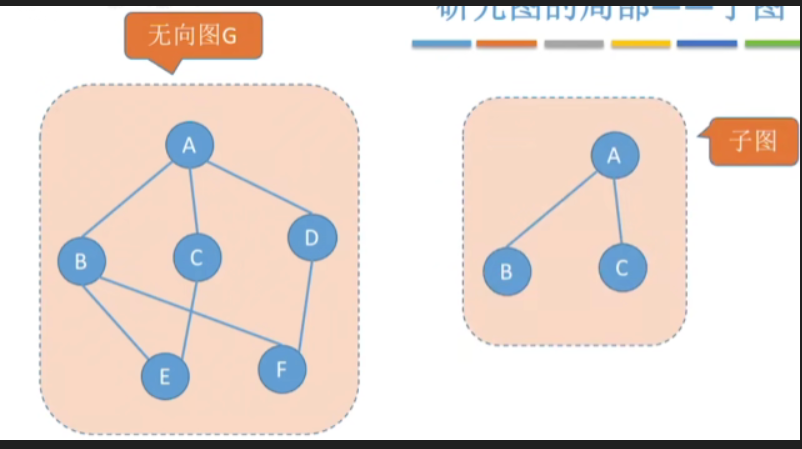
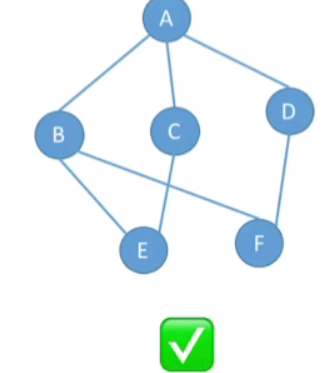
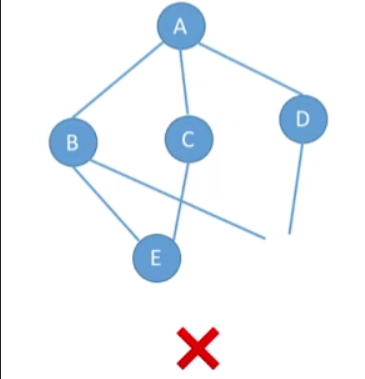
- 设有两个图 G=(V,E) 和 G’=(V’,E’),若 V’ 是 V 的子集,且 E’ 是 E 的子集,则称 G’ 是 G 的子图。
- 并非任意挑几个点、几条边都能构成子图,如下图
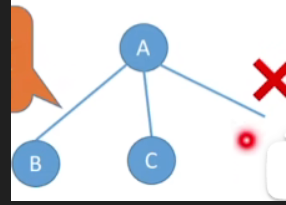
2.生成子图
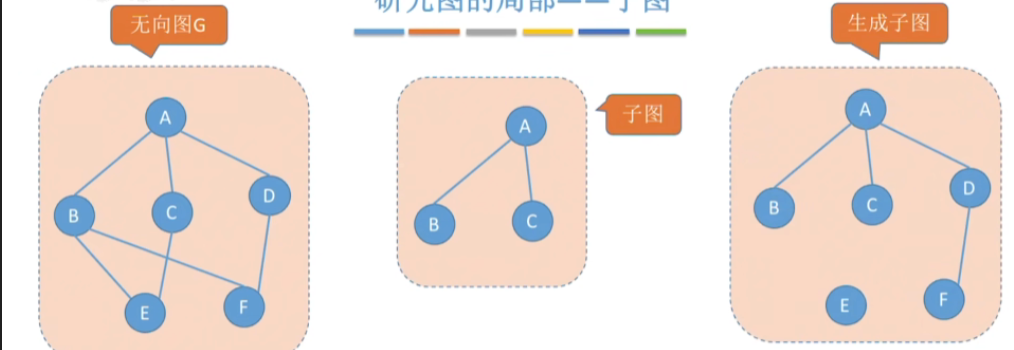
- 若有满足V(G′^{\prime}′)=V(G)的子图G′^{\prime}′,则称其为G的生成子图
- 比如上图中,我们把原图保留全部顶点,去掉了一些边,最后就变成了后面的生成子图
在有向图中,所谓子图和生成子图的概念也是一样的,不再赘述
八.连通分量与强连通分量
1.连通分量
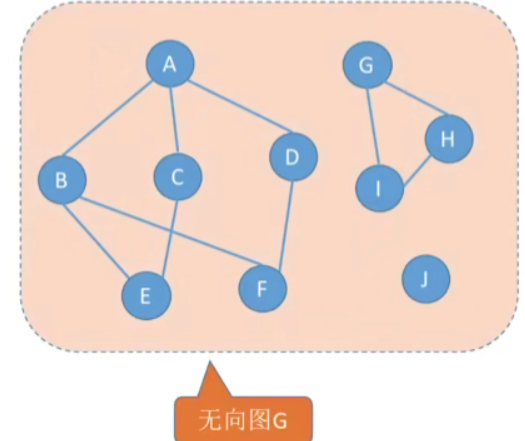
- 无向图中的极大连通子图称为连通分量。
- 极大连通子图:子图必须连通,且包含尽可能多的顶点和边
- 如上图的无向图,我们可以把它分为这样的三个连通分量,每一个连通分量其实都是原图的一个子图,并且这些子图它们都是连通的
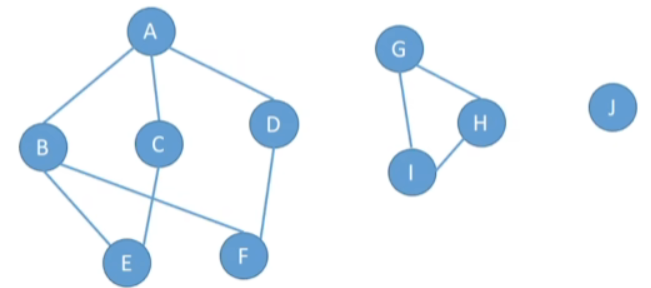
2.强连通分量
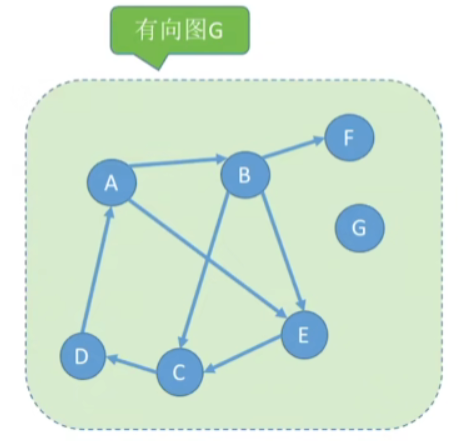
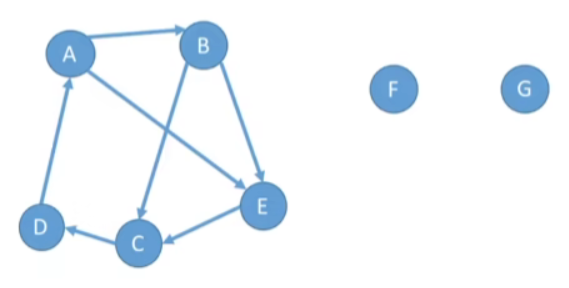
- 有向图中的极大强连通子图称为有向图的强连通分量
- 极大强连通子图:子图必须强连通,同时保留尽可能多的边
- 如上面的有向图中,强连通分量有:
九.生成树与生成森林
1.生成树
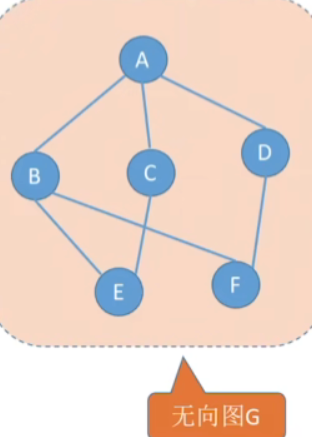
-
连通图的生成树是包含图中全部顶点的一个极小连通子图。
-
极小连通子图:边尽可能的少,但要保持连通
-
如上图的生成树为:
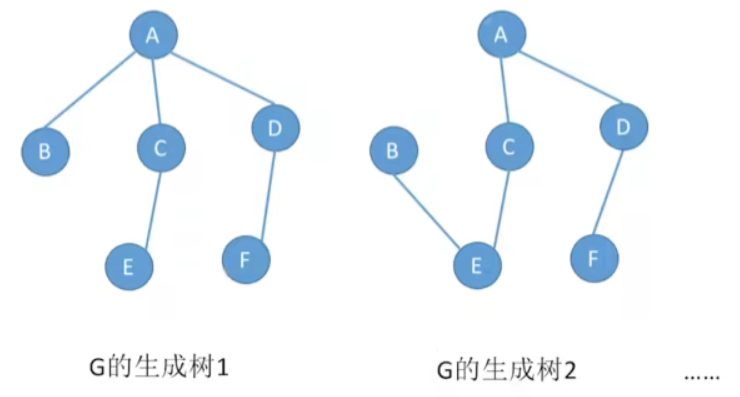
-
若图中顶点数为n,则它的生成树含有n-1条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
2.生成森林
-
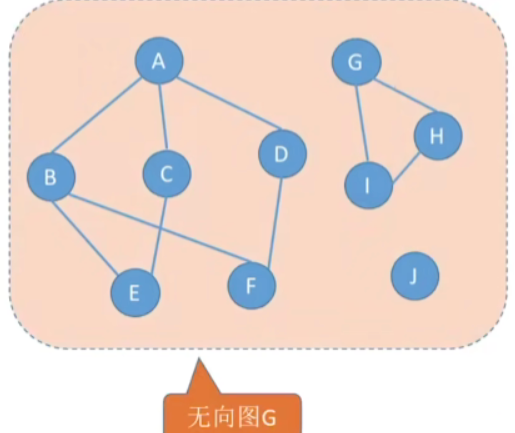
在非连通图中,连通分量的生成树构成了非连通图的生成森林。
-
如上非连通无向图,先将其所有的连通分量画出来
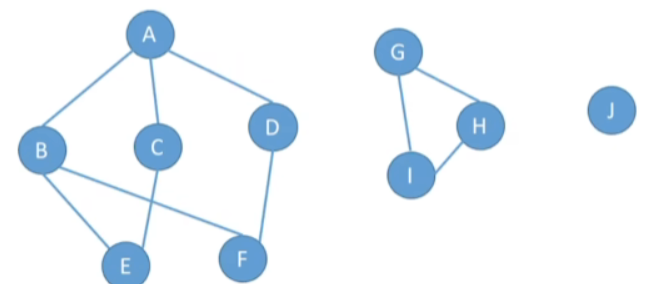
-
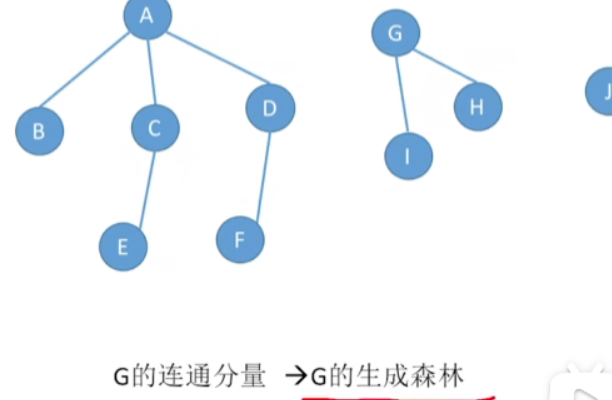
然后将其全部转化为生成树,就变成了生成森林
十.边的权、带权图/网
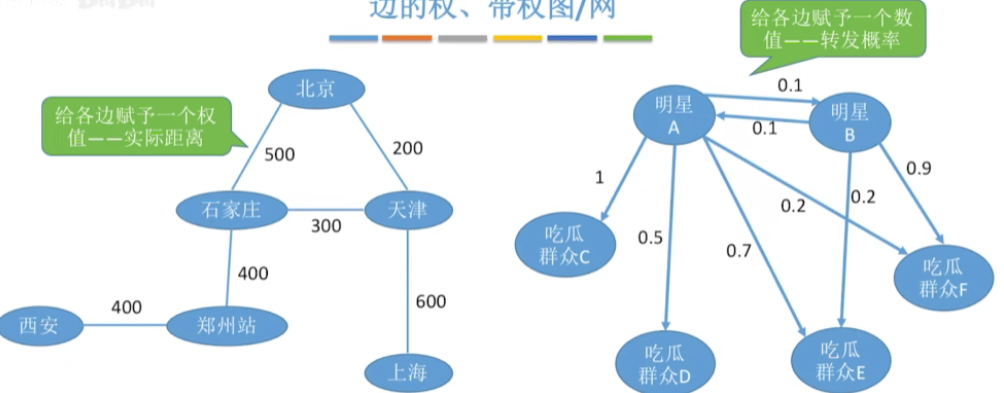
- 边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。带权图/网——边上带有权值的图称为带权图,也称网。
- 带权路径长度——当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
十一.几种特殊形态的图
1.无向完全图
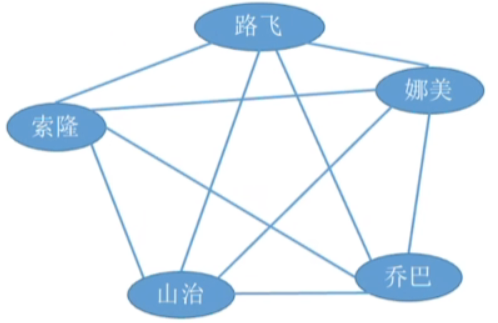
- 无向完全图—无向图中任意两个顶点之间都存在边
- 若无向图的顶点数 |V|=n,则∣E∣∈[0,Cn2]=[0,n(n−1)/2]|E|\in[0,C_{n}^{2}]=[0,n(n-1)/2]∣E∣∈[0,Cn2]=[0,n(n−1)/2]
2.有向完全图
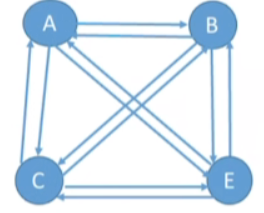
- 有向完全图—有向图中任意两个顶点之间都存在方向相反的两条弧
- 若有向图的顶点数∣V∣=n\mid V\mid=n∣V∣=n ,则∣E∣∈[0,2Cn2]=[0,n(n−1)]\mid E\mid \in\left[0,2C_{n}^{2}\right]=\left[0,n(n-1)\right]∣E∣∈[0,2Cn2]=[0,n(n−1)]
3.稀疏图与稠密图
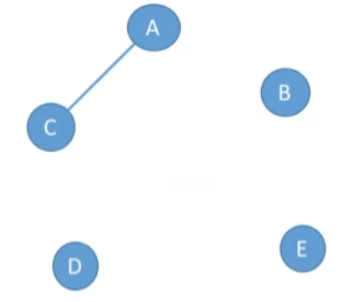
- 边数很少的图称为稀疏图
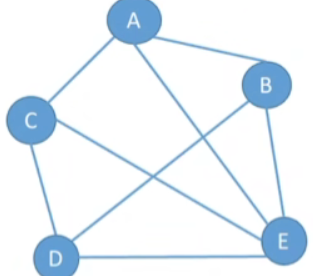
- 反之称为稠密图
没有绝对的界限,一般来说|E|<|V|log|V|时,可以将G视为稀疏图
4.树,森林,有向树
1.树与森林
1.概念
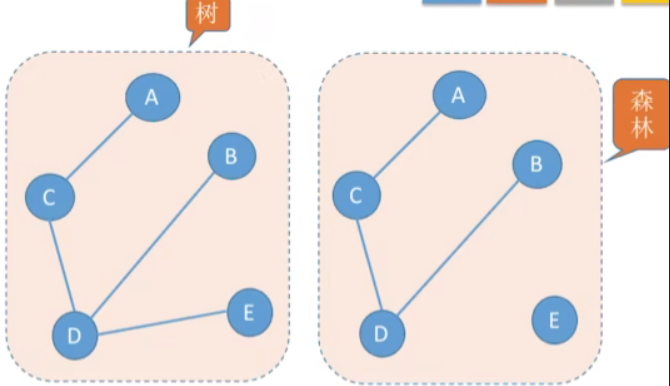
- 树–不存在回路,且连通的无向图
- n个顶点的树,必有n-1条边。
2.常考考点
- n个顶点的图,若|E|>n-1,则一定有回路
2.有向树
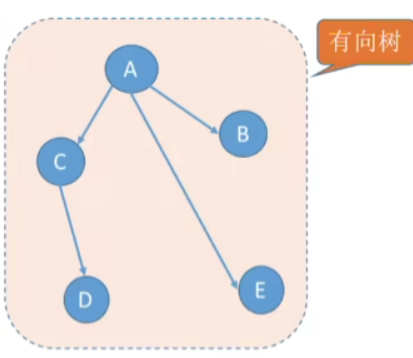
- 有向树——一个顶点的入度为0、其余顶点的入度均为1的有向图,称为有向树。
十二.知识回顾与重要考点

结语
终于到图了,没想到能坚持这么久,接下来我还要继续努力啊😉
如果想查看更多章节,请点击:一、数据结构专栏导航页
