《小白学随机过程》第一章：随机过程——定义和形式

1.历史背景

从布朗运动到维纳过程

1. 1827年：英国植物学家罗伯特·布朗（Robert Brown）在显微镜下观察花粉颗粒在水中的运动，发现这些微小颗粒并非静止，而是在做无规则、连续、永不停止的抖动。并且有以下观察，当时 Brown 无法解释原因，以为是“生命活力”，但后来发现无机灰尘颗粒也有同样现象。这种现象后来被称为“布朗运动”。
   • 运动与颗粒大小有关（越小越剧烈）；
   • 与液体温度有关（温度越高越剧烈）；
   • 与颗粒材质无关（非生命现象）
2. 1905年：爱因斯坦从统计力学角度解释布朗运动，指出这是由于液体分子对微粒的随机碰撞所致，并预测位移服从正态分布。
   • 悬浮微粒受到周围液体分子大量、频繁、随机的碰撞。
   • 每次碰撞带来微小位移，方向和大小都随机
   • 在时间间隔 $\Delta t$ 内，微粒的总位移是大量微小独立随机位移的和
   • 中心极限定理（CLT）登场：大量独立同分布（或弱相关）随机变量之和，近似服从正态分布。
3. 1923年：美国数学家诺伯特·维纳（Norbert Wiener）首次严格地从数学上构建了描述布朗运动的连续时间随机过程，因此该过程也被称为“维纳过程”(随机过程的一种类型)

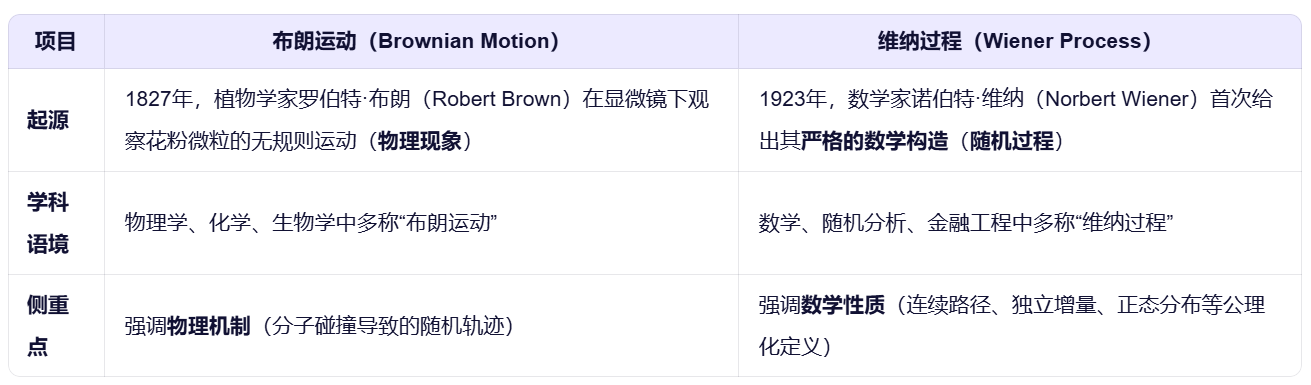
布朗运动、维纳过程的关系

维纳过程是布朗运动的严格数学定义；布朗运动是维纳过程所描述的物理现象。在当代数学、金融、工程等领域，“布朗运动”与“维纳过程”通常视为同义词。

2. 从概率论到随机过程

下面我们将从概率论与随机变量的起点出发，逐步阐明为什么需要引入随机过程，并系统对比二者的异同点与适用场景。

---

2.1 起点：概率论与随机变量（静态不确定性）

2.1.1 概率论的核心对象：随机变量

在概率空间 $(\Omega ,\mathcal{F},P)$ 上，随机变量是一个可测函数：
$$X:\Omega \to \mathbb{R},\omega \mapsto X(\omega )$$

它将样本空间中的每个基本结果 $\omega$ 映射为一个实数，用于量化单次随机试验的结果。

理解随机变量含义非常重要，请参考这里(重要)
这里有对上述公式更进一步的解读，仅供参考

2.1.2 典型例子

• 掷一枚骰子的点数： X ∈ { 1 , 2 , 3 , 4 , 5 , 6 } X \in \{1,2,3,4,5,6\} X∈{1,2,3,4,5,6}
• 明日是否下雨：$X=\{\begin{array}{ll}1& \text{下雨}\\ 0& \text{不下雨}\end{array}$
• 某股票明日收盘价：$X\in {\mathbb{R}}^{+}$

2.1.3 随机变量能解决的问题（静态视角）

• 概率计算：$\mathbb{P}(X>5)$
• 期望与方差：$\mathbb{E}[X],\text{Var}(X)$
• 多变量关系：协方差 $\text{Cov}(X,Y)$、相关性

✅ 核心特征：关注单一时点或孤立事件的不确定性，不涉及时间演化或历史依赖。

---

2.2 现实挑战：动态不确定性无处不在

许多实际系统具有以下特征：

• 随时间连续演化（如股价、气温、网络流量）
  • 气温为例：今天平均气温30度，则明天的平均气温极有可能在30度附近。今天的气温$X$和明天的$X$具有一定演化过程，不是完全孤立的
• 当前状态受历史影响（如天气、语音信号）
• 路径本身具有统计规律（如布朗粒子的轨迹）

❗ 问题：仅用一个或几个随机变量无法描述“整个演化过程”或“轨迹行为”。

例如：

• 问：“未来5天每天是否下雨？” → 需要5个相关随机变量 $X_1,X_2,\dots ,X_5$
• 问：“股价是否会跌破某阈值？” → 需要分析整个路径 { S ( t ) : 0 ≤ t ≤ T } \{S(t): 0 \leq t \leq T\} {S(t):0≤t≤T}

这就要求我们将时间纳入建模框架。

---

2.3 解决方案：引入随机过程（动态不确定性建模）

2.3.1 随机过程的定义

随机过程是一族依赖于参数（通常是时间 $t$）的随机变量：
{ X ( t ) : t ∈ T } \{X(t) : t \in T\} {X(t):t∈T}
其中：

• $T$ 是指标集（如 $T=\mathbb{N}$ 表示离散时间，$T=[0,\infty )$ 表示连续时间）；
• 对每个固定的 $t$，$X(t)$ 是一个随机变量；
• 对每个固定的 $\omega \in \Omega$，函数 $t\mapsto X(t,\omega )$ 称为一条样本路径（sample path） 或实现（realization）。

这里的定义和这个链接讲述的公式定义本质是一样的，公式定义更标准、凝练

2.3.2 随机过程能回答的问题（动态视角）

• “过程是否会在某时刻首次达到某值？”（首达时间）
• “给定过去，未来如何分布？”（马尔可夫性、预测）
• “路径是否连续？是否具有周期性？”（路径性质）
• “长期平均行为如何？”（遍历性、平稳性）

---

2.4 随机变量 vs 随机过程：异同点对比

• 不同点：

维度	随机变量	随机过程
数学对象	单个可测函数 $X:\Omega \to \mathbb{R}$	一族可测函数 { X ( t ) } t ∈ T \{X(t)\}_{t \in T} {X(t)}t∈T​
时间角色	无时间概念，或仅单一时点	时间（或空间）是核心索引
样本表现	一个数值	一条函数曲线（如股价走势图）
依赖结构	多个变量可相关，但无序贯演化	显式建模不同时刻的统计依赖（如自相关、马尔可夫性）
理论工具	分布函数、矩、特征函数	有限维分布族、协方差函数、谱分析、鞅、随机微分方程
典型问题	“结果是多少？”	“过程如何演化？路径有何性质？”

• 相同点：
  • 都基于同一概率空间 $(\Omega ,\mathcal{F},P)$；
  • 都用概率分布描述不确定性；
  • 随机过程在固定时间点的取值就是一个随机变量。

📌 关系：随机过程是随机变量的自然推广；随机变量是随机过程的单点切片。

---

2.5 适用场景对比

2.5.1 随机变量适用场景（静态/孤立事件）

场景	示例
单次试验	投硬币、抽签、一次质检结果
横截面数据	调查1000人的身高（假设独立）
单点风险评估	某资产明日亏损超10%的概率
基础概率模型	二项分布（n次独立试验成功次数）、泊松分布（单位时间事件数）

✅ 关键：不关心历史，也不预测未来轨迹。

2.5.2 随机过程适用场景（动态/演化系统）

场景	典型模型	应用领域
金融时间序列	几何布朗运动、GARCH	股票定价、风险管理
通信与网络	泊松过程、M/M/1 队列	数据包到达建模、带宽分配
信号处理	平稳高斯过程、ARMA	语音/图像去噪、谱估计
状态转移系统	马尔可夫链（离散/连续时间）	语音识别、搜索引擎（PageRank）
物理扩散现象	布朗运动（维纳过程）	分子运动、热传导
空间随机现象	高斯随机场、马尔可夫随机场	医学图像分割、地质建模
智能决策	马尔可夫决策过程（MDP）	强化学习、机器人路径规划

✅ 关键：必须建模“时间（或空间）中的不确定性演化”。

2.6 直观类比

概念	类比
随机变量	一张照片：捕捉某一瞬间的状态
随机过程	一部电影：包含无数帧（随机变量），且帧与帧之间有剧情（依赖关系）

即使你有1000张独立的照片（i.i.d. 随机变量），也无法还原出电影的连贯动作——动态依赖结构才是核心。

2.7 总结：为何引入随机过程？

问题	回答
概率论和随机变量不够用吗？	对静态或独立重复实验足够，但对动态、相关、演化系统无能为力。
引入随机过程解决了什么？	提供了描述和分析随时间（或空间）演化的随机现象的统一数学框架。
二者关系？	随机变量是“点”，随机过程是“轨迹”；后者是前者的自然推广。
如何选择？	• 若只关心单次结果或独立重复 → 用随机变量； • 若关心路径、趋势、记忆、预测 → 必须用随机过程。

🌟 终极理解：
概率论处理“不确定性”，随机过程处理“时间中的不确定性”。
从随机变量到随机过程，是概率论从静态世界走向动态世界的伟大跨越。