[优选算法专题四.前缀和——NO.25一维前缀和]
题目链接:
一维前缀和
题目描述:
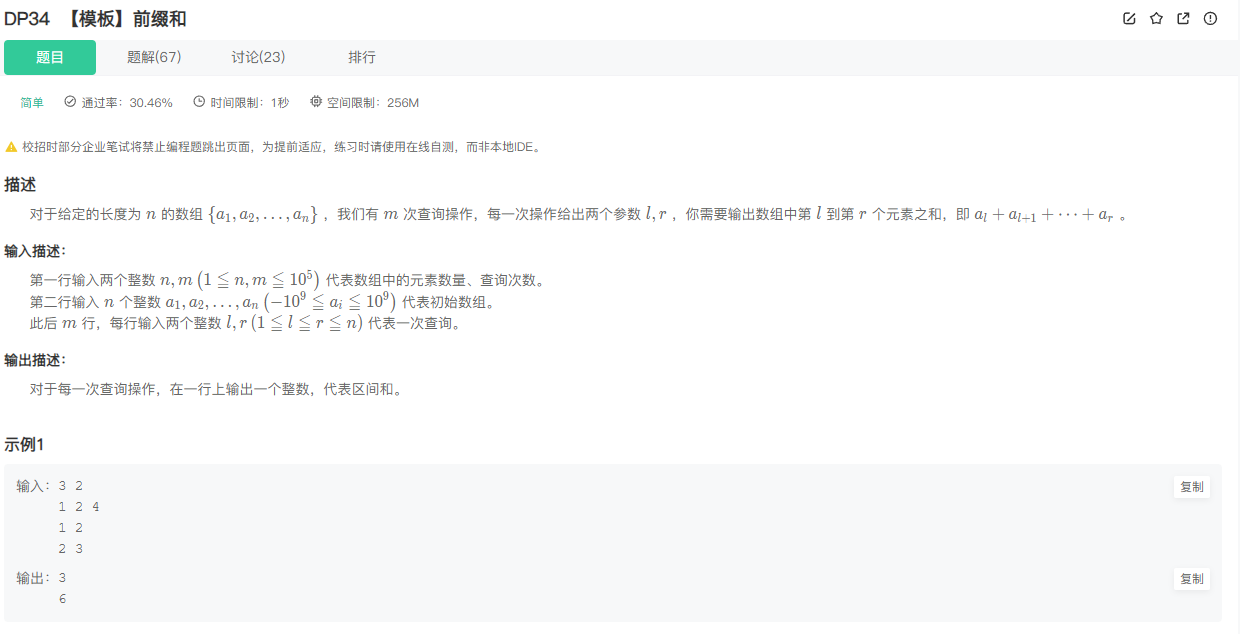
题目解析:
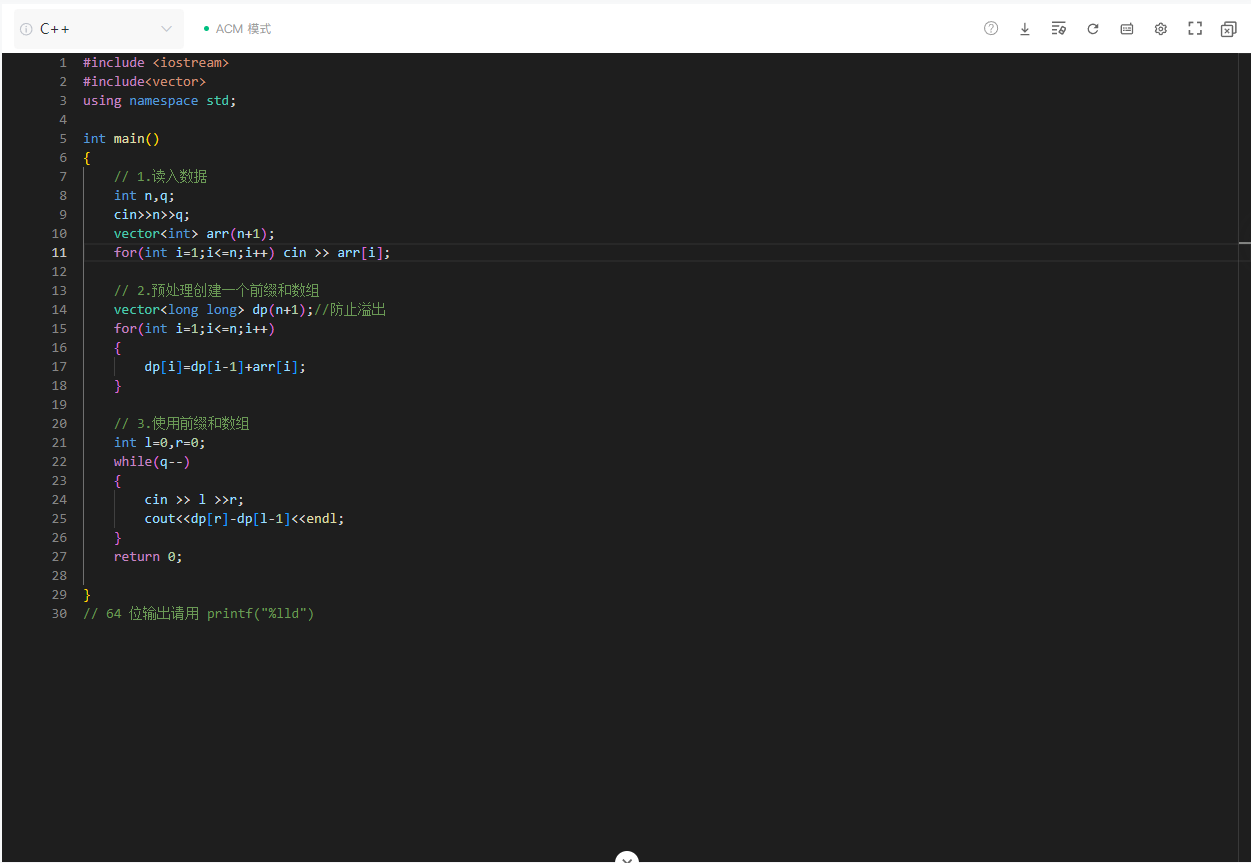
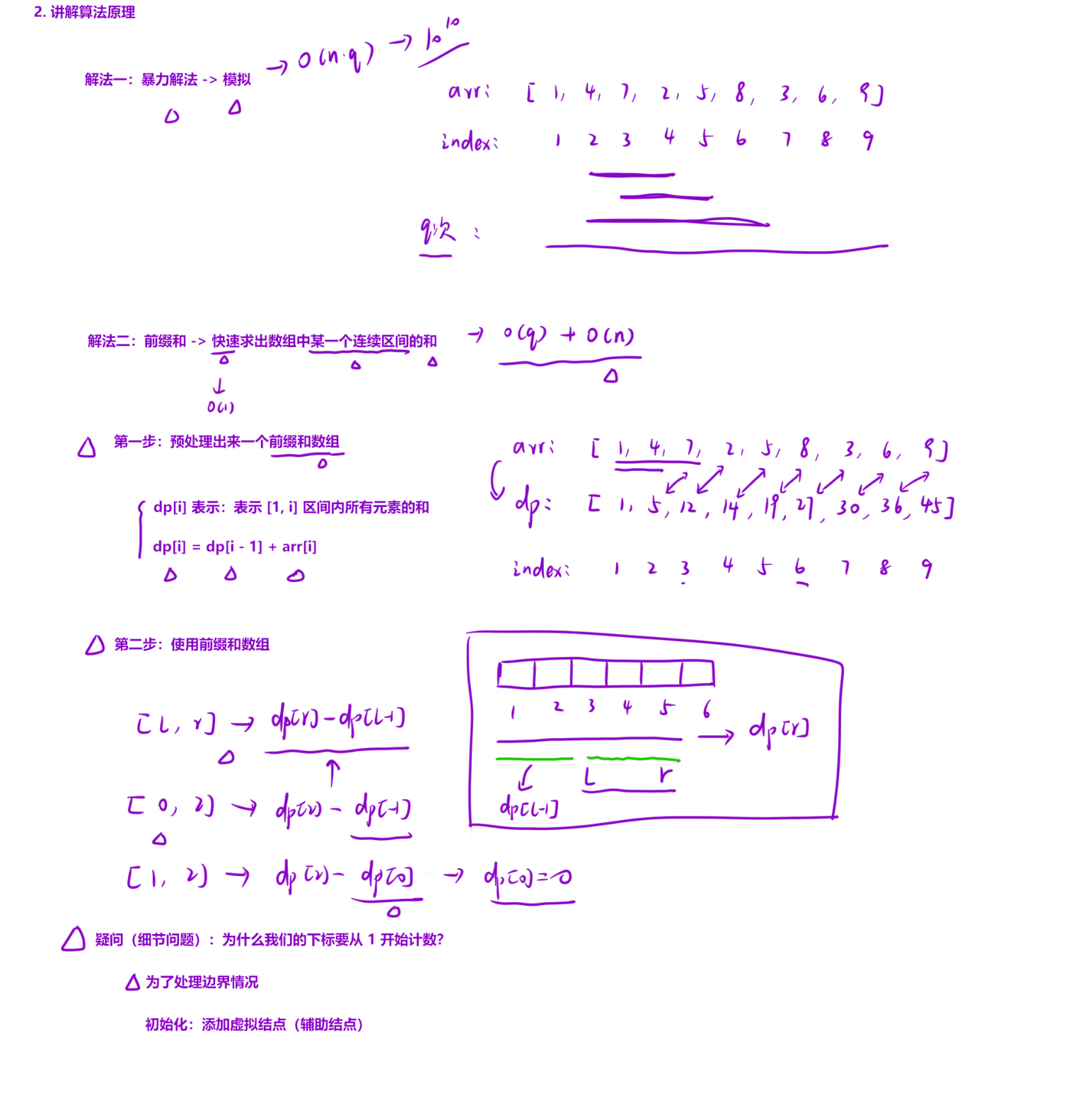
代码逐部分解析
读取输入数据
int n, q; cin >> n >> q; vector<int> arr(n + 1); // 数组下标从1开始(便于前缀和计算) for (int i = 1; i <= n; i++) cin >> arr[i];
n表示数组的长度,q表示查询的次数。- 定义
arr数组时大小为n+1,且从下标1开始存储元素(而非 0),这是为了后续前缀和计算更方便(避免处理i=0的边界问题)。
构建前缀和数组dp
vector<long long> dp(n + 1); // 用long long防止整数溢出 for (int i = 1; i <= n; i++) {dp[i] = dp[i - 1] + arr[i]; }
dp是前缀和数组,其中dp[i]表示arr[1] + arr[2] + ... + arr[i]的和。- 采用
long long类型是为了避免当数组元素较大或n较大时,累加和超过int的范围导致溢出。- 递推关系:
dp[i] = dp[i-1] + arr[i],即前i个元素的和 = 前i-1个元素的和 + 第i个元素。
处理区间和查询
int l = 0, r = 0; while (q--) {cin >> l >> r;cout << dp[r] - dp[l - 1] << endl; }
- 每次查询输入区间
[l, r],需要计算arr[l] + arr[l+1] + ... + arr[r]。- 利用前缀和数组的性质:区间
[l, r]的和 = 前r个元素的和 - 前l-1个元素的和,即dp[r] - dp[l-1]。- 这种查询方式的时间复杂度是
O(1),配合预处理的O(n)时间,整体效率远高于每次查询都遍历区间的O(n*q)复杂度,尤其适合q较大的场景。
注意:为什么下标要从一开始❓
1. 前缀和公式更直观
前缀和数组
dp[i]的定义是 “前i个元素的和”(即arr[1] + arr[2] + ... + arr[i])。当计算区间[l, r]的和时,公式为:区间和 = dp[r] - dp[l-1]如果下标从 1 开始:
- 当
l=1时,l-1=0,而dp[0]可以自然定义为0(前 0 个元素的和),此时公式变为dp[r] - dp[0],直接等于arr[1]到arr[r]的和,无需额外处理边界。2. 避免下标越界或特殊判断
如果下标从 0 开始:
- 前缀和
dp[0]表示arr[0]的和,dp[i] = dp[i-1] + arr[i]。- 当查询区间
[0, r]时,区间和需要用dp[r] - dp[-1],但dp[-1]是无效下标(越界),此时必须单独判断l=0的情况(比如让dp[-1]等价于 0),会增加代码复杂度。
