告别炼丹玄学：用元学习精准预测模型性能与数据需求，AWS AI Lab研究解读

摘要: 在AI项目立项时，你是否也曾被灵魂拷问：“需要多少数据才能达到95%的准确率？” 这个问题以往常常依赖经验甚至“玄学”。今天，我们深入解读一篇来自AWS AI Lab的前沿论文《A Meta-Learning Approach to Predicting Performance and Data Requirements》，它提出了一种名为“分段幂律 (PPL)”的方法，结合元学习，旨在将数据需求的预测从艺术变为科学，帮助我们节省数百万的标注成本。

---

一、AI项目经理的噩梦：预测失准的“幂律”

长期以来，学术界和工业界都依赖一个公认的准则——幂律 (Power Law) 来预测模型的学习曲线。简单来说，它认为模型的性能（如错误率）会随着数据量的增加，在对数坐标下呈现出一条平滑的直线。

这意味着，我们只需要用少量数据跑几个实验点，就能“画一条直线”，然后“外推”出未来的性能。

听起来很美好，但现实很残酷。

论文一针见血地指出：在数据量极少的小样本 (few-shot) 阶段，学习曲线根本不是一条直线！它更像一条陡峭的弧线。如果强行用直线去拟合，就会像下图一样，导致预测结果严重失准。

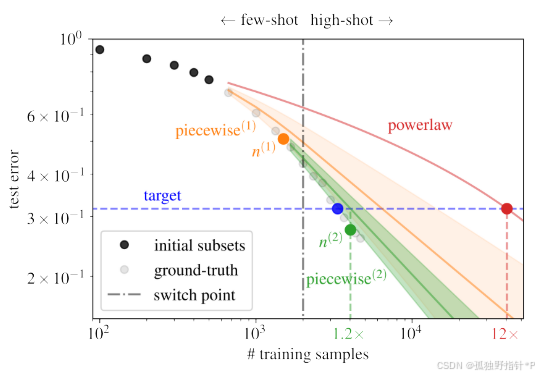
图1解读: 传统幂律（powerlaw）预测达到目标（target）需要的数据量是真实需求的12倍，而论文提出的新方法分两步预测，最终误差仅为1.2倍，极大地避免了成本浪费。

这种巨大的高估，在实际项目中可能是灾难性的，可能导致项目预算超支甚至直接被砍。

二、更聪明的模型：分段幂律 (PPL)

为了解决这个问题，作者提出了一个更符合真实学习规律的模型——分段幂律 (Piecewise Power Law, PPL)。

其核心思想非常直观，就像运动员的成长分为两个阶段：

1. 新手黄金期 (Few-shot, n < N): 进步神速，成绩提升是一条陡峭的曲线。PPL使用二次函数来精确建模这个阶段。
2. 高手瓶颈期 (High-shot, n > N): 进步变得平稳且缓慢，成绩提升更像一条平缓的直线。PPL使用线性函数来建模。

这个模型的关键在于找到那个从“新手”到“高手”的切换点N。

---

三、点睛之笔：如何找到“切换点N”？

要在数据极少的情况下精确找到“切换点N”是非常困难的。为此，作者引入了本文的“独门秘籍”——元学习 (Meta-Learning)。

他们训练了一个随机森林回归器，就像聘请了一位经验丰富的“传奇向导”。这位向导“见过”成百上千个不同项目的学习曲线，积累了丰富的“元知识”。我们只需要把项目最初的几个性能点（初始学习曲线）和任务信息（如类别数）喂给它，它就能凭借经验，直接预测出最可能的“切换点N”。

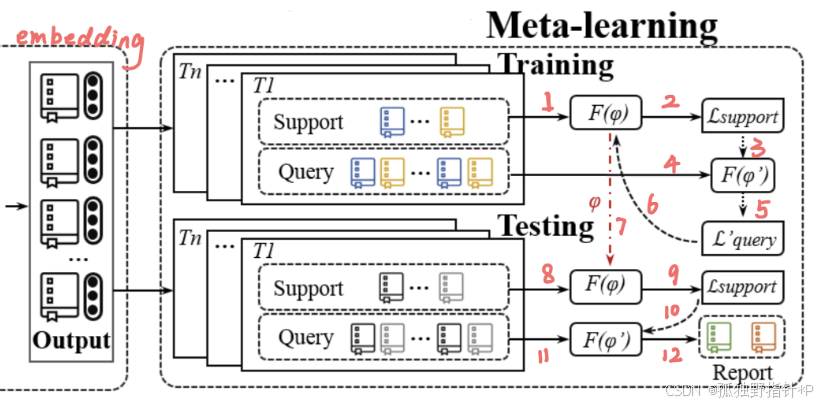
在确定了N之后，再使用 Levenberg-Marquardt 算法进行精确的曲线拟合，并引入置信度边界来制定稳健的、分步走的预测策略，避免“一步错，步步错”。

四、效果炸裂：实验结果展示

Talk is cheap, show me the data. 论文在16个分类和10个检测任务上进行了详尽的实验，结果令人信服。

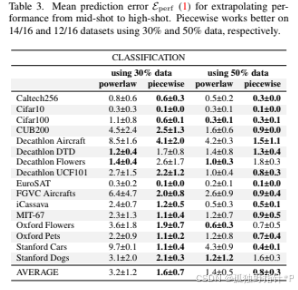
1. 性能预测误差 (${\mathcal{E}}_{perf}$)

与传统方法相比，PPL的预测误差显著降低。

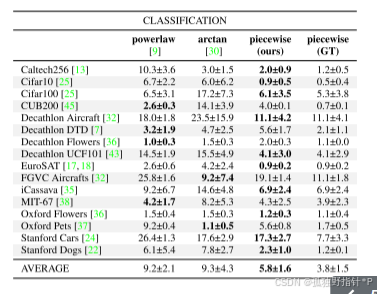
分类任务 (平均误差对比):

在16个分类任务上，PPL平均误差为5.8，相比幂律的9.2，降低了37%。

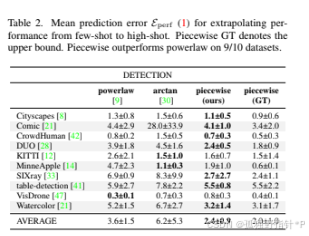
物体检测任务 (平均误差对比):

在10个检测任务上，PPL平均误差为2.4，相比幂律的3.6，降低了33%。

2. 数据需求量估算误差 (${\mathcal{E}}_{data}$)

这是衡量模型实用价值的核心指标。结果显示，PPL完美解决了传统方法严重高估的问题。

结果解读: 传统幂律（powerlaw）的预测误差动辄几十倍，甚至出现无穷大（inf）。而作者的最佳策略（piecewise 5-step 5%）的误差始终稳定在0附近，几乎是完美预测，平均将数据预估误差减少了76%（分类）和91%（检测）。

3. 强大的泛化与鲁棒性

更厉害的是，这个模型不是“纸上谈兵”的理论模型，它拥有极强的泛化能力。

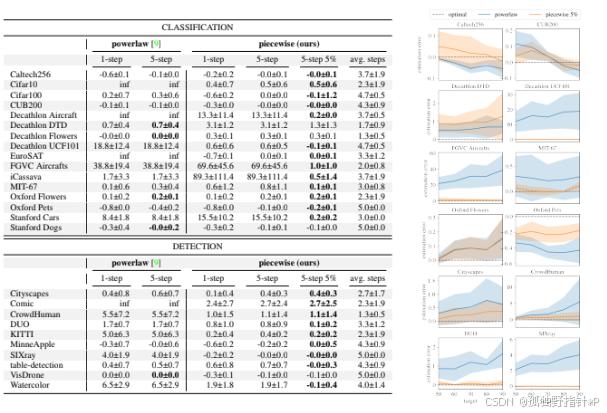
实验证明，在ResNet-18上训练的元模型，可以无缝迁移到更复杂的ResNet-50、全新架构的ViT，以及线性探测等不同场景下，表现依旧出色。

同时，模型对“切换点N”的预测误差有很高的容忍度，即便“向导”偶尔指错路，最终结果也比传统方法好得多，证明了其鲁棒性。

五、总结

这篇论文为AI工程化解决了一个非常实际且头疼的问题。它告诉我们：

1. 别再迷信单一的幂律：尤其是在小样本阶段，它真的不准。
2. 分阶段建模是关键：PPL模型更符合真实世界的学习规律。
3. 元学习是强大的工具：它能让模型“举一反三”，从过去的经验中为新任务提供宝贵的先验知识。

通过这种“精确模型 + 经验指导 + 稳健策略”的组合拳，我们可以更科学地规划AI项目，将宝贵的资源用在刀刃上，真正地告别“炼丹玄学”。

强烈推荐所有从事AI项目管理和算法工程的同学阅读原文，获取更多技术细节！论文及其代码连私信获取