反常积分的判敛散

1.基本思想

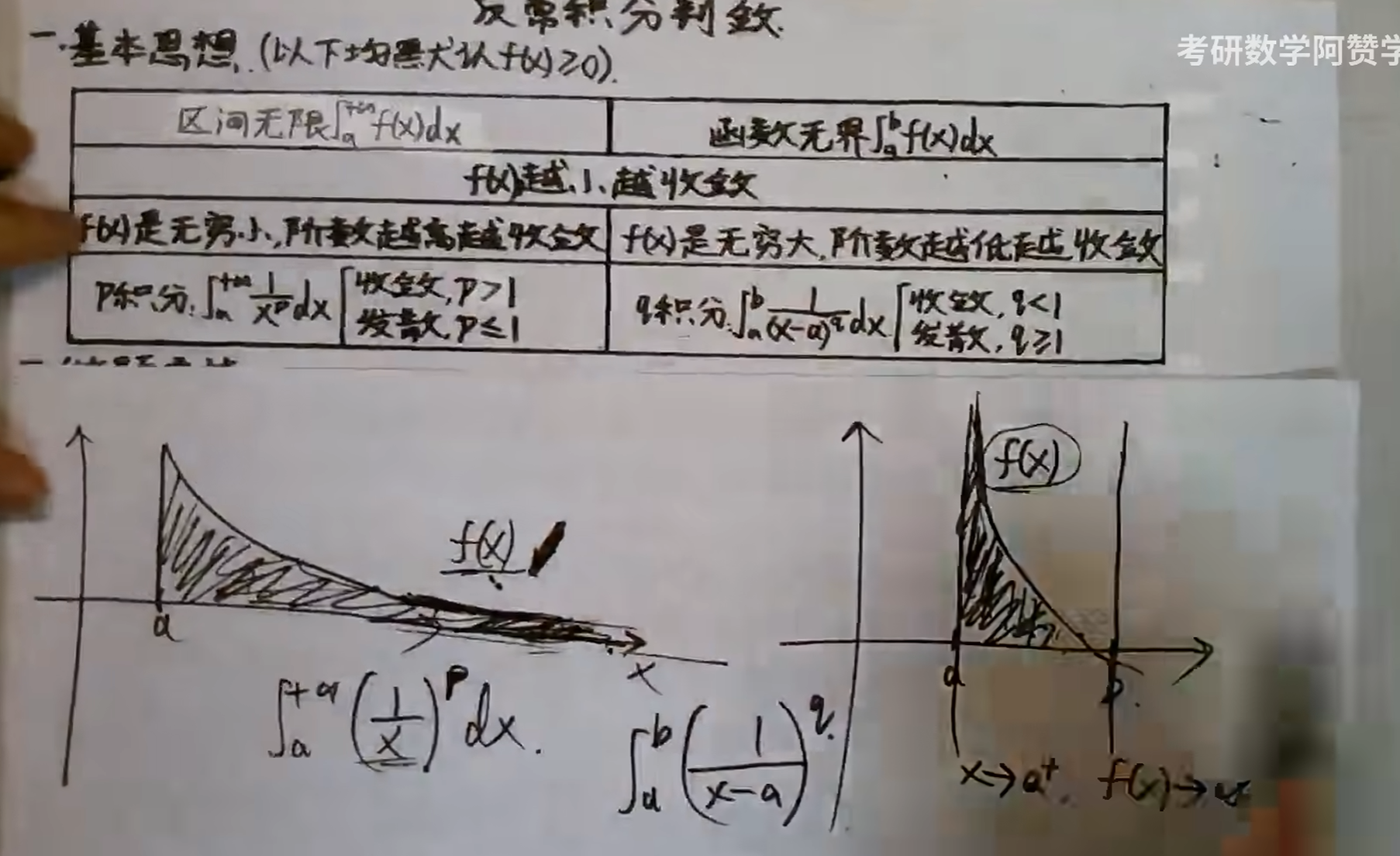
这里就运用了等价的思想，区间上0，+∞

有两个瑕点，所以分成了两个区间，分别判断，一个是p积分

一个是q积分，分别抓对应的大头，然后就可以判断敛散性，收加收就是收

2.注意凑成q积分时其指数需要在括号外面

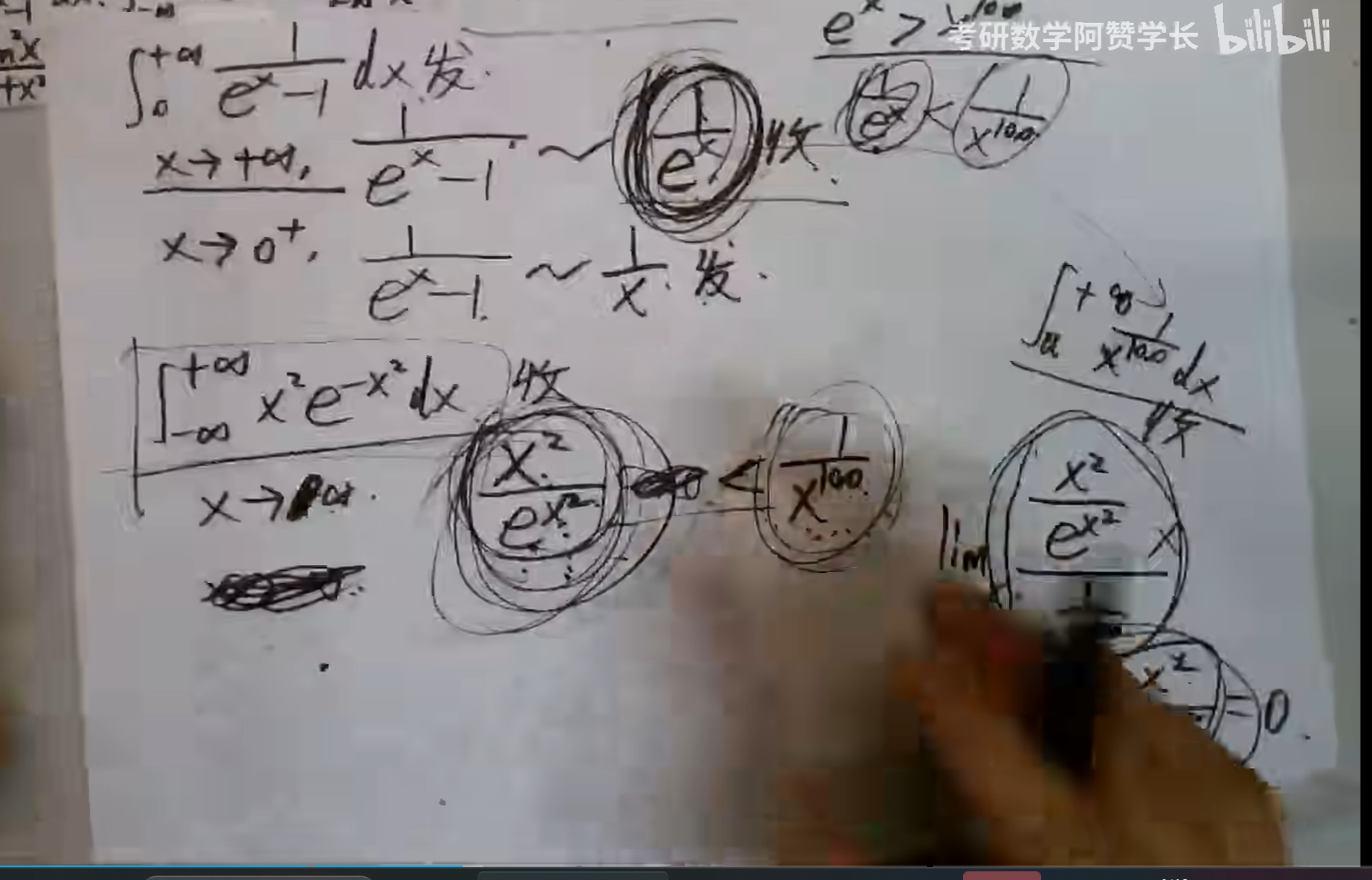
3.指数形式

远大于x

4对数形式

敛散性的判别本质是比大小

指数在上时

无视lnx即可

指数单独在分母时

当趋于无穷时，lnx他远小于x所以他一定发散，应为太大了

当x->常数时，lnx他->无穷的速度太慢了，所以他一定收敛

当分母同时存在x和对数

先判断x上的指数是不是=1，如果≠1那么直接无视ln，如果等于1那么直接进行积分变成∫(lnx)的1-a次方，当a＞1时，积分出来的一定是ln一定是放在分母，那么lnx此时没有积分符号，其值就是整体->0收敛，a<1时整体->∞发散