算法奇妙屋(八)-泰波那契数列模型

⚙️个人专栏:
《Java算法时空: 图解手撕原理》 《多线程》 《JavaSE基础原理》 《数据结构》
✨与其内耗自己,不如责备他人



目录
一. 力扣 1137. 第 N 个泰波那契数
1. 题目
2. 算法原理
(1) 动态规划常见步骤
(2) 空间优化
3. 代码
(1) 未优化的常规代码
(2) 空间优化后的代码
二. 力扣 面试题 08.01. 三步问题
1. 题目
2. 算法原理
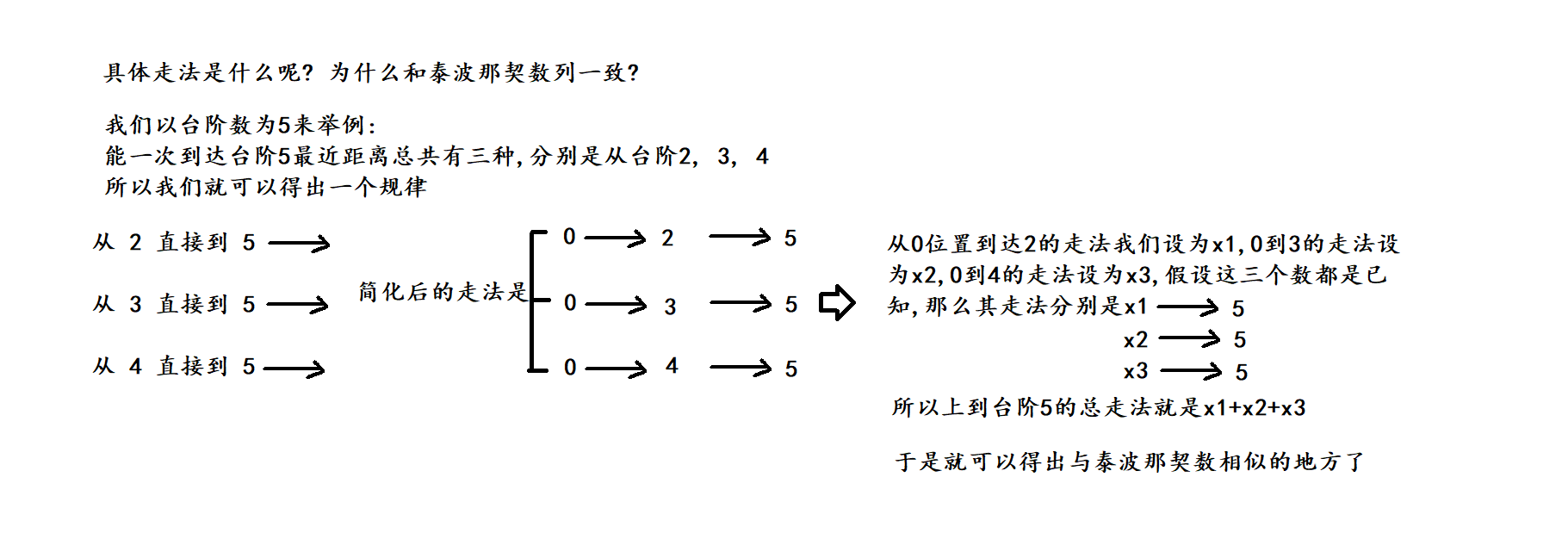
(1) 为什么说和泰波那契数列相似呢?
(2) 动态规划过程
3. 代码
三. 力扣 746. 使用最小花费爬楼梯
1. 题目
2. 算法原理
(1) 解法一:dp表以i为结尾
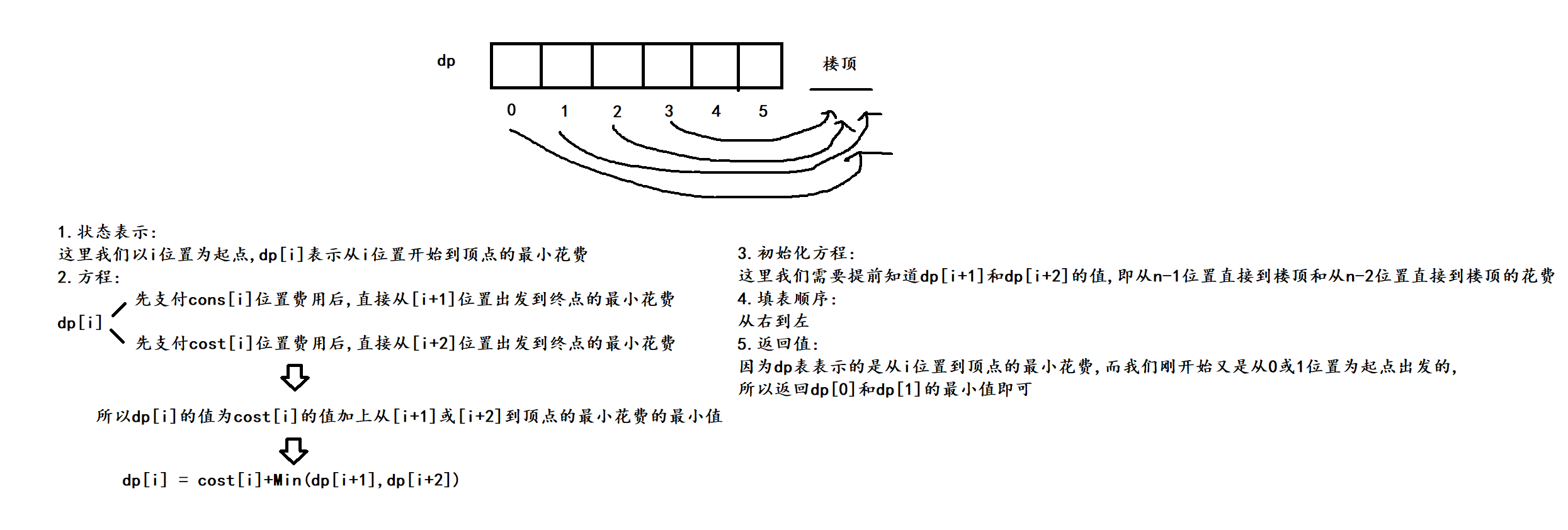
(2) 解法二:dp表以i位置为起点
3. 代码
(1) 解法一代码:
(2) 解法二代码:
一. 力扣 1137. 第 N 个泰波那契数
1. 题目

2. 算法原理
(1) 动态规划常见步骤
这里我们用的是动态规划思想, 具体请看图解
(2) 空间优化
3. 代码
(1) 未优化的常规代码
public int tribonacci(int n) {if (n == 0) {return 0;}if (n == 1 || n == 2) {return 1;}int[] dp = new int[n + 1];dp[0] = 0;dp[1] = dp[2] = 1;for (int i = 3; i < dp.length; i++) {dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];}return dp[n];}(2) 空间优化后的代码
public int tribonacci(int n) {if (n == 0) {return 0;}if (n == 1 || n == 2) {return 1;}int a = 0;int b = 1, c = 1;int ret = 0;for (int i = 3; i <= n; i++) {ret = (a + b + c);a = b;b = c;c = ret;}return ret;}二. 力扣 面试题 08.01. 三步问题
1. 题目
题目很好理解, 即求上到n个台阶的总走法, 可以看出与泰波那契数列有点像
2. 算法原理
(1) 为什么说和泰波那契数列相似呢?
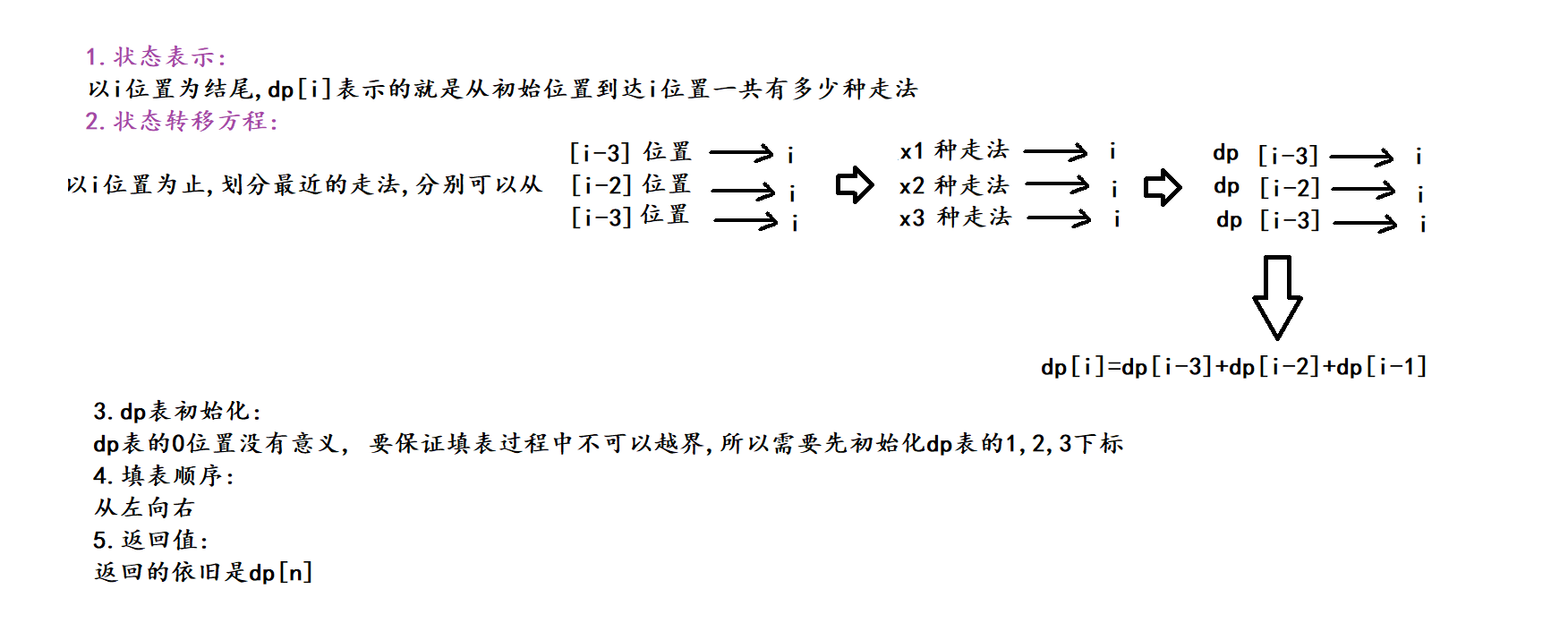
(2) 动态规划过程
3. 代码
public int waysToStep(int n) {if (n == 1 || n == 2) {return n;}if (n == 3) {return 4;}int MOD = (int) 1e9 + 7;int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;dp[3] = 4;for (int i = 4; i <= n; i++) {dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}return dp[n];}三. 力扣 746. 使用最小花费爬楼梯
1. 题目
1.
2.
2. 算法原理
(1) 解法一:dp表以i为结尾
(2) 解法二:dp表以i位置为起点
3. 代码
(1) 解法一代码:
public int minCostClimbingStairs(int[] cost) {int n = cost.length;int[] dp = new int[n + 1];for (int i = 2; i <= n; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);}return dp[n];}(2) 解法二代码:
public int minCostClimbingStairs(int[] cost) {int n = cost.length;int[] dp = new int[n];dp[n - 1] = cost[n - 1];dp[n - 2] = cost[n - 2];for (int i = n - 3; i >= 0; i--) {dp[i] = cost[i] + Math.min(dp[i + 1], dp[i + 2]);}return Math.min(dp[0],dp[1]);}