当前位置：首页 > news >正文

洛谷 P2437：蜜蜂路线 ← 高精度加法 + Fibonacci

news 来源：原创 2025/6/14 10:20:28

【题目来源】
https://www.luogu.com.cn/problem/P2437

【题目描述】
一只蜜蜂在下图所示的数字蜂房上爬动，已知它只能从标号小的蜂房爬到标号大的相邻蜂房，现在问你：蜜蜂从蜂房 m 开始爬到蜂房 n，m<n，有多少种爬行路线？

【输入格式】
输入 m，n 的值。

【输出格式】
爬行有多少种路线？

【输入样例】
1 14

【输出样例】
377

【说明/提示】
对于100%的数据，1≤M,N≤1000

【算法分析】
● 由题意可知，蜜蜂依蜂房 1 至蜂房 n 的顺序爬行。

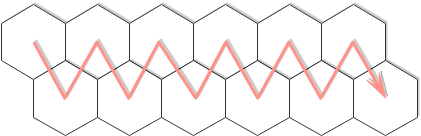
故蜜蜂要想爬到第 i 号蜂房，只能从第 i-1 号蜂房爬一步或从第 i-2 号蜂房爬两步而得。

所以，若设 f[i] 表示蜜蜂爬到第 i 号蜂房的路线数，则 f[i]=f[i-1]+f[i-2]。

● 蜜蜂从蜂房 m 开始爬到蜂房 n，m<n，经过 n-m+1 个蜂房。依据前述分析，相当于求斐波那契数列的第 n-m+1 项。

● 高精度加法：https://blog.csdn.net/hnjzsyjyj/article/details/144656955
易看出，路线数 f[i]=f[i-1]+f[i-2] 为斐波那契数列。由于 long long 最大能表示到斐波那契数列的第 92 项，其值为 7,540,113,804,746,346,429。而本题可取到第 1000 项，因此需要使用高精度加法。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

const int maxn=5e3+5;
string s[maxn];

string hiAdd(string a,string b) {
    string c;
    int t=0;
    int i=a.size()-1,j=b.size()-1;
    while(i>=0 || j>=0) {
        if(i>=0) t+=(a[i]-'0');
        if(j>=0) t+=(b[j]-'0');
        c+=(t%10+'0');
        t/=10;
        i--,j--;
    }
    if(t!=0) c+=(t+'0');
    reverse(c.begin(),c.end());
    return c;
}

int main() {
    int m,n;
    cin>>m>>n;
    
    s[1]=s[2]="1";
    for(int i=3; i<=n-m+1; i++) {
        s[i]=hiAdd(s[i-1],s[i-2]);
    }
    cout<<s[n-m+1];

    return 0;
}

/*
in:
1 14

out:
377
*/

【参考文献】
https://www.luogu.com.cn/problem/solution/P2437
https://www.cnblogs.com/IronMan-PZX/p/18132981