当前位置：首页 > news >正文

LoRA 微调大模型直观的理解

news 2025/10/18 11:29:18

LoRA 微调大模型直观的理解

flyfish

LoRA 的全称是 Low-Rank Adaptation（低秩适配），完整表述为 Low-Rank Adaptation of Large Language Models（大语言模型的低秩适配）

全连接网络可被描述为一系列加权连接：每个输入都会与某个权重相乘，随后所有结果相加，进而生成输出。

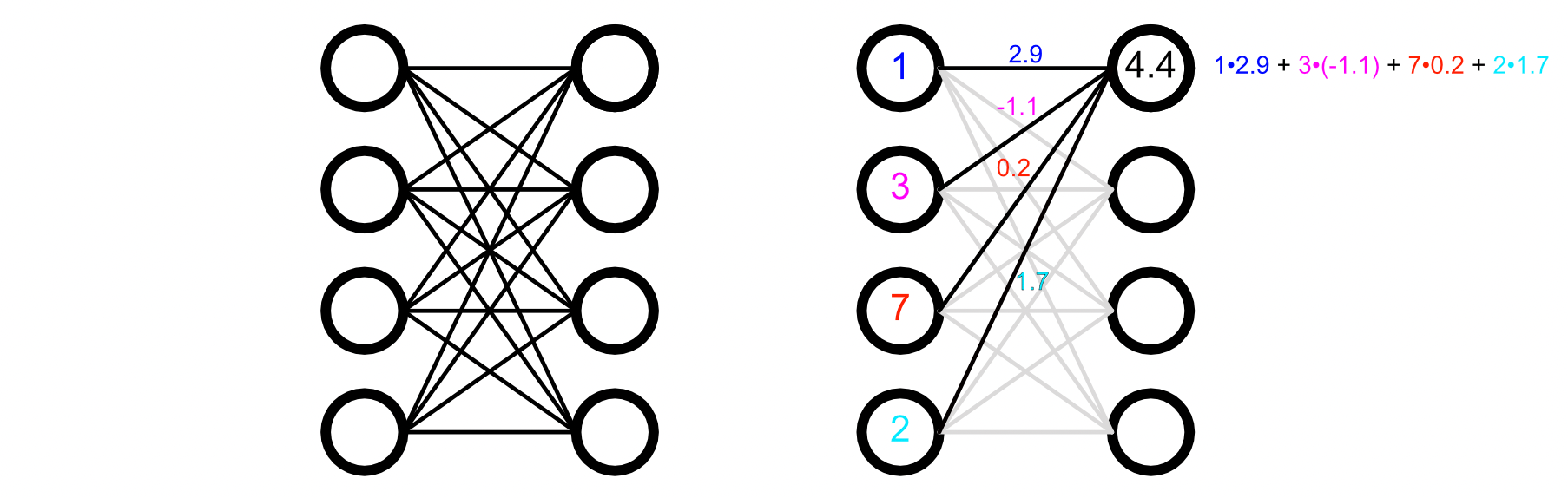
在这里插入图片描述
按照神经元列表的形式说

左侧有4个输入神经元，数值分别是 1、3、7、2；

它的计算过程是这样的：
每个输入都会通过一条带权重的连线连接到这个目标神经元，连线标注的权重分别是2.9、-1.1、0.2、1.7。

按照“输入×对应权重，再求和”的规则：

第一个输入（1）×对应权重（2.9）： $1 \times 2.9 = 2.9$
第二个输入（3）×对应权重（-1.1）： $3 \times (- 1.1) = - 3.3$
第三个输入（7）×对应权重（0.2）： $7 \times 0.2 = 1.4$
第四个输入（2）×对应权重（1.7）： $2 \times 1.7 = 3.4$

最后把这些乘积加起来： $2.9 + (- 3.3) + 1.4 + 3.4 = 4.4$
即某个特定神经元的数值，等于所有输入分别与其对应权重相乘后的总和。
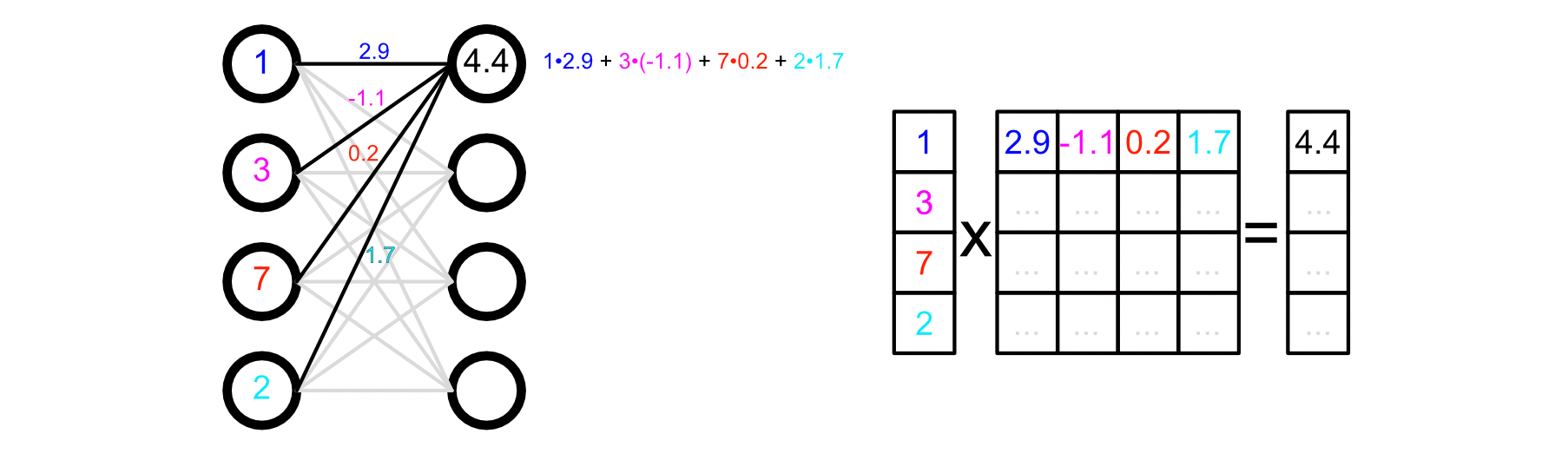
在这里插入图片描述
全连接网络的左侧理解为加权连接，其底层运算通过矩阵乘法实现，即右侧矩阵乘法。在右侧的图表中，左侧的向量是输入，中间的矩阵是权重矩阵，右侧的向量是输出。

矩阵的秩

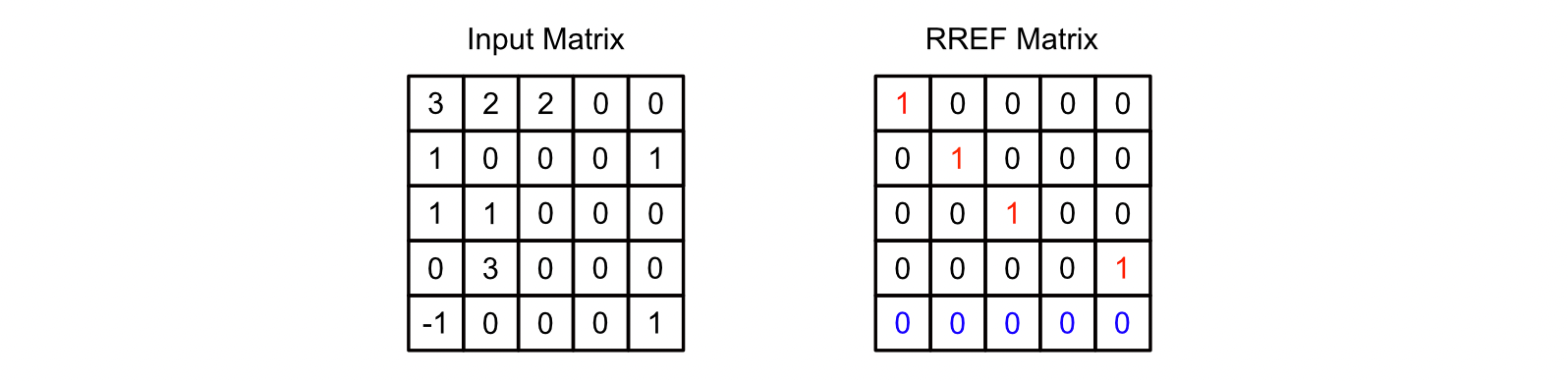
在这里插入图片描述
行最简形（RREF）：reduced row echelon form

左侧是一个矩阵，右侧是该矩阵转化为行最简形（RREF）后的矩阵。在行最简形矩阵中，能看到有四个线性无关的向量（行）——这些向量里的每一个，都可以通过组合来描述输入矩阵中的所有向量。

通过把矩阵分解成这种形式，能数出有多少个“线性无关的向量”可以用来描述原始矩阵。而线性无关向量的数量，就是矩阵的“秩”。上面这个行最简形矩阵的秩为4，因为存在四个线性无关的向量。

无论从“行向量”的角度，还是从“列向量”的角度去分析一个矩阵，它的秩始终是相同的。

矩阵分解

矩阵会以线性相关的形式包含一定程度的 “重复信息”。我们可以利用「分解」的思路，用两个更小的矩阵来表示一个大矩阵 —— 就像一个大数字能表示为两个更小数字的乘积一样，一个矩阵也能看作是两个更小矩阵的乘积。
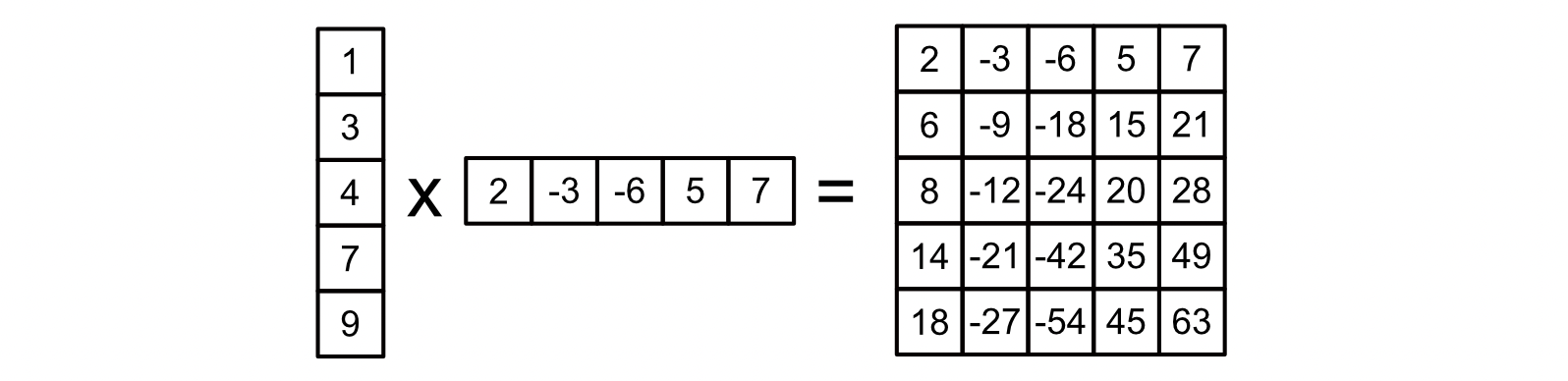
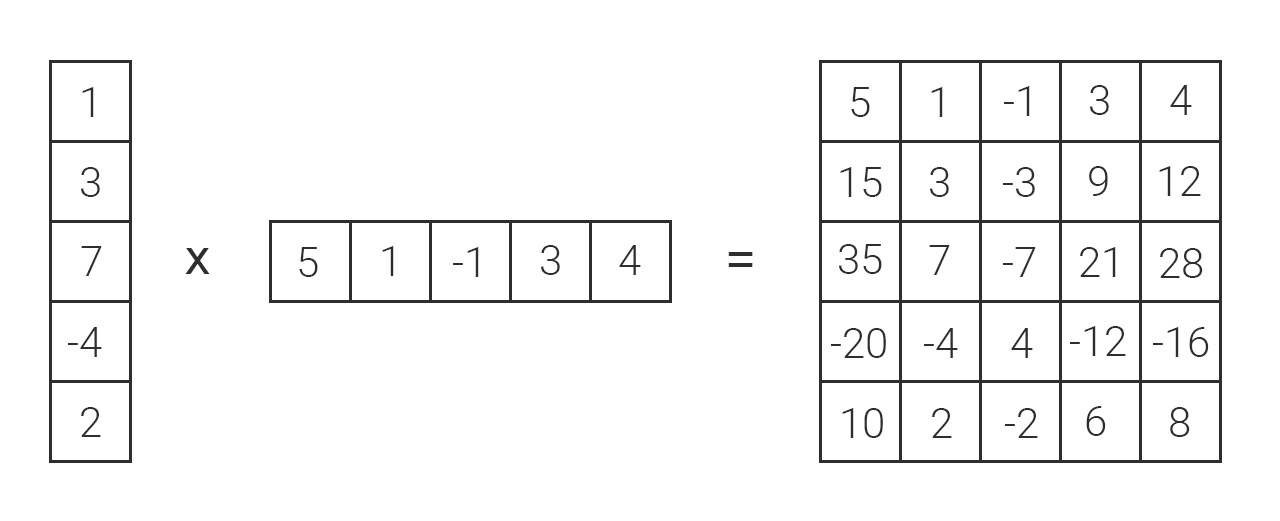
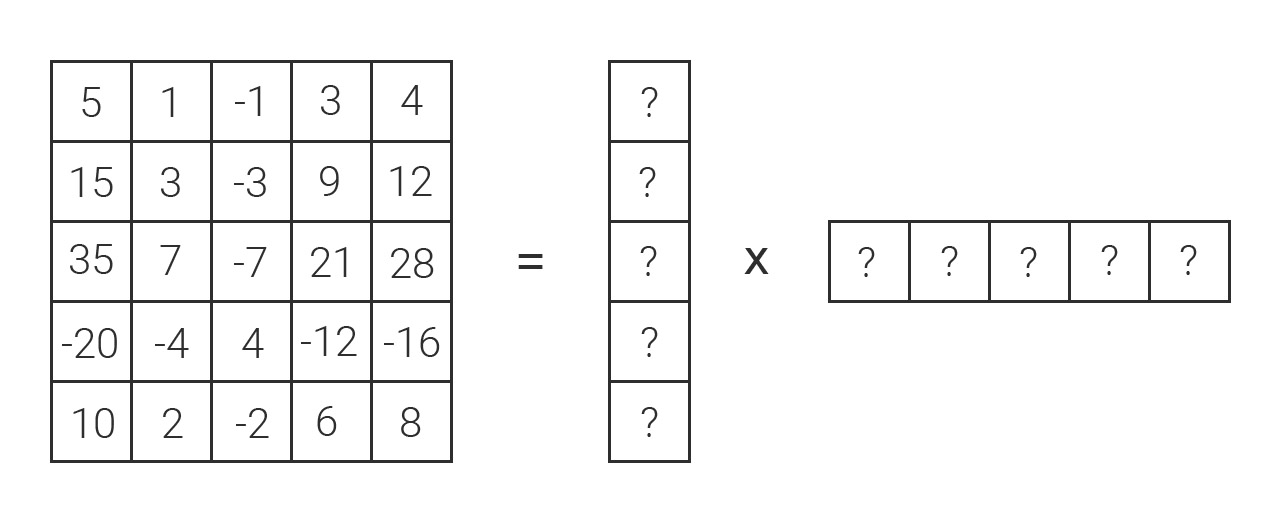
在这里插入图片描述

左侧的列向量与行向量相乘后，结果与右侧的大矩阵完全等价。尽管二者表达的数值是一致的，但左侧两个向量占用的存储空间只有右侧矩阵的 40%。而且，矩阵的规模越大，这种 “用小矩阵（因子）表示大矩阵” 的方式，就越能显著节省空间。
如果有一个大矩阵，且它的线性相关程度很高（因此秩很低），就可以把这个矩阵表示为两个相对小的矩阵的乘积。这种 “矩阵分解” 的思路，正是 LoRA 能占用如此小内存的原因。
在这里插入图片描述

在这里插入图片描述

例子

秩1矩阵的分解
假设有一个 $\times 3$ 的矩阵 $A$ ：
$\begin{pmatrix} 2 & 4 & 6 \\ -1 & -2 & -3 \\ 3 & 6 & 9 \end{pmatrix}$

1. 分析“线性相关”与“秩低”

观察矩阵 $A$ 的行：

第二行 $(- 1, - 2, - 3)$ 是第一行的 $−12-\frac{1}{2}$ 倍（ $\times (-\frac{1}{2}) = -1$ ， $\times (-\frac{1}{2}) = -2$ ， $\times (-\frac{1}{2}) = -3$ ）；
第三行 $(3, 6, 9)$ 是第一行的 $32\frac{3}{2}$ 倍（ $\times \frac{3}{2} = 3$ ， $\times \frac{3}{2} = 6$ ， $\times \frac{3}{2} = 9$ ）。

这说明：矩阵 $A$ 的行向量线性相关性极强（所有行都能由“第一行”通过“缩放”得到），因此它的秩为1（只有1个“线性无关”的行向量）。

2. 分解为两个小矩阵（向量）的乘积

根据线性代数中“秩1矩阵可表示为两个向量的外积”的性质，我们可以把 $A$ 拆成：

一个列向量 $u\mathbf{u}$ （存储“每行的缩放系数”）；
一个行向量 $vT\mathbf{v}^T$ （存储“基础行向量”）。

具体来说：

列向量 $u=(1−1232)\mathbf{u} = \begin{pmatrix} 1 \\ -\frac{1}{2} \\ \frac{3}{2} \end{pmatrix}$ （第一行系数为1，第二行系数为 $−12-\frac{1}{2}$ ，第三行系数为 $32\frac{3}{2}$ ）；
行向量 $vT=(246)\mathbf{v}^T = \begin{pmatrix} 2 & 4 & 6 \end{pmatrix}$ （取第一行作为“基础向量”）。

此时，矩阵 $A$ 等于这两个向量的乘积：
$u×vT=(1−1232)×(246)=(1×21×41×6−12×2−12×4−12×632×232×432×6)=(246−1−2−3369)=A\mathbf{u} \times \mathbf{v}^T = \begin{pmatrix} 1 \\ -\frac{1}{2} \\ \frac{3}{2} \end{pmatrix} \times \begin{pmatrix} 2 & 4 & 6 \end{pmatrix} = \begin{pmatrix} 1 \times 2 & 1 \times 4 & 1 \times 6 \\ -\frac{1}{2} \times 2 & -\frac{1}{2} \times 4 & -\frac{1}{2} \times 6 \\ \frac{3}{2} \times 2 & \frac{3}{2} \times 4 & \frac{3}{2} \times 6 \end{pmatrix} = \begin{pmatrix} 2 & 4 & 6 \\ -1 & -2 & -3 \\ 3 & 6 & 9 \end{pmatrix} = A$

3. 验证“压缩效果”

原始矩阵 $A$ 是 $\times 3$ ，需要存储 $\times 3 = 9$ 个元素；
分解后的两个向量：列向量 $u\mathbf{u}$ （ $\times 1$ ，存3个元素） + 行向量 $vT\mathbf{v}^T$ （ $\times 3$ ，存3个元素），总共只需存 $3 + 3 = 6$ 个元素。

不同的分解方式

1. 第一种分解

取列向量 $u=(1−1232)\mathbf{u} = \begin{pmatrix} 1 \\ -\frac{1}{2} \\ \frac{3}{2} \end{pmatrix}$ ，行向量 $vT=(246)\mathbf{v}^T = \begin{pmatrix} 2 & 4 & 6 \end{pmatrix}$ ，则：
$u×vT=(1−1232)×(246)=A\mathbf{u} \times \mathbf{v}^T = \begin{pmatrix} 1 \\ -\frac{1}{2} \\ \frac{3}{2} \end{pmatrix} \times \begin{pmatrix} 2 & 4 & 6 \end{pmatrix} = A$

2. 第二种分解

取列向量 $u′=(2−13)\mathbf{u}' = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}$ ，行向量 $v′T=(123)\mathbf{v}'^T = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix}$ ，则：
$u′×v′T=(2−13)×(123)=(2×12×22×3−1×1−1×2−1×33×13×23×3)=A\mathbf{u}' \times \mathbf{v}'^T = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \times \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} = \begin{pmatrix} 2×1 & 2×2 & 2×3 \\ -1×1 & -1×2 & -1×3 \\ 3×1 & 3×2 & 3×3 \end{pmatrix} = A$

LoRA（Low-Rank Adaptation）微调的直觉理解

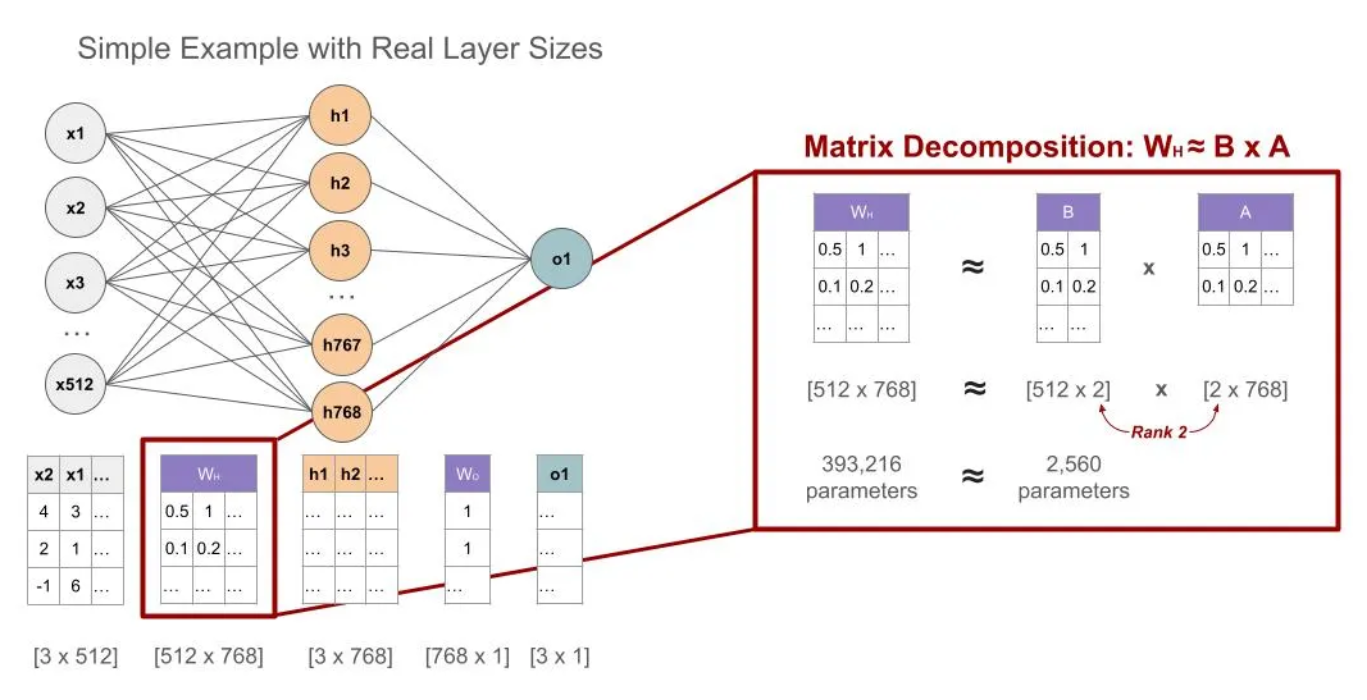
在这里插入图片描述

1. 网络结构概述

输入层：包含512个输入特征（如 $x 1, x 2, ..., x 512$ ），维度为 $\times 512]$ （3个样本，每个512维）。
隐藏层：包含768个神经元（如 $h 1, h 2, ..., h 768$ ），维度为 $\times 768]$ 。
输出层：1个输出单元（如 $o 1$ ），维度为 $\times 1]$ 。
权重矩阵：
$Wh∈R512×768W_h \in \mathbb{R}^{512 \times 768}$ ：从输入到隐藏层的权重矩阵。
$Wo∈R768×1W_o \in \mathbb{R}^{768 \times 1}$ ：从隐藏层到输出层的权重矩阵。

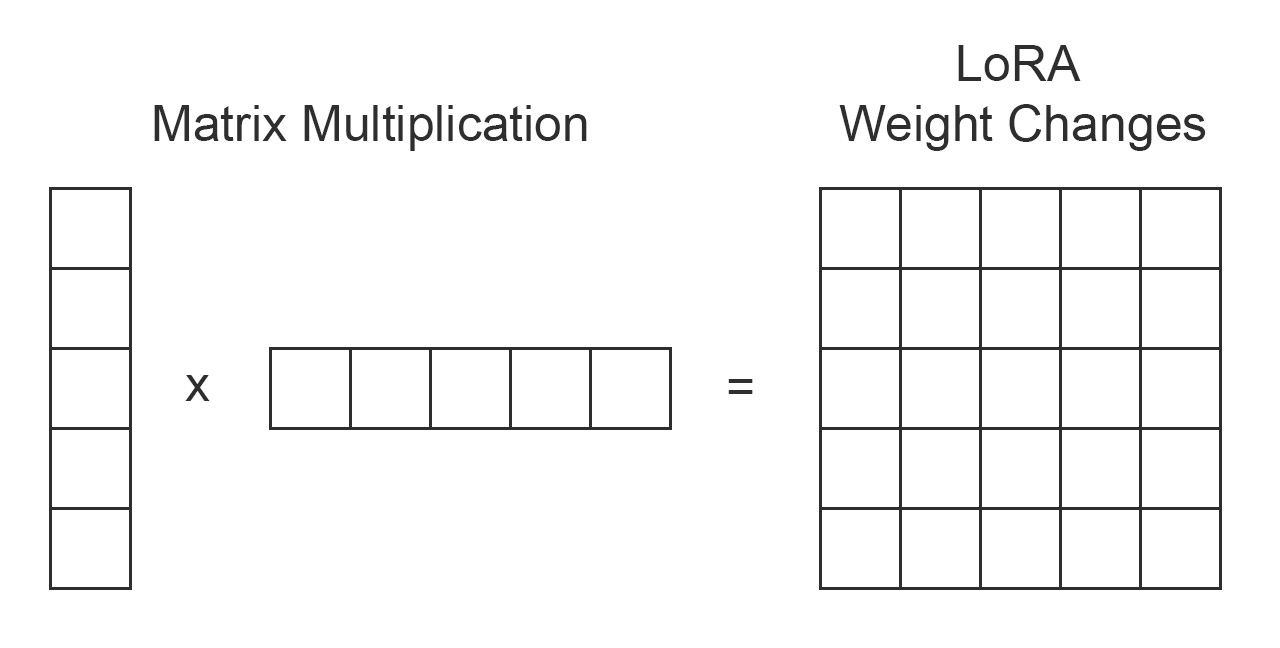
2. LoRA的思想

LoRA通过低秩分解对权重矩阵 $W_h$ 进行高效更新，而不是直接修改其所有参数。

$Wh≈B×AW_h \approx B \times A$
$W_h$ 的原始维度是 $512 \times 768]$ ，包含393,216个参数。
通过LoRA分解为两个小矩阵的乘积：
$\in \mathbb{R}^{512 \times r}$
$\in \mathbb{R}^{r \times 768}$
其中 $r$ 是秩，这里指定为2。

3. 矩阵分解细节

分解形式： $Wh≈B×AW_h \approx B \times A$
$B$ （部分）：
$\begin{bmatrix} 0.5 & 1 \\ 0.1 & 0.2 \\ \vdots & \vdots \end{bmatrix} \in \mathbb{R}^{512 \times 2}$
$A$ （部分）：
$\begin{bmatrix} 0.5 & 1 & \cdots \\ 0.1 & 0.2 & \cdots \end{bmatrix} \in \mathbb{R}^{2 \times 768}$
乘积 $\times A$ 近似还原 $W_h$ 的更新部分 $ΔW\Delta W$ ，维度仍为 $512 \times 768]$ 。
参数量计算：
原始 $W_h$ ： $512 \times 768 = 393,216$ 个参数。
LoRA新增参数： $512 \times 2) + (2 \times 768) = 1,024 + 1,536 = 2,560$ 个参数。
这种分解将参数量从393,216减少到2,560

简单说就是

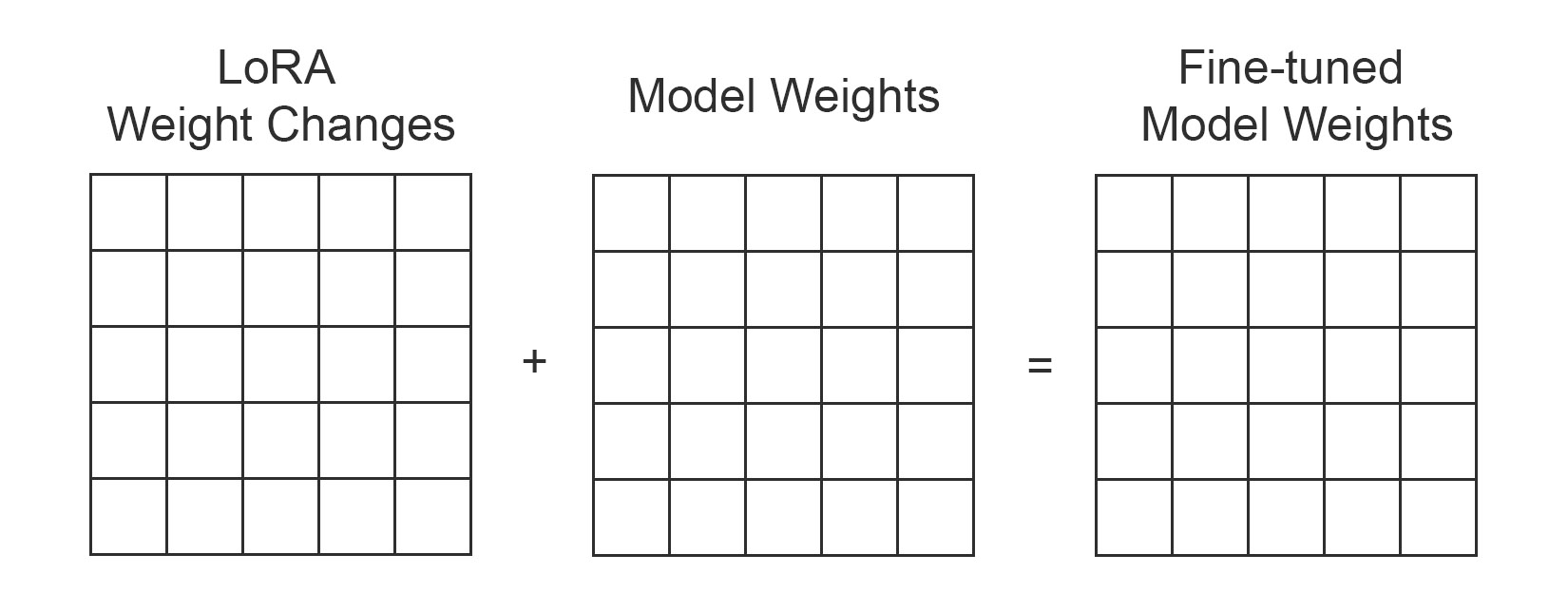
对于权重矩阵 $W_h$ ，LoRA假设其更新可以表示为低秩形式 $ΔWh=B×A\Delta W_h = B \times A$ 。
原矩阵 $W_h$ 冻结，新增矩阵A和B进行训练。
最终输出为 $W_h \cdot x + \Delta W_h \cdot x = (W_h + B \cdot A) \cdot x$ 。

稍微严谨的话说就是
对于神经网络中的权重矩阵 $\in \mathbb{R}^{d \times k}$ （例如从输入层到隐藏层的线性变换），LoRA假设其任务特定的更新 $ΔW\Delta W$ 可以分解为两个低秩矩阵 $\in \mathbb{R}^{d \times r}$ 和 $\in \mathbb{R}^{r \times k}$ 的乘积，其中 $r$ 是秩，远小于 $min⁡(d,k)\min(d, k)$ 。因此：

原有前向传播： $\cdot x$
LoRA调整后： $\Delta W) \cdot x = (W + B \cdot A) \cdot x$

这里：

$W$ 是冻结的预训练权重，不更新。
$ΔW=B⋅A\Delta W = B \cdot A$ 是新增的可训练参数，秩为 $r$ 。

通常会看到这样的表达 $rank≪min⁡(m,n)\text{rank} \ll \min(m, n)$

$rank\text{rank}$ ：表示矩阵的秩，它是矩阵中“线性无关的行向量（或列向量）的最大数量”，反映矩阵包含的“独立信息维度”。
$≪\ll$ ：是数学中表示“远小于”的符号，用于强调前者的数值比后者小很多（非正式但广泛使用的约定符号）。
$min⁡(m,n)\min(m, n)$ ： $min⁡\min$ 是“取最小值”的函数； $m$ 和 $n$ 通常代表矩阵的行数和列数（比如一个 $\times n$ 的矩阵，有 $m$ 行、 $n$ 列）。因此 $min⁡(m,n)\min(m, n)$ 的意思是“取行数 $m$ 和列数 $n$ 中较小的那个值”。