当前位置：首页 > news >正文

2025年--Lc196-712. 两个字符串的最小ASCII删除和（动态规划在字符串的应用）--Java版

news 2025/10/18 11:27:47

1.题目

在这里插入图片描述

2.思路

（1）在下标为[1, m - 1]的字符串s1 = “ea” 与下标为[0, n - 1]的字符串s2 = "eat"中寻找相等的字符串。
定义dp数组，多开一行一列存储空字符串
s1 前 i 个字符 (s1[0…i-1])和 s2 前 j 个字符 (s2[0…j-1])，能匹配（不删除）的字符的 ASCII 总和的最大值。
sum存的是两个字符串的ascii码值
（2）初始化第一行第一列默认是0
（3）遍历顺序，从第二行第二列开始遍历

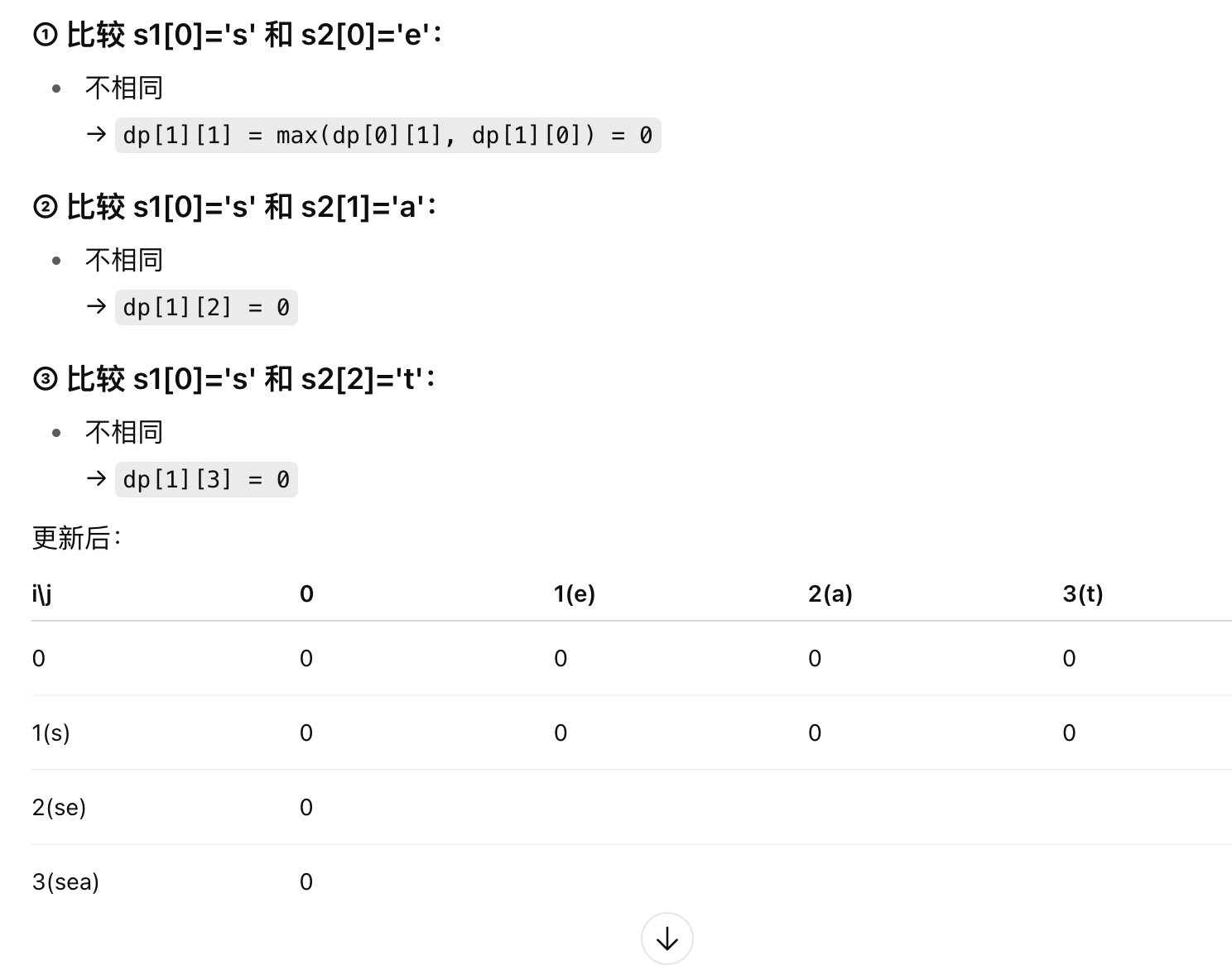
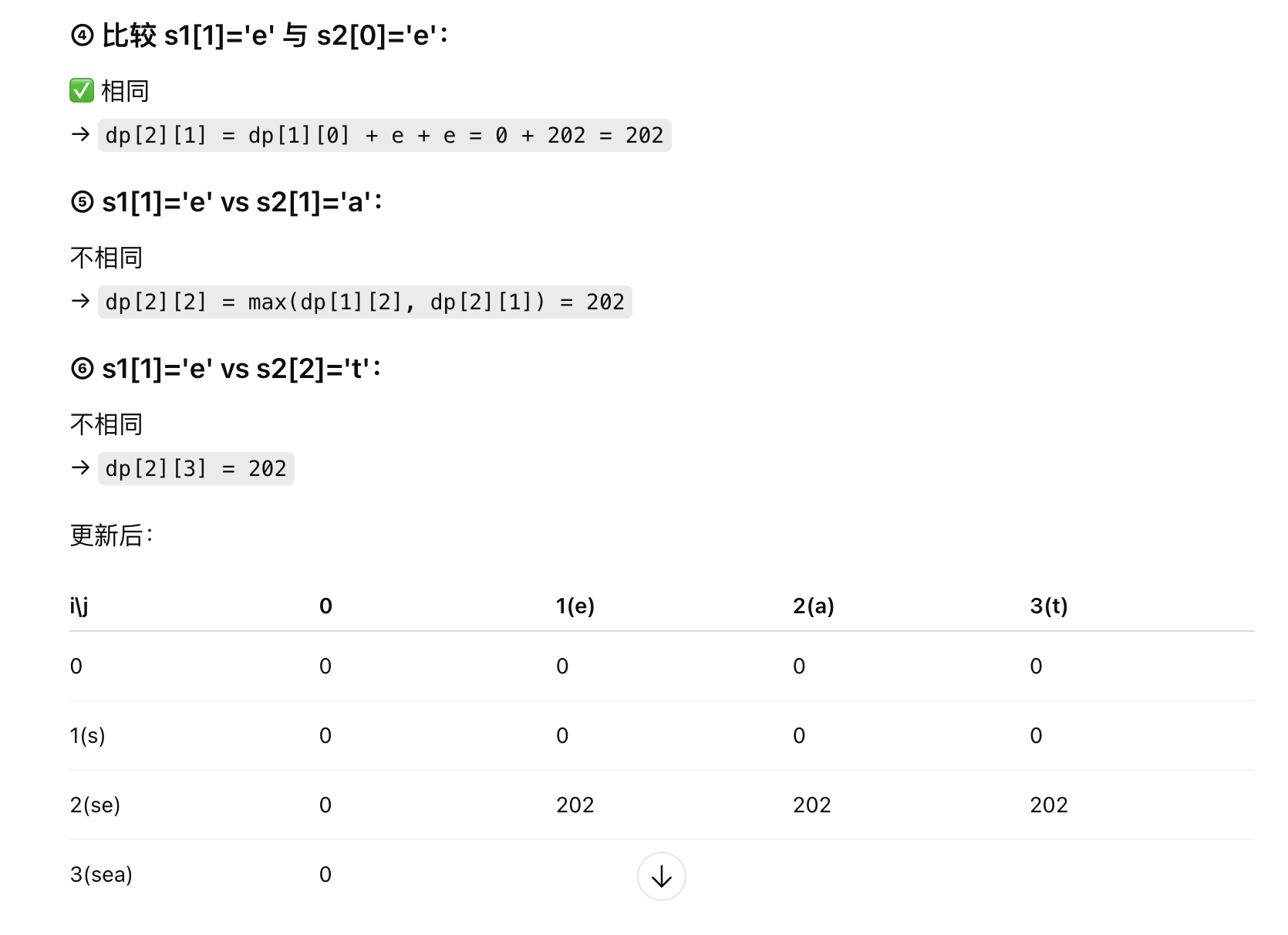
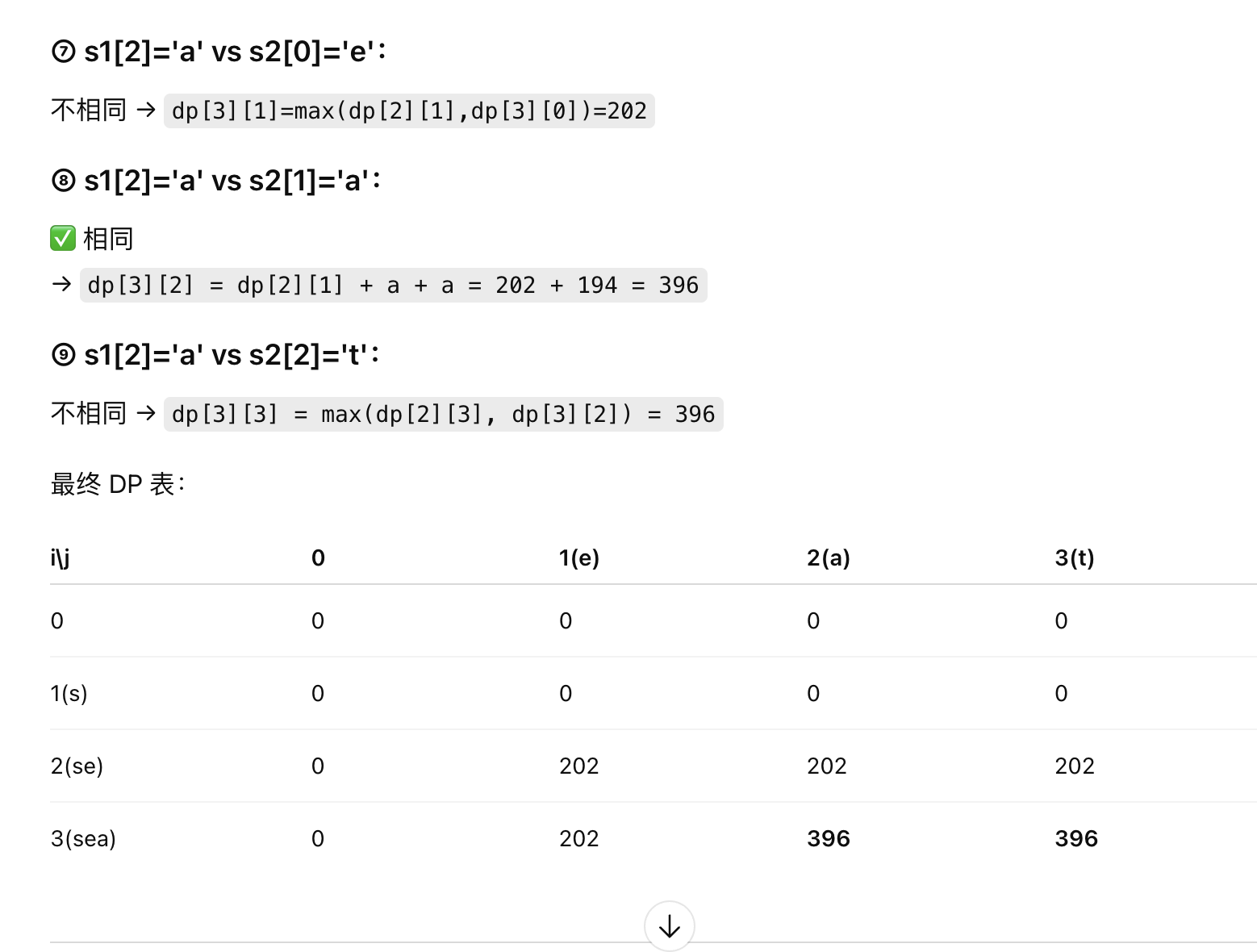
在这里插入图片描述

3.代码实现

class Solution {public int minimumDeleteSum(String s1, String s2) {int m=s1.length();int n=s2.length();int sum=0;//定义dp数组，多开一行一列存储空字符串//s1 前 i 个字符 (s1[0..i-1])和 s2 前 j 个字符 (s2[0..j-1])，能匹配（不删除）的字符的 ASCII 总和的最大值。int[][] dp=new int[m+1][n+1];//把字符串变成字符数组for(char ch:s1.toCharArray())sum=sum+ch;for(char ch:s2.toCharArray())sum=sum+ch;//默认第一行第一列都为0，因为空字符串，最小的ascii码for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){char a=s1.charAt(i-1);char b=s2.charAt(j-1);if(a==b)//“保留这对相同字符”，那么能匹配的 ASCII 总和就等于“前面匹配的 + 这两个字符的值”。{dp[i][j]=dp[i-1][j-1]+a+b;}else//字符不相同，要让删除的和最小，所以现在就要让匹配的字符的ASCII码的和最大{dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}}// sum 是两串所有字符之和；dp[m][n] 是“保留的公共部分”的双倍和return sum-dp[m][n];}
}