当前位置：首页 > news >正文

从零掌握贪心算法Java版：LeetCode 10题实战解析（上）

news 2025/10/18 11:23:12

1.前言

插播一条消息~

2正文

2.1概念讲解

2.2.题目奉上

2.2.1柠檬水找零

2.2.2将数组和减半的最少操作次数

2.2.3最大数

2.2.4摆动序列

2.2.5最长递增子序列

2.2.6递增的三元子序列

2.2.7最长连续递增序列

2.2.8买卖股票的最佳时机

2.2.9买卖股票的最佳时机 II

2.2.10K次取反后最大化的数组和

3.小结

1.前言

在算法世界里，有一种思想如同生活中的"见好就收"——每次做出当前看来最优的选择，寄希望于通过局部最优达成全局最优。这种思想就是贪心算法，它以其简洁高效的特点，成为解决最优问题的利器。今天我们就来系统学习贪心算法的核心思想，并通过10道LeetCode经典题目实战演练，带你掌握这种"步步为营"的解题思维。

插播一条消息~

🔍十年经验淬炼 · 系统化AI学习平台推荐

系统化学习AI平台https://www.captainbed.cn/scy/

📚 完整知识体系：从数学基础 → 工业级项目（人脸识别/自动驾驶/GANs），内容由浅入深
💻 实战为王：每小节配套可运行代码案例（提供完整源码）
🎯 零基础友好：用生活案例讲解算法，无需担心数学/编程基础

🚀 特别适合

想系统补强AI知识的开发者
转型人工智能领域的从业者
需要项目经验的学生

2正文

2.1概念讲解

什么是贪心算法？

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。它的核心思想可以概括为：局部最优策略，逐步逼近全局最优。

举个生活中的例子：如果你要从家里出发去公司，贪心策略就是每次选择眼前最近的路口前进，而不考虑长远路线；而动态规划则会规划所有可能路线后选择最优解。

贪心算法的基本要素

实现贪心算法需要满足两个关键条件：

贪心选择性质：所求问题的整体最优解可以通过一系列局部最优的选择来达到
最优子结构性质：问题的最优解包含子问题的最优解

贪心与动态规划的对比

特性	贪心算法	动态规划
决策方式	自顶向下，每次做局部最优选择	自底向上，存储子问题解
子问题关系	独立无关联	重叠且依赖
适用场景	有明显贪心选择性质的问题	多阶段决策问题
时间复杂度	通常为O(n)或O(nlogn)	通常为O(n²)或O(n³)
空间复杂度	通常为O(1)或O(n)	通常为O(n)或O(n²)

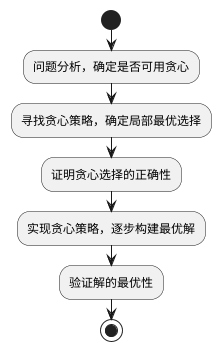
贪心算法的一般流程

2.2.题目奉上

2.2.1柠檬水找零

问题描述：在柠檬水摊上，每一杯柠檬水的售价为5美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付5美元。一开始你手头没有任何零钱。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

贪心策略：优先使用大额钞票找零，保留更多小额钞票以应对未来可能的找零需求。

代码解析：

public boolean lemonadeChange(int[] bills) {int five = 0, ten = 0, twenty = 0; // 记录三种钞票的数量int n = bills.length;for(int i = 0; i < n; i++){if(bills[i] == 5){// 收5美元，不用找零，直接增加5美元钞票数量five++;}else if(bills[i] == 10){// 收10美元，需要找5美元ten++;if(five < 1){ // 如果没有5美元钞票，无法找零return false;}five--; // 用一张5美元找零}else{// 收20美元，有两种找零方式：1张10+1张5，或3张5twenty++;if(ten > 0 && five > 0){ // 优先使用10+5的组合，保留更多5美元five--;ten--;}else if(five > 2){ // 其次使用3张5美元five -= 3;} else{ // 两种方式都无法找零return false;}}}return true; // 所有顾客都能正确找零
}

关键思路：20美元找零时，优先消耗10美元钞票，因为5美元钞票在后续找零中更灵活。这就像生活中我们钱包里如果有小面额钞票，会尽量先用大面额付款，保留小面额以备不时之需。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)，其中n为顾客数量。

2.2.2将数组和减半的最少操作次数

问题描述：给你一个正整数数组 nums 。每一次操作中，你可以选择 nums 中任意一个元素并将它减小到恰好一半。（注意，在后续操作中你可以对减半过的元素继续执行操作）。请你返回将数组和至少减少一半的最少操作数。

贪心策略：每次选择当前数组中最大的元素进行减半，这样可以最快地减少数组总和。

代码解析：

public int halveArray(int[] nums) {// 使用大根堆（优先级队列）存储数组元素，默认是小根堆，通过比较器实现大根堆PriorityQueue<Double> pq = new PriorityQueue<>((a, b) -> b.compareTo(a));double sum = 0.0; // 数组总和// 初始化大根堆并计算总和for (int num : nums) {pq.offer((double) num);sum += num;}sum /= 2.0; // 需要减少到的目标总和（原总和的一半）int ans = 0; // 操作次数// 每次取出最大元素减半，直到总和减少至少一半while (sum > 0.0) {double max = pq.poll() / 2.0; // 取出最大元素并减半sum -= max; // 总和减少max（因为我们将元素减少了max）pq.offer(max); // 将减半后的元素放回堆中ans++; // 操作次数加1}return ans;
}

生活类比：这就像我们有一堆不同大小的石头，要最快地将石头总量减少一半，每次肯定会先搬最大的那块石头。

复杂度分析：时间复杂度O(nlogn)，其中n为数组长度，每次堆操作需要O(logn)时间；空间复杂度O(n)，用于存储堆。

2.2.3最大数

问题描述：给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

贪心策略：自定义排序规则，对于两个数字a和b，比较ab和ba哪个组合更大，从而决定它们的排列顺序。

代码解析：

public String largestNumber(int[] nums) {// 将整数数组转换为字符串数组String[] strs = new String[nums.length];for(int i = 0; i < nums.length; i++){strs[i] = nums[i] + "";}// 自定义排序规则：比较b+a和a+b的大小Arrays.sort(strs, (a, b) -> (b + a).compareTo(a + b));// 拼接排序后的字符串StringBuilder sb = new StringBuilder();for(String str : strs){sb.append(str);}// 特殊情况处理：如果结果以0开头，说明所有数字都是0if(sb.charAt(0) == '0'){return "0";}return sb.toString();
}

关键思路：排序规则是本题的核心。例如比较3和30：330 vs 303，显然330更大，所以3应该排在30前面。这种局部最优的比较最终会得到全局最优的结果。

复杂度分析：时间复杂度O(nlogn)，主要是排序操作；空间复杂度O(n)，用于存储字符串数组。

2.2.4摆动序列

问题描述：如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。给定一个整数序列，返回作为摆动序列的最长子序列的长度。

贪心策略：记录序列中的上升和下降趋势变化，每当趋势发生变化时，增加摆动序列长度。

代码解析：

public int wiggleMaxLength(int[] nums) {int n = nums.length;if(n < 2) return n; // 少于两个元素的序列是摆动序列int ans = 0; // 摆动次数int left = 0; // 前一个差值for(int i = 0; i < n - 1; i++){int right = nums[i + 1] - nums[i]; // 当前差值if(right == 0) continue; // 差值为0，不影响摆动序列// 如果当前差值与前一个差值异号（或前一个差值为0），说明发生了摆动if(left * right <= 0){ans++;left = right; // 更新前一个差值}}return ans + 1; // 摆动次数+1就是序列长度
}

示例分析：以序列[1,7,4,9,2,5]为例，差值序列为[6,-3,5,-7,3]，摆动发生在6→-3、-3→5、5→-7、-7→3，共4次摆动，所以序列长度为5。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)。

2.2.5最长递增子序列

问题描述：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

贪心策略：维护一个递增序列，对于每个新元素，若大于序列最后一个元素则加入，否则替换序列中第一个大于等于它的元素，这样可以为后续元素留出更多空间。

代码解析：

public int lengthOfLIS(int[] nums) {ArrayList<Integer> list = new ArrayList<>();int n = nums.length;list.add(nums[0]); // 初始化序列for (int i = 1; i < n; i++) {if(nums[i] > list.get(list.size() - 1)){// 当前元素大于序列最后一个元素，直接加入list.add(nums[i]);}else {// 二分查找找到第一个大于等于nums[i]的元素位置int left = 0, right = list.size() - 1;while (left < right) {int mid = (left + right) / 2;if(list.get(mid) < nums[i]){left = mid + 1;}else {right = mid;}}// 替换该位置的元素list.set(left, nums[i]);}}return list.size();
}

生活类比：这就像我们在玩俄罗斯方块，当新方块无法放在当前列时，我们会找到最合适的列放置，以留出更多空间给后续方块。

复杂度分析：时间复杂度O(nlogn)，其中n为数组长度，二分查找需要O(logn)时间；空间复杂度O(n)，用于存储序列。

2.2.6递增的三元子序列

问题描述：给你一个整数数组 nums ，判断这个数组中是否存在长度为 3 的递增子序列。

贪心策略：维护两个变量a和b，分别表示递增子序列的第一个和第二个元素，不断更新这两个值，使其尽可能小，为第三个元素的出现创造条件。

代码解析：

public boolean increasingTriplet(int[] nums) {if(nums.length < 3) return false; // 数组长度小于3，直接返回falseint a = nums[0], b = Integer.MAX_VALUE; // a为第一个元素，b为第二个元素for(int i = 1; i < nums.length; i++){if(nums[i] > b){// 找到第三个元素，返回truereturn true;}else if(nums[i] > a){// 更新b为更小的值，为后续元素留出空间b = nums[i];}else{// 更新a为更小的值a = nums[i];}}return false;
}

关键思路：这个算法的巧妙之处在于，a和b并不一定是最终三元组的前两个元素，但它们的存在表明已经有一个长度为2的递增序列，且我们在不断优化这个序列，使其更容易找到第三个元素。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)。

2.2.7最长连续递增序列

问题描述：给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

贪心策略：遍历数组，记录当前连续递增序列的起始位置，当序列不再递增时，更新起始位置并计算当前序列长度。

代码解析：

public int findLengthOfLCIS(int[] nums) {int n = nums.length;if (n == 1) return 1; // 数组长度为1，返回1int ans = 1; // 最长序列长度int left = 0; // 当前序列起始位置int right = 1; // 当前位置while(right < n) {if(nums[right] > nums[right - 1]) {// 连续递增，更新最长序列长度ans = Math.max(ans, right - left + 1);right++;} else {// 序列中断，更新起始位置left = right;right++;}}return ans;
}

示例分析：以数组[1,3,5,4,7]为例，连续递增序列有[1,3,5]（长度3）和[4,7]（长度2），所以最长为3。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)。

2.2.8买卖股票的最佳时机

问题描述：给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。

贪心策略：遍历数组，记录当前最低价格，计算每天卖出的利润，取最大值。

代码解析：

public int maxProfit(int[] prices) {int ans = 0; // 最大利润int minM = Integer.MAX_VALUE; // 最低价格for(int i = 0; i < prices.length; i++) {// 计算今天卖出的利润，并更新最大利润ans = Math.max(ans, prices[i] - minM);// 更新最低价格minM = Math.min(minM, prices[i]);}return ans;
}

生活类比：这就像我们炒股，每天都看看今天的价格和历史最低价相比能赚多少，同时记录新的最低价。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)。

2.2.9买卖股票的最佳时机 II

问题描述：给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

贪心策略：只要后一天价格高于前一天，就进行一次交易，赚取差价。

代码解析：

public int maxProfit(int[] prices) {int ans = 0; // 总利润// 遍历数组，只要后一天价格高于前一天，就进行交易for (int i = 0; i < prices.length - 1; i++) {if (prices[i] < prices[i + 1]) {ans += prices[i + 1] - prices[i];}}return ans;
}

示例分析：以 prices = [7,1,5,3,6,4] 为例，可进行的交易为(1→5)赚4，(3→6)赚3，总利润7。

复杂度分析：时间复杂度O(n)，空间复杂度O(1)。

2.2.10K次取反后最大化的数组和

问题描述：给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。重复这个过程恰好 k 次。可以多次选择同一个下标。以这种方式修改数组后，返回数组可能的最大和。

贪心策略：优先反转绝对值最大的负数，若没有负数则反转最小的正数（如果k为奇数）。

代码解析：

public int largestSumAfterKNegations(int[] nums, int k) {int ans = 0;int n = nums.length;// 计算初始总和for(int i = 0; i < n; i++) {ans += nums[i];}// 排序数组，便于找到绝对值最大的负数Arrays.sort(nums);// 优先反转绝对值最大的负数for(int i = 0; i < n; i++) {if(nums[i] < 0 && k > 0) {ans -= 2 * nums[i]; // 总和增加-2*nums[i]（因为nums[i]变为正数）nums[i] = -nums[i]; // 反转该数k--; // 剩余反转次数减1} else {break; // 遇到非负数，跳出循环}}// 如果还有剩余反转次数，且为奇数，反转最小的数if(k % 2 == 1) {// 重新排序找到最小的数Arrays.sort(nums);ans -= 2 * nums[0]; // 总和减少2*nums[0]（因为nums[0]变为负数）}return ans;
}

生活类比：这就像我们有一堆债务（负数）和资产（正数），要在有限的反转次数内最大化总资产，肯定会先把最大的债务转为资产，最后如果还有次数，就把最小的资产转为债务。

复杂度分析：时间复杂度O(nlogn)，主要是排序操作；空间复杂度O(1)（不考虑排序所需空间）。