网站查询空间商企业不开了网站备案吗
目录
- 1. 预备知识
- 1.1 低秩矩阵分解
- 2. 模拟举例
1. 预备知识
1.1 低秩矩阵分解
低秩矩阵分解是一种将高维矩阵近似为两个低维矩阵乘积的技术,常用于数据降维、压缩、推荐系统等领域。
步骤1:理解目标
我们有一个高维矩阵 ΔW\Delta WΔW ,希望将其近似为两个低维矩阵AAA和BBB的乘积,即ΔW≈BA\Delta W \approx BAΔW≈BA。
步骤2:设定矩阵维度
假设 ΔW\Delta WΔW是一个d×dd \times dd×d的矩阵。我们选择一个较小的整数 rrr,使得 r≪dr \ll dr≪d 。矩阵 AAA 的维度将是 d×rd \times rd×r ,矩阵 BBB 的维度将是 r×dr \times dr×d 。
步骤3:矩阵初始化
- 初始化矩阵 AAA 和 BBB 。可以使用随机初始化、正态分布初始化等方法。例如:
- A∼N(0,σ2)A \sim \mathcal{N}(0, \sigma^2)A∼N(0,σ2) ,表示矩阵 AAA 的每个元素都是从均值为0、方差为 σ2\sigma^2σ2 的正态分布中随机抽取的。
- BBB 初始化为零矩阵,即 B=0B = 0B=0 。
步骤4:矩阵乘积
-
通过矩阵乘积 BABABA ,可以得到一个近似的 d×dd \times dd×d 矩阵:
W’ = BA其中 W′≈ΔWW' \approx \Delta WW′≈ΔW 。
步骤5:优化和训练
- 在训练过程中,通过优化算法(如梯度下降),不断调整矩阵 AAA 和 BBB 的值,使得 W′W'W′ 更加接近于 ΔW\Delta WΔW 。
- 损失函数通常是衡量 ΔW\Delta WΔW 与 W′W'W′ 之间差距的一个函数,例如均方误差:
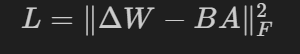
步骤6:更新规则
- 通过优化算法计算损失函数关于 AAA 和 BBB 的梯度,并更新 AAA 和 BBB 的值。例如,使用梯度下降法更新规则如下:
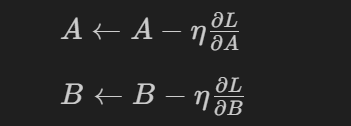
其中 η\etaη 是学习率。
2. 模拟举例
import numpy as np# 初始化矩阵 W
W = np.array([[4, 3, 2, 1],[2, 2, 2, 2],[1, 3, 4, 2],[0, 1, 2, 3]])
# 矩阵维度
d = W.shape[0] # 4# 秩
r = 2# 随机初始化 A 和 B
np.random.seed(666)# A 和 B 的元素服从标准正态分布
A = np.random.randn(d, r)
B = np.zeros((r, d))
array([[ 0.82418808, 0.479966 ],[ 1.17346801, 0.90904807],[-0.57172145, -0.10949727],[ 0.01902826, -0.94376106]])
array([[0., 0., 0., 0.],[0., 0., 0., 0.]])
# 定义超参数lr = 0.01 # 学习率,用于控制梯度下降的步长。epochs = 1000 # 迭代次数,进行多少次梯度下降更新。
# 定义损失函数def loss_function(W, A, B):'''W:目标矩阵A:矩阵分解中的一个矩阵,通常是随机初始化的。B:矩阵分解中的另一个矩阵,通常是零矩阵初始化的。'''# 矩阵相乘,@是Python中的矩阵乘法运算符,相当于np.matmul(A, B)。W_approx = A @ B# 损失函数越小,表示 A 和 B 的乘积 W_approx越接近于目标矩阵 Wreturn np.linalg.norm(W - W_approx, "fro")**2 #使用均方误差# 定义梯度下降更新
def descent(W, A, B, lr, epochs):'''梯度下降法'''# 用于记录损失值loss_history = []for i in range(epochs):# 计算梯度W_approx = A @ B# 计算损失函数关于矩阵A的梯度gd_A = -2 * (W - W_approx) @ B.T# 计算损失函数关于矩阵B的梯度gd_B = -2 * A.T @ ( W - W_approx)# 使用梯度下降更新矩阵A和BA -= lr * gd_AB -= lr * gd_B# 计算当前损失loss = loss_function(W, A, B)loss_history.append(loss)# 每100个epoch打印一次if i % 100 == 0:print(f"Epoch: {i} , 损失: {loss:.4f}")# 返回优化后的矩阵return A, B, loss_history# 进行梯度下降优化A, B, loss_history = descent(W, A, B, lr, epochs)
Epoch: 0 , 损失: 87.6534
Epoch: 100 , 损失: 2.3620
Epoch: 200 , 损失: 2.3566
Epoch: 300 , 损失: 2.3566
Epoch: 400 , 损失: 2.3566
Epoch: 500 , 损失: 2.3566
Epoch: 600 , 损失: 2.3566
Epoch: 700 , 损失: 2.3566
Epoch: 800 , 损失: 2.3566
Epoch: 900 , 损失: 2.3566
可以看到loss一直在下降,但是由于这个例子比较简单,loss到2.3620就不再下降了
# 绘制损失曲线
import matplotlib.pyplot as pltplt.figure(figsize=(8,6))
plt.plot(loss_history, label="loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Loss Curve")
plt.legend()
plt.grid(True)
plt.show()
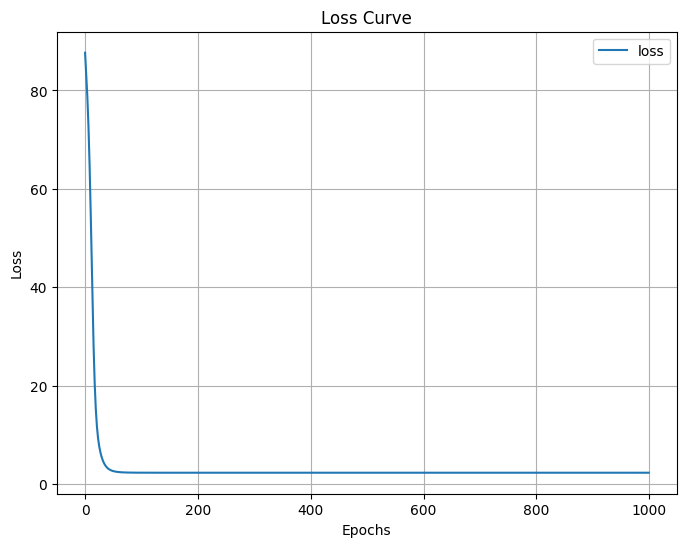
从损失曲线也可以看出,loss是一直下降的,到达最低点后保持不变了
# 最终的近似矩阵
W_approx = A @ Bprint(W_approx)
[[ 3.92499196 3.06584542 2.10616302 0.84487308][ 1.80749375 2.16899061 2.27246474 1.60187065][ 1.39233235 2.65559308 3.44471033 2.81139716][-0.31000446 1.27213581 2.43876645 2.35886822]]
# 原始的矩阵 Wprint(W)
[[4 3 2 1][2 2 2 2][1 3 4 2][0 1 2 3]]
可以看到近似矩阵和原始矩阵值十分接近,所以说这个微调效果还是比较好的
