双目测距实战3-立体匹配

为什么需要立体匹配？

现在给你一张拍出的图像，随意选择一点，你知道这个点在世界坐标吗，或者你知道这个点距离相机多远吗？

在标定过程中，给定3D中的一个点，根据内外参数可以计算出其在图像中坐标，但是从2D到3D缺一个射线方程。

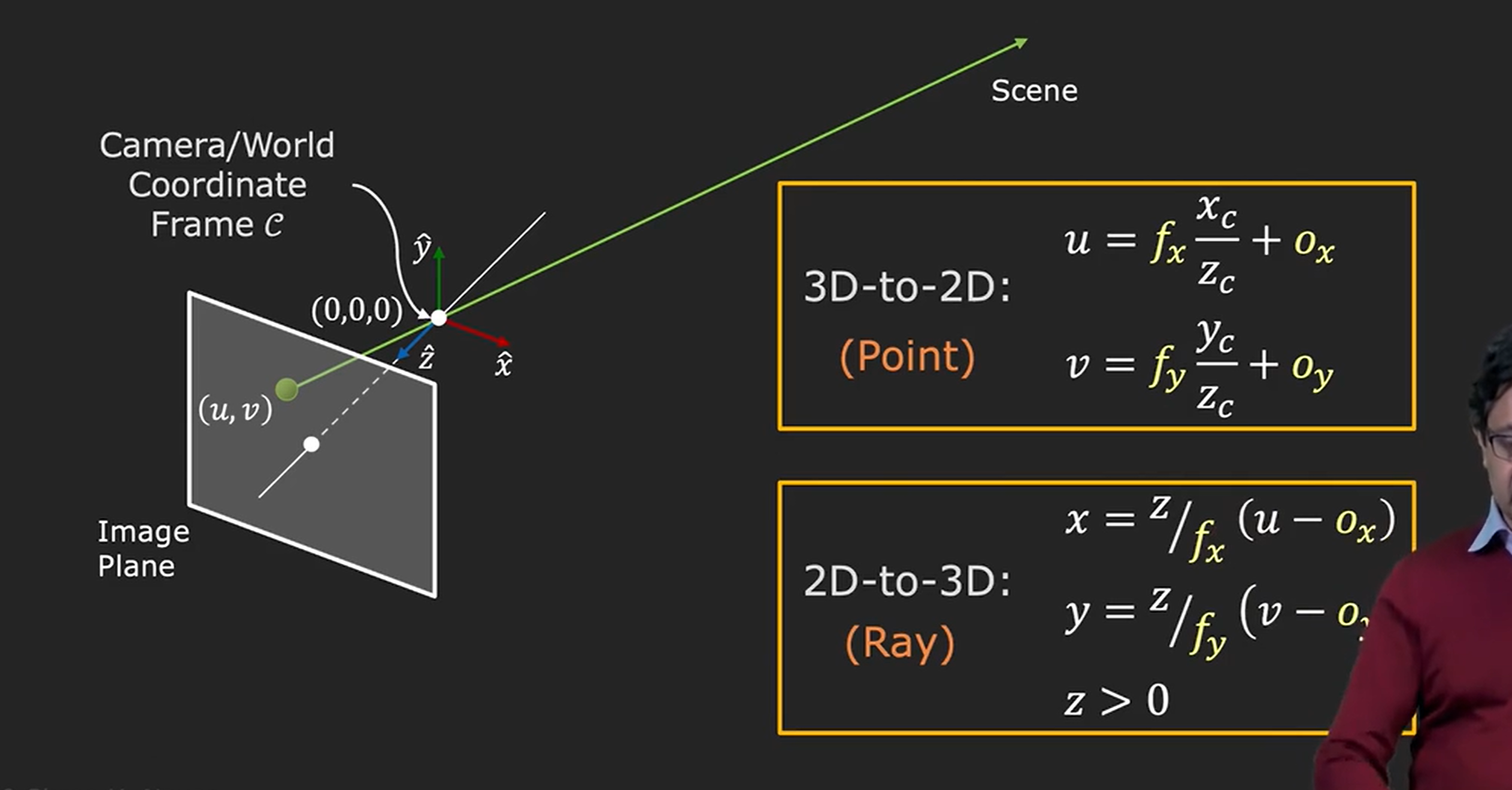
因此为了重建3D，需要给出更多信息，最简单的一个方式就是使用两台相机拍摄两张图像。，同一个点经过光轴交汇点就是场景所在地。

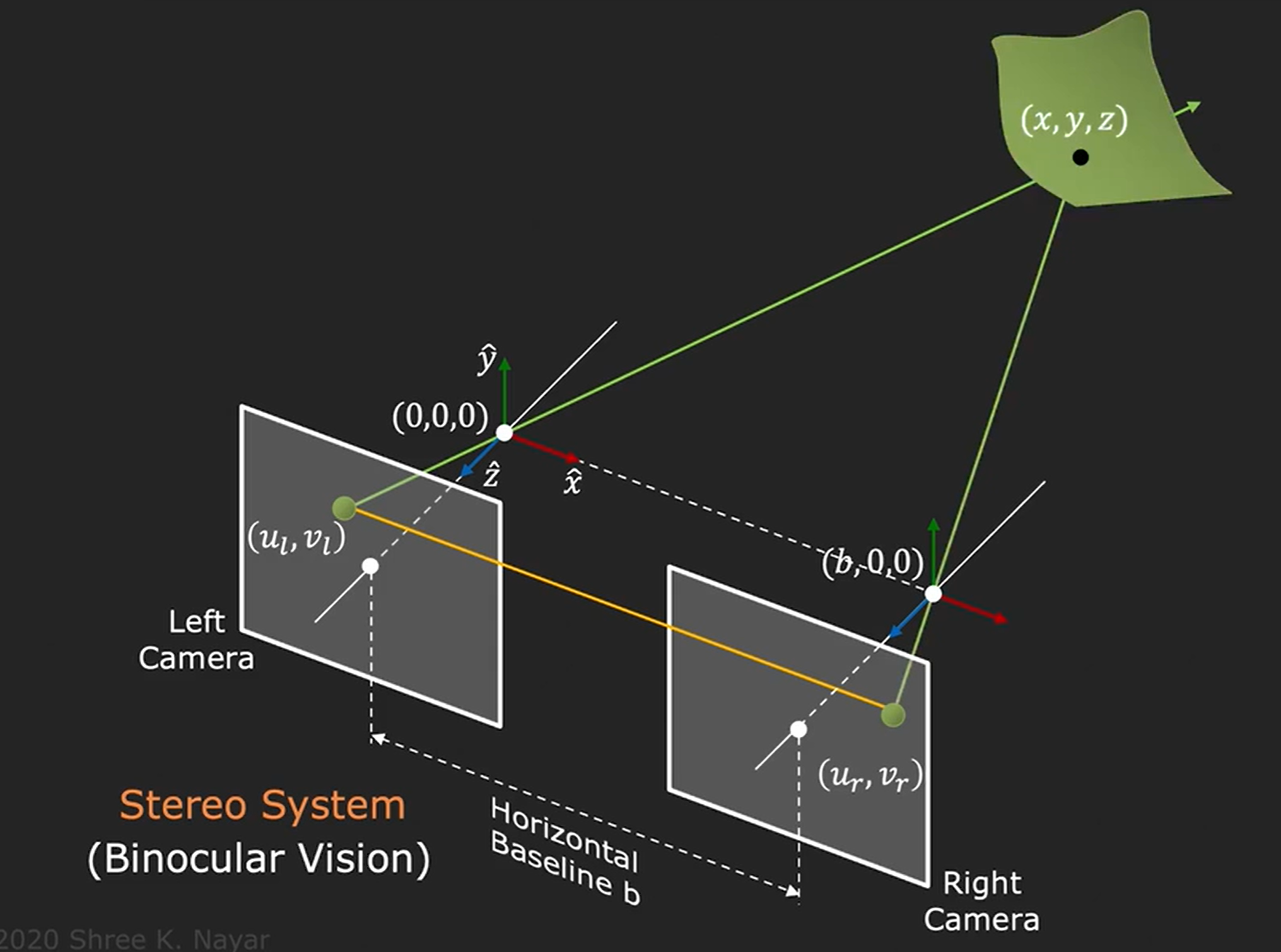
这里的隐藏着一个假设，就是我们已经找到(ul,vl)对应的右坐标系（ur,vr）****，因此这也就是为什么需要匹配。所谓匹配其实就是寻找对应点。

计算三维坐标过程

当知道了两个像素坐标点，可以建立四个方程组，fx fy ox oy已知

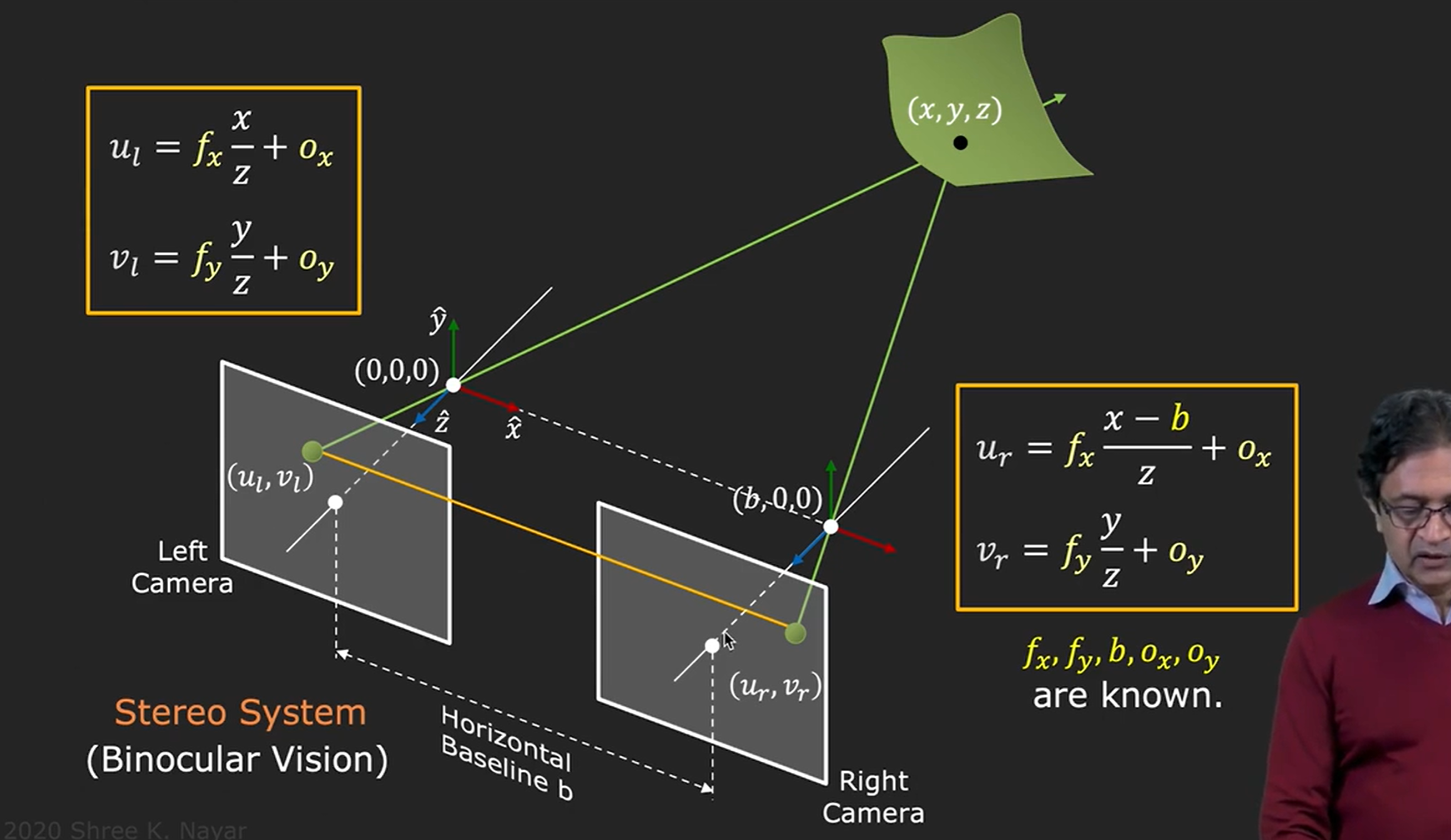
因此可以推导出（x y z）

可以看出视差和深度成反比，当你把一根手指放在离眼睛比较近的地方，你先后睁开左右眼，可以明显感觉到手指跳动了一下，但是把手指放在远处，感觉就不会那么强烈，离得越近，视差越大。

在设计立体匹配系统时，基线设置的越大，产生的视差也就越大

立体匹配

右边的图为视差图，用于评估结果。对于拍出的一个两张图片，任意一点在垂直方向应该是不会变化的，只有左右变化

传统算法

定义一个窗口，沿着横轴滑动查找，在定义相似上，有各种方式。

深度学习算法

基于深度学习的算法又分为稀疏匹配和稠密匹配。假如我想计算任意一点的深度信息，且图像是矫正的。SGBM这类方法是用于计算“图中所有像素”的深度的，它是一种稠密匹配方法。用它来只计算“任意一点”的深度，就像“用牛刀杀鸡”——虽然可行，但完全没有必要，而且效率低下，方法也不够直接。

下面我们来详细剖析这个问题。

一、 SGBM是什么？它如何工作？

SGBM (Semi-Global Block Matching) 是一种经典的稠密立体匹配算法。

• 目标：为左图中的每一个像素，在右图的对应极线（校正后就是同一行）上找到最佳匹配点，从而计算出整张图像的视差图 (Disparity Map)。
• “稠密”的含义：它试图为图像中几乎所有的像素点都计算出视差，最终输出一个与原图一样大小的视差图。
• 工作原理特点：
  1. 基于代价计算：它不仅仅是单个像素点的比较，而是比较一个小的像素块（Block Matching）的相似度。
  2. 半全局约束：这是SGBM的核心。它不孤立地看待每个像素的匹配，而是引入了一个“平滑性”假设：即相邻的像素，其视差值也应该是相近的。它通过动态规划，从多个方向（通常是8个或16个）累积匹配代价，从而找到一个全局最优（或近似最优）的解。这使得它在弱纹理和重复纹理区域的表现要优于单纯的块匹配。

结论：SGBM的设计初衷就是为了生成一张完整的、稠密的视差图。

二、 用SGBM计算“任意一点”深度的问题

如果你想用SGBM来计算图中某一个特定点 (u, v) 的深度，你需要：

1. 运行完整的SGBM算法，计算出整张图的视差图。
2. 从生成的视差图中，读取 (u, v) 位置的视差值 d。
3. 使用公式 Z = (f * B) / d 计算该点的深度。

这种方法的弊端显而易见：

• 计算浪费：为了得到一个点的深度，你计算了整幅图像（比如百万像素级别）的深度，其中99.999%的结果你都用不上。
• 结果不一定准确：SGBM的半全局平滑约束，可能会为了保证整体视差图的平滑性，而牺牲单个点的局部精度。也就是说，它在该点计算出的视差，是综合了周围邻域信息和全局约束后的结果，不一定是该点最精确的“局部最优”匹配。

三、 计算“任意一点”深度的正确方法：稀疏匹配

如果你只需要计算图中一个或少数几个特定点的深度，正确且高效的方法是稀疏特征匹配 (Sparse Feature Matching)。

这种方法只关心那些“特征明显”的点，比如角点、斑点等。

计算步骤如下：

1. 确定目标点：指定你想要计算深度的点，例如用户鼠标点击的点 p_l = (u_l, v_l)。
2. 特征提取与描述：
   • 在点 p_l 周围取一个小区域（Patch），例如15x15的像素块。
   • 为这个小区域计算一个特征描述子 (Feature Descriptor)。描述子就像这个区域的“指纹”，它对光照变化、轻微旋转等不敏感。简单的方法可以直接使用像素块本身，但更鲁棒的方法是使用SIFT, SURF, ORB等算法来生成描述子。
3. 特征匹配：
   • 在右图的对应行 v_l 上，进行一维搜索。
   • 在搜索路径上的每一个可能位置 u_r，同样取一个同样大小的像素块，并计算其特征描述子。
   • 比较左图目标点的描述子和右图搜索路径上所有点的描述子，找到相似度最高（即描述子距离最近）的点 p_r = (u_r, v_l)，这个点就是最佳匹配点。
4. 计算深度：
   • 计算视差 d = u_l - u_r。
   • 使用公式 Z = (f * B) / d 计算深度。

稠密匹配VS稠密匹配

• 稀疏匹配只能告诉你空间少数几个、孤立的特征点的三维坐标
• 稠密匹配为你提供全场景的深度信息
• 使用稠密匹配，你可以将从不同角度拍摄的双目图像序列融合成一个完整的、带有真实纹理的三维模型。这被广泛应用于数字城市、文物保护、游戏场景制作等领域。稀疏匹配只能重建出一个场景的“骨架”，而稠密匹配则能恢复出它的“血肉”。
• 对于测距（计算图中任意两点的距离）其实还是稀疏匹配最具性价比
• 稠密匹配要求图像必须是矫正后的，但稀疏匹配是可以的，这是因为在相机标定中，会生成一个强大的几何工具：**基本矩阵，**它可以计算出对极线，沿着这条对极线去搜索就可以

四、 总结与对比

方法	SGBM (稠密匹配)	稀疏特征匹配
核心思想	计算图中所有点的视差，追求全局最优和结果的平滑性。	只计算特定兴趣点的视差，追求该点匹配的局部最优。
是否必须	不是。对于计算单点深度来说，它是一种错误的方法。	是。这是计算稀疏点深度的标准和高效方法。
输入	整对左右校正图像。	一对校正图像 + 一个指定的左图坐标点。
输出	一张完整的视差图。	一个视差值，或者一个匹配点对。
计算成本	高。需要处理整幅图像。	极低。只涉及少量特征计算和一维搜索。
适用场景	生成稠密深度图、三维场景重建、机器人导航避障。	视觉SLAM中的特征点跟踪、物体测量、AR中的目标定位。

关于匹配算法，可以参考网站。

立体矫正

从纯数学原理上讲，只要有准确的内外参，即使图像不经过矫正，也完全可以进行测深。

一、 三角测量的本质

三角测量的本质是一个几何问题：已知两个（或多个）不同视角的观测点（相机光心），以及一个三维空间点在这几个视角成像平面上的投影坐标，求解这个三维空间点的坐标。

要完成这个计算，你只需要以下信息：

1. 相机的内参矩阵 (K)：描述相机自身的成像特性。
2. 相机的外参 (R 和 T)：描述两个相机之间的相对旋转和平移。
3. 一对匹配好的对应点：即空间中同一个点在左右两幅图像中的像素坐标 (u, v) 和 (u’, v’)。

只要这三个条件具备，无论图像是否经过矫正，我们都可以通过求解线性方程组来计算出该点的三维坐标。这个过程在数学上是始终成立的。

另外有了矫正图像，其测深计算方法从一个通用的、相对复杂的线性代数求解问题，变成一个直接利用一个叫是视差图的关键量

二、 既然如此，为什么我们还要大费周章地进行图像矫正？

答案在于上述第3个条件——“一对匹配好的对应点”。

对于三角测量，我们可以手动指定对应点。但对于计算机视觉来说，我们的目标是计算出图像中成千上万个像素点的深度，形成一张稠密的深度图。这就引出了一个核心难题：立体匹配 (Stereo Matching)。

立体匹配的目的就是为左图中的每一个像素，在右图中找到它的同名点。

• 在未矫正的图像中进行匹配：
  • 根据对极几何约束，左图的一个点，它在右图中的对应点一定位于一条被称为**“极线”**的直线上。
  • 在未矫正的情况下，这条极线可以是倾斜的任意直线。
  • 这意味着，为了给左图的一个点找到匹配，算法需要在右图中沿着一条倾斜的线进行搜索。这使得搜索过程非常复杂，计算量巨大，且容易出错。
• 在矫正后的图像中进行匹配：
  • 图像矫正的核心目的就是将所有的极线都变成水平的，并且让左右图像的极线位于同一行。
  • 这意味着，左图中的点 (u, v)，它在右图中的对应点必定位于同一水平线（同一行）v上。
  • 这样一来，匹配搜索的维度就从二维（在倾斜的线上搜索）降低到了一维（在单行像素内搜索）。算法只需要在右图的同一行从左到右扫描，寻找最佳匹配点即可。
• 未矫正的匹配：就像在一个杂乱无章的图书馆里找一本书，你只知道它在某个倾斜的书架上，你得歪着头顺着书架找。
• 矫正后的匹配：就像在一个排列整齐的图书馆里找书，你知道它就在你面前这一排的某个位置，你只需水平扫视就能找到。