【小白笔记】理解 PyTorch 和 NumPy 中的张量（Tensor）形状变化unsqueeze(0)

1. unsqueeze(0)

• 英文词源和解释：

  • Squeeze (挤压，压缩)：这个词源自中古英语的 queisen，指用力压、挤出汁液或缩小体积。在 PyTorch 中，tensor.squeeze() 的作用正是移除张量中所有尺寸为 1 的维度（进行压缩）。
  • Un-squeeze (非挤压，展开)：
    • Un- 是一个常见的否定前缀，表示“不”、“非”或“做相反的动作”（例如：unhappy, undo）。
    • Unsqueeze 就是 Squeeze 的反向操作，即展开、扩充。
  • 在 PyTorch 中： unsqueeze() 的意思就是**“展开一个维度”或“增加一个尺寸为 1 的维度”**。

• 记忆点： squeeze 是压缩维度；unsqueeze 是展开维度。

---

2. unsqueeze(0) 是具体怎么加的？为什么就变成一个矩阵了？哪个方向加呢？

我们来用具体的矩阵形状和“人话”来形象化地解释 unsqueeze(0) 为什么是广播的关键，以及它如何将一个向量逻辑上变成一个矩阵。

形象化解释：unsqueeze(0) 与广播

假设我们的数据非常简单：每个样本只有 3 个特征。

1. 我们的目标：距离计算

我们要计算：新样本 $x_{\text{new}}$ 与 训练集 $X_{\text{train}}$ 中的所有样本 的特征差。

2. 原始形状（Python 和 PyTorch 的默认表示）

• 新样本 $x_{\text{new}}$（向量）：

  • 表示：[f1, f2, f3]
  • 形状 (Shape)：(3,)
  • 人话：这是一个一维数组，PyTorch 默认把它当做 3 个元素的列表。

• 训练集 $X_{\text{train}}$（矩阵）：

  • 假设有 5 个训练样本。
  • 表示：
    $$\left(\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& c_2& c_3\\ d_1& d_2& d_3\\ e_1& e_2& e_3\end{array}\right)$$
  • 形状 (Shape)：(5, 3)
  • 人话：这是一个 5 行 3 列的表格。

3. 失败的尝试：不使用 unsqueeze

如果直接计算 X_train - x_new，PyTorch 会报错或给出意想不到的结果，因为它不知道如何对齐 (5, 3) 和 (3,)。

4. 关键步骤：x_new.unsqueeze(0)

我们对新样本 $x_{\text{new}}$ 执行 unsqueeze(0)：

• 动作： 在第 0 轴（最前面）添加一个尺寸为 1 的新维度。
• 新形状 $x_{\text{new\_expanded}}$：(1, 3)
• 形象化表示（行向量矩阵）：
  $$\left(\begin{array}{ccc}{f}_1& f_2& f_3\end{array}\right)$$
  • 人话：它从一个“列表”变成了一个“只有 1 行的表格”。

为什么是“从列表到只有 1 行的表格”？

人话解释： 在编程语境中，一个向量（一维数组）在数据结构上非常像一个 Python 列表。当我们执行 unsqueeze(0) 时，我们是在逻辑上将它升级成一个矩阵（二维数组，也就是“表格”）。

详细解释：

1. 原始状态（形状 (3,)）：

   • 数据： [f1, f2, f3]
   • Python 视角： 这就是一个列表或者说是一个一维数组。在 PyTorch 中，它的形状是 (3,)，代表只有 3 个元素，没有“行”或“列”的概念。
   • 数学视角： 这是一个向量。

2. unsqueeze(0) 之后（形状 (1, 3)）：

   • 动作： 在最前面（第 0 轴）加入了数字 1。
   • 新数据： [[f1, f2, f3]]
   • Python/PyTorch 视角： 这是一个二维数组。它的形状是 (1, 3)，意味着它有 1 行和 3 列。
   • 形象化： 任何具有 (行数, 列数) 形状的结构，本质上就是一个表格（矩阵）。所以，一个 1 行的二维数组就是“只有 1 行的表格”。

关键点：数据格式的转换

格式/类型	形状	维度 (Dimension)	形象化
Python 列表	不适用	N/A	[f1, f2, f3]
原始张量	(3,)	1 维 (Vector)	[f1, f2, f3]
unsqueeze(0) 后	(1, 3)	2 维 (Matrix)	[[f1, f2, f3]] (1行3列的表格)

总结：

• 并不是说原始张量是 Python 的 list 格式，而是说，它的一维形状 (3,) 在概念上类似于列表。
• unsqueeze(0) 的作用是赋予它二维的身份 ((1, 3))，这个身份（1 行的表格）是激活广播机制所需要的，因为它现在可以和训练集的 (N, 3) 矩阵进行行级别的对齐了。

5. 广播机制 (Broadcasting) 的发生

现在我们要计算 $X_{\text{train}}$ 减去 $x_{\text{new\_expanded}}$：

• 运算： $X_{\text{train}}(5,3)-x_{\text{new\_expanded}}(1,3)$

• 广播的逻辑：

  1. 比较右侧维度： 都是 3，完美匹配。
  2. 比较左侧维度： 左边是 5，右边是 1。当其中一个维度是 1 时，就可以进行广播！
  3. PyTorch 的动作： PyTorch 会逻辑上（不复制内存）将 $x_{\text{new\_expanded}}$ 沿着第 0 轴（行方向）复制 5 次，使它的形状也变成 (5, 3)。

• 最终运算效果：

  

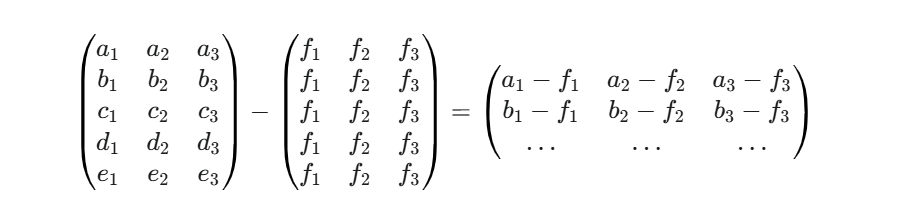
总结：为什么是关键？

unsqueeze(0) 就是给单个样本加上一个 “我是批量” 的维度（即尺寸为 1 的第 0 维）。这使得 PyTorch 能够识别出：“哦，你这是要用这一行数据去对齐并处理所有行。” 从而高效地在不写循环的情况下，计算出新样本与所有训练样本的特征差。

“在第 0 个位置（最前面）增加一个维度”这个动作，是在张量形状的逻辑结构上发生的，而不是物理数据本身的改变。

A. 为什么变成矩阵？（维度的变化）

在张量（或 NumPy 数组）中：

张量术语	形状 (Shape)	含义
向量 (Vector)	(N,)	一维，通常代表一个样本
矩阵 (Matrix)	(N, M)	二维，通常代表 N 个样本，每个样本 M 个特征
更高维张量	(A, B, C, ...)	三维或更高维

关键记忆点： unsqueeze(0) 就是给张量穿上一个“外套”，从 (特征数) 变成 (1, 特征数)，从而让它具备了批量处理的资格，能够与整个数据集进行广播运算。