大模型微调(一):有监督微调与困惑度
经过预训练后,模型的参数有数十亿个,它们形成了一个向量:
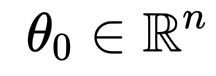
\theta_0 \in \mathbb{R}^n
它编码了模型所学到的一切关于语言的知识:结构、语义、节奏。但这些权重是通用的,而非个性化的。模型此刻知道单词的含义,但不知道如何使用它们来表达善意、安全或清晰。
然后是有监督微调:
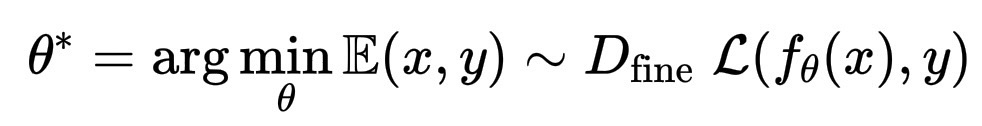
\theta^* = \arg\min_{\theta} \mathbb{E}{(x, y) \sim D_\text{fine}} \; \mathcal{L}(f_\theta(x), y)
这里,D_{fine} 就像是课堂,一个精心挑选的数据集,包含类人对话、推理示例和来自人类的反馈。每一对 (x, y) 不仅教会模型预测下一个标记,还教会模型如何根据意图调整回答。
接下来是另一个步骤,从人类反馈中强化学习 (RLHF),在这个过程中,模型的行为不再受标签的影响,而是由偏好决定。在这里,了解到一个答案可能比另一个答案更有帮助、更真实或更温和。
从数学上讲,它看起来像:
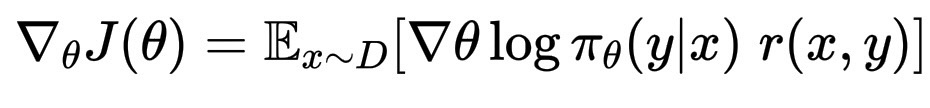
\nabla_\theta J(\theta) = \mathbb{E}_{x \sim D} \left[ \nabla\theta \log \pi_\theta(y|x) \; r(x,y) \right]
其中 r(x,y) 是人类的偏好,表现良好的“奖励”,而 \pi_\theta 是控制模型说话方式的策略。
这一切之下,打个比方,就像是学习辨别颜色:预训练给出了颜色的定义,微调赋予它们温暖,而 RLHF 教会了模型是什么颜色让人微笑、犹豫或叹息。
微调的第一步在数学上几乎与预训练完全相同。它仍然使用梯度下降,或者更准确地说,是随机梯度下降及其变体,如 Adam 或 Adafactor。核心流程保持不变:
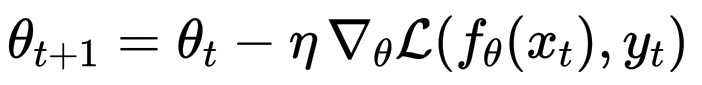
\theta_{t+1} = \theta_t - \eta \, \nabla_\theta \mathcal{L}(f_\theta(x_t), y_t)
每次更新都会将参数 \theta 在损失函数曲面上略微向下移动,就像在预训练中一样。区别不在于机制,而在于地形和意图:
- 数据集 (D_\text{fine}):它不是从现实世界中抓取的文本海洋,而是一个湖泊,更小,但更清澈。这些是对话、解释、指令,它们教会模型说话和推理,而不仅仅是背诵。
- 损失函数 (\mathcal{L}):通常仍然是交叉熵,但有时会调整以衡量指令执行的质量,而不仅仅是标记预测。
- 学习率 (\eta):更小,因为目标不是覆盖预训练知识,而是对其进行打磨,在不丢失模型已经学到的广泛知识的情况下对其进行温和的调整。
可以想象一下这个过程:在预训练期间,优化就像用未经加工的大理石雕刻一个巨大的雕像,用大锤子敲打。在微调期间,优化换成了凿子,完善细节,柔化边缘,并赋予雕像表情。
即使在有监督微调中,事情也可能出错或出现不可预测的变化。损失函数仍然是指南针,但它并不总是能说明全部情况。此外,在这个阶段,我们很少直接使用 Hessian 矩阵。
在微调过程中,损失函数仍然是进度的主要指标,它衡量的是,在给定指令 x_i 的情况下,模型复现人类给出的响应 y_i 的准确率。
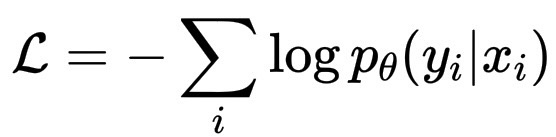
\mathcal{L} = - \sum_i \log p_\theta(y_i | x_i)
但仅凭这个标量损失并不能涵盖所有内容。因此,工程师还会:
- 在保留的验证集上评估模型的响应,以避免过拟合。
- 测量困惑度、准确率和指令遵循指标。
- 偶尔定性地检查生成的输出,像阅读论文一样阅读它们,而不仅仅是数字。
这是数值观察和人工观察的结合,既需要显微镜,也需要人眼的观察。
Hessian矩阵是一个二阶导数矩阵,它描述了损失曲面的局部曲率,因此理论上它非常有用。它可以告诉权重是处于一个宽阔、稳定的盆地(良好的泛化能力),还是一个狭窄、尖锐的盆地(脆弱的学习能力)。
但问题在于,对于拥有数十亿个参数的模型,H 将包含数万亿个条目。这实在太大,无法计算或存储。因此,在微调过程中,我们不会直接计算它。相反,我们通过观察损失如何逐步变化来间接推断曲率:
- 如果损失振荡或发散,学习率可能过高或谷底过陡。
- 如果损失稳步下降并趋于稳定,我们很可能正在下降到一个平滑且可泛化的谷底。
当模型预测一个序列中的下一个标记时,比如,在读完“遇见你让我……”之后,模型会为所有可能的后续单词分配概率:
p_\theta(高兴) = 0.7, p_\theta(难过) = 0.05, p_\theta(迷惑) = 0.02, ……
如果模型的预测准确且自信,“高兴”占据了大部分概率,这意味着模型对这个模式理解得很好。如果模型的预测很分散且不确定,所有单词的概率都差不多,模型就是“困惑的”(perplexity)。
困惑度的正式定义如下:
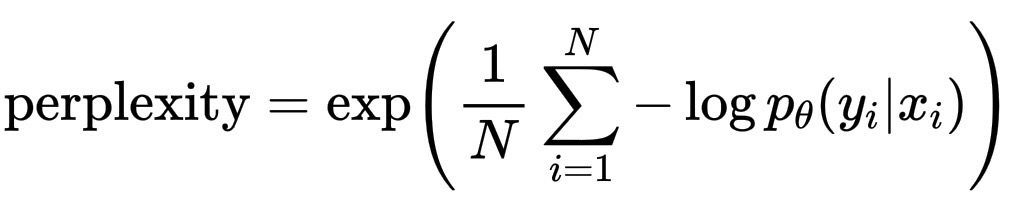
\text{perplexity} = \exp\left( \frac{1}{N} \sum_{i=1}^N -\log p_\theta(y_i|x_i) \right)
它实际上是平均惊讶度的指数。
因此,低困惑度对模型意味着:“我并不惊讶,我理解这个世界。”
高困惑度对模型意味着:“这个序列让我感到困惑,我不知道接下来该说什么。”
近似曲率能揭示困惑度问题吗?可以间接地揭示:
- 曲率(通过 Hessian 矩阵或其近似值)告诉我们损失函数对参数变化的敏感度。
- 困惑度告诉我们模型预测的不确定性。
当曲率非常陡峭(谷值较窄)时,微小的参数变化会导致损失函数大幅跳跃,模型不稳定且经常过拟合,新数据的困惑度上升。当曲率宽阔平滑时,模型泛化能力更强,未知文本的困惑度保持较低水平。
