「深度学习笔记3」概率论深度解析:从不确定性到人工智能的桥梁
1. 概率论:理解不确定世界的数学语言
概率论其实就是一门研究事情发生的可能性的学问。想象一下,明天会不会下雨?抛硬币是正面还是反面?这些都是我们日常生活中遇到的不确定性问题。概率论就是帮我们量化这种不确定性的工具,让我们能在随机世界中做出理性判断。
1.1 为什么概率论对深度学习如此重要?
在AI和深度学习火热的今天,概率论可是扮演着超级重要的角色!它就像是深度学习的数学基础和实用工具的结合体。
简单来说,概率论在深度学习中有三大作用:
- 不确定性建模:让AI知道自己有多"不确定"
- 决策优化:帮AI选择最优方案
- 算法基础:很多高级AI算法都建立在概率论上
2. 概率论的核心概念体系
2.1 概率论的"三大定律"
概率论建立在三个基本公理上,就像是数学世界的"宪法":
- 非负性:概率值不能是负数,P(A)≥0P(A) \geq 0P(A)≥0
- 规范性:所有可能结果的概率之和等于1,P(Ω)=1P(\Omega) = 1P(Ω)=1
- 可加性:互斥事件的概率可以相加
2.2 理解概率的三种视角
| 概率类型 | 怎么理解 | 生活例子 | 适用场景 |
|---|---|---|---|
| 古典概率 | 等可能性 | 掷骰子每个面概率都是1/6 | 游戏、抽签 |
| 频率概率 | 长期频率 | 抛1000次硬币,正面大约500次 | 质量控制、保险 |
| 主观概率 | 个人信念 | 明天有80%概率下雨 | 商业决策、医疗诊断 |
3. 条件概率与贝叶斯定理:AI的"思考方式"
3.1 条件概率:已知某些信息后的概率
条件概率就是在已知某些信息的情况下,事件发生的概率。公式是:
P(A∣B)=P(A∩B)P(B)P(A|B) = \frac{P(A \cap B)}{P(B)}P(A∣B)=P(B)P(A∩B)
举个例子:已知今天乌云密布(BBB),那么下雨的概率(AAA)就是条件概率P(A∣B)P(A|B)P(A∣B)。
3.2 贝叶斯定理:从结果反推原因
贝叶斯定理是概率论中的"超级明星",公式为:
P(A∣B)=P(B∣A)⋅P(A)P(B)P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}P(A∣B)=P(B)P(B∣A)⋅P(A)
这个公式的厉害之处在于它能让我们根据新证据更新信念。比如在医疗诊断中:
- P(疾病)P(疾病)P(疾病)是患病率(先验概率)
- P(阳性∣疾病)P(阳性|疾病)P(阳性∣疾病)是检测准确率
- P(疾病∣阳性)P(疾病|阳性)P(疾病∣阳性)是检测阳性后真正患病的概率(后验概率)
3.3 全概率公式:化整为零的智慧
全概率公式的核心理念是"分而治之":
P(A)=∑P(Bi)⋅P(A∣Bi)P(A) = \sum P(B_i) \cdot P(A|B_i)P(A)=∑P(Bi)⋅P(A∣Bi)
就是把复杂问题分解成多个简单部分,分别解决后再组合起来。
4. 概率分布:随机现象的"身份证"
概率分布描述了随机变量取不同值的概率规律。
4.1 离散型概率分布
伯努利分布:就像抛一次硬币,只有两种结果(成功/失败) P(X=1)=pP(X=1) = pP(X=1)=p, P(X=0)=1−pP(X=0) = 1-pP(X=0)=1−p
二项分布:抛n次硬币,正面出现次数的分布
泊松分布:描述稀有事件的发生次数,比如每分钟接到电话的次数
4.2 连续型概率分布
正态分布(高斯分布):自然界中最常见的分布,比如人群的身高分布
f(x)=1σ2πe−(x−μ)22σ2f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=σ2π1e−2σ2(x−μ)2
5. 概率论在AI中的实际应用
5.1 朴素贝叶斯分类器:垃圾邮件过滤的功臣
朴素贝叶斯是贝叶斯推理在文本分类中的经典应用。虽然它做了"条件独立"的简化假设(即认为词语之间相互独立),但在实际中效果出奇的好!
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
import jieba# 模拟邮件数据集
emails = [# 垃圾邮件样本 (标签为1)"免费获得 iPhone 点击链接 赢取大奖","赢取百万大奖立即参与 限时优惠","限时优惠不要错过 低价促销","恭喜中奖 领取奖金 点击链接","打折促销 买一送一 最后机会","低价商品 限量抢购 立即下单","免运费 特大优惠 不要错过","现金奖励 点击领取 优惠活动",# 正常邮件样本 (标签为0) "明天会议安排请查收 项目讨论","项目报告已发送请审阅 工作总结","周末团建活动通知 团建安排","月度工作计划请查看 工作安排","财务报表已发送 请查收审核","下周日程安排 请确认时间","公司培训通知 请大家参加","项目进度汇报 请审阅修改"
]labels = [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0] # 1:垃圾邮件, 0:正常邮件# 自定义中文分词函数
def chinese_tokenizer(text):return jieba.lcut(text) # 精确模式分词# 创建管道,指定分词器并尝试引入N-gram特征(如bigram)
model = make_pipeline(CountVectorizer(tokenizer=chinese_tokenizer,token_pattern=None, # 禁用默认token_patternngram_range=(1, 2)), # 同时考虑单个词和相邻的两个词组合MultinomialNB(alpha=0.5) # 可尝试调整平滑强度,例如0.5
)
model.fit(emails, labels)# 预测新邮件
test_emails = ["优惠活动进行中", "月度工作总结"]
predictions = model.predict(test_emails)
probabilities = model.predict_proba(test_emails)print("完整概率矩阵:")
print(probabilities)
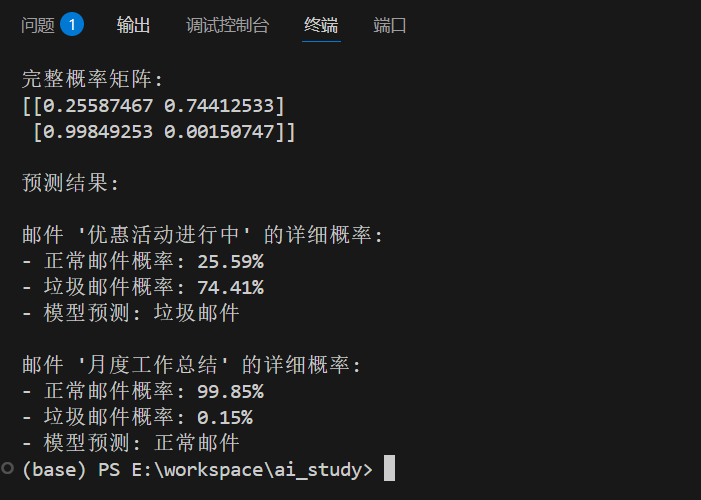
print("\n预测结果:")for i, email in enumerate(test_emails):# 提取垃圾邮件的概率spam_prob = probabilities[i]print(f"\n邮件 '{email}' 的详细概率:")print(f"- 正常邮件概率: {spam_prob[0]:.2%}")print(f"- 垃圾邮件概率: {spam_prob[1]:.2%}")print(f"- 模型预测: {'垃圾邮件' if predictions[i] == 1 else '正常邮件'}")
运行结果:
5.2 天气预报中的贝叶斯推理
def weather_forecast():# 基础概率P_rain = 0.2 # 下雨概率20%P_no_rain = 0.8 # 不下雨概率80%# 条件概率P_clouds_if_rain = 0.8 # 下雨时乌云概率P_clouds_if_no_rain = 0.3 # 不下雨时乌云概率#观察到乌云P_clouds = (P_clouds_if_rain * P_rain + P_clouds_if_no_rain * P_no_rain)# 贝叶斯更新P_rain_if_clouds = (P_clouds_if_rain * P_rain) / P_cloudsreturn P_rain_if_cloudsrain_prob = weather_forecast()
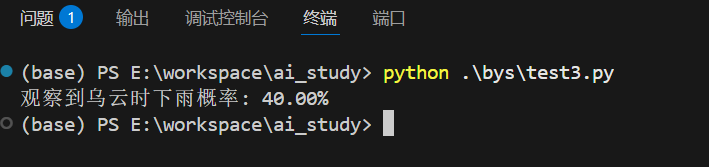
print(f"观察到乌云时下雨概率: {rain_prob:.2%}")
运行结果:
5.3 概率图模型:描述变量间的复杂关系
概率图模型用图的方式直观表示变量间的概率依赖关系,是深度概率模型的基础。
有向图模型(贝叶斯网络)
有向图模型用带箭头的线表示变量间的因果关系,形成一个有向无环图(DAG)。
[季节]↓[感冒]/ \↓ ↓
[发烧] [流鼻涕]
典型应用场景:医学诊断、故障分析等有明确因果关系的领域。
无向图模型(马尔可夫随机场)
无向图模型用不带箭头的线表示变量间的相互作用关系,不区分因果方向。
典型应用场景:图像分割、社交网络分析等变量间相互影响的场景。
实际例子:用Python实现简单贝叶斯网络
下面是一个医疗诊断的贝叶斯网络示例,展示了如何用代码构建概率图模型:
from pgmpy.models import DiscreteBayesianNetwork # 使用正确的类名
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination# 创建贝叶斯网络结构
model = DiscreteBayesianNetwork([('季节', '感冒'), # 季节 → 感冒('感冒', '发烧'), # 感冒 → 发烧 ('感冒', '流鼻涕') # 感冒 → 流鼻涕
])# 定义条件概率分布
# 季节的概率分布(先验概率)
cpd_季节 = TabularCPD(variable='季节', variable_card=4, # 4个季节values=[[0.25], [0.25], [0.25], [0.25]] # 每个季节概率相等
)# 给定季节条件下感冒的概率
cpd_感冒 = TabularCPD(variable='感冒',variable_card=2, # 0:不感冒, 1:感冒values=[[0.9, 0.7, 0.6, 0.8], # 不感冒的概率(春,夏,秋,冬)[0.1, 0.3, 0.4, 0.2] # 感冒的概率],evidence=['季节'],evidence_card=
)# 给定感冒条件下发烧的概率
cpd_发烧 = TabularCPD(variable='发烧',variable_card=2, # 0:不发烧, 1:发烧values=[[0.95, 0.3], # 不感冒时不发烧概率95%,感冒时30%[0.05, 0.7] # 不感冒时发烧概率5%,感冒时70%],evidence=['感冒'],evidence_card=
)# 给定感冒条件下流鼻涕的概率
cpd_流鼻涕 = TabularCPD(variable='流鼻涕',variable_card=2, # 0:不流鼻涕, 1:流鼻涕values=[[0.9, 0.2], # 不感冒时不流鼻涕概率90%,感冒时20%[0.1, 0.8] # 不感冒时流鼻涕概率10%,感冒时80%],evidence=['感冒'],evidence_card=
)# 将概率分布添加到模型中
model.add_cpds(cpd_季节, cpd_感冒, cpd_发烧, cpd_流鼻涕)# 检查模型是否配置正确
print("模型检查:", model.check_model())# 进行概率推理[1]
inference = VariableElimination(model)# 例子1:已知是冬季,计算感冒的概率
result1 = inference.query(variables=['感冒'], evidence={'季节': 3}) # 3代表冬季
print("冬季感冒概率:", result1)# 例子2:已知患者流鼻涕,推断感冒的概率
result2 = inference.query(variables=['感冒'], evidence={'流鼻涕': 1})
print("流鼻涕时感冒概率:", result2)# 例子3:已知发烧且流鼻涕,推断感冒的概率
result3 = inference.query(variables=['感冒'], evidence={'发烧': 1, '流鼻涕': 1})
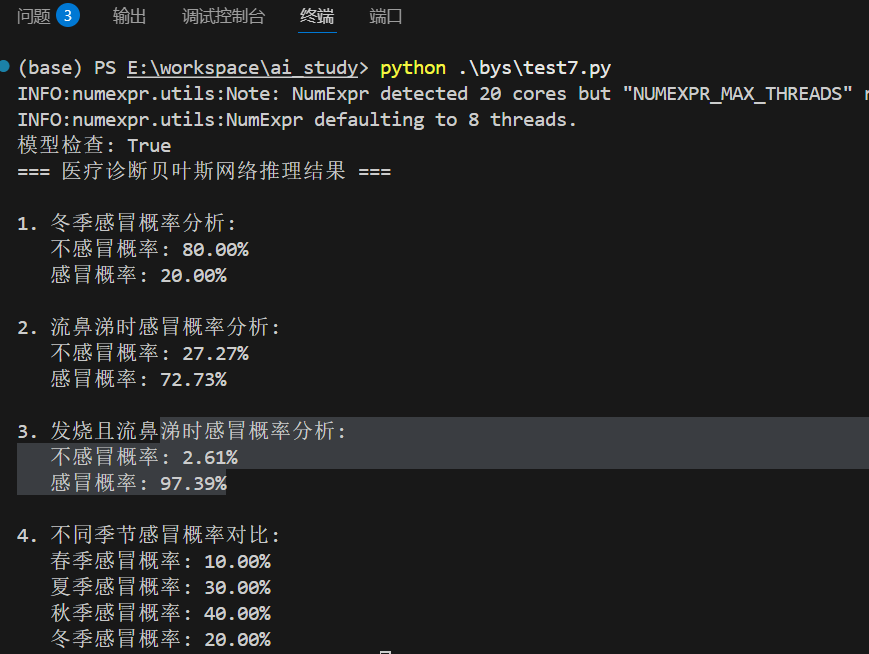
print("发烧且流鼻涕时感冒概率:", result3)
运行结果:
6. 实际案例:医疗诊断中的贝叶斯推理
假设某种疾病在人群中的患病率是1%,检测方法的准确率是99%。那么检测阳性时真正患病的概率是多少?
def medical_bayes():# 先验概率P_disease = 0.01 # 患病率1%P_healthy = 0.99 # 健康率99%# 条件概率P_positive_if_disease = 0.99 # 患病者检测阳性概率P_positive_if_healthy = 0.01 # 健康者误检阳性概率# 全概率公式计算检测阳性的总概率P_positive = (P_positive_if_disease * P_disease + P_positive_if_healthy * P_healthy)# 贝叶斯公式计算后验概率P_disease_if_positive = (P_positive_if_disease * P_disease) / P_positiveprint(f"即使检测呈阳性,真正患病的概率也只有: {P_disease_if_positive:.2%}")medical_bayes()
运行结果:
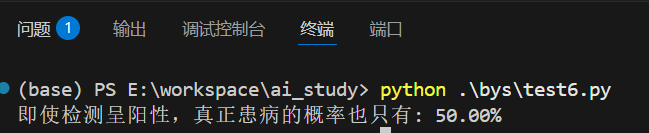
这个结果往往让人惊讶:即使检测准确率高达99%,检测阳性时真正患病的概率也只有50%左右!这就是贝叶斯定理的反直觉之处。
总结
概率论不仅仅是数学公式的集合,更是一种思维方式。它教会我们:
✅ 拥抱不确定性:世界本质是不确定的,我们要学会与之共处
✅ 持续更新信念:根据新证据调整判断,保持开放心态
✅ 量化决策:用数据而不是直觉做决策
✅ 分而治之:复杂问题分解为简单部分
正如著名数学家拉普拉斯所说:“概率论本质上只是化简为计算的常识。” 在这个数据驱动的时代,掌握概率论就是掌握了理解复杂世界的一把钥匙。
