强化学习_Paper_2000_Eligibility Traces for Off-Policy Policy Evaluation
paper Link: Eligibility Traces for Off-Policy Policy Evaluation
1. 问题设定
- 行为策略 μ ( a ∣ s ) \mu(a|s) μ(a∣s) 产生轨迹
- 目标策略 π ( a ∣ s ) \pi(a|s) π(a∣s) 待评估
- 在线、增量、单趟(one-pass)地估计 V π ( s ) V^\pi(s) Vπ(s) 或 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)
- 引入 eligibility trace e t e_t et 实现 多步回报 与 低方差 的平衡
汇总算法
| 符号 | 含义 |
|---|---|
| ρ t = π ( a t ∣ s t ) / μ ( a t ∣ s t ) \rho_t = \pi(a_t| s_t)/\mu(a_t | s_t) ρt=π(at∣st)/μ(at∣st) | 重要性采样比 |
| δ t I S = r t + 1 + γ V ( s t + 1 ) − V ( s t ) \delta^{IS}_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) δtIS=rt+1+γV(st+1)−V(st) | IS-TD 误差 |
| δ t P D = r t + 1 + γ ρ t + 1 V ( s t + 1 ) − V ( s t ) \delta^{PD}_t = r_{t+1} + \gamma \rho_{t+1} V(s_{t+1}) - V(s_t) δtPD=rt+1+γρt+1V(st+1)−V(st) | PD-TD 误差 |
| δ t T B = r t + 1 + γ ∑ a π ( s t + 1 , a ) V ( s t + 1 ) − V ( s t ) \delta^{TB}_t = r_{t+1} + \gamma \sum_a \pi(s_{t+1}, a) V(s_{t+1}) - V(s_t) δtTB=rt+1+γ∑aπ(st+1,a)V(st+1)−V(st) | TB-TD 误差 |
| e t ∈ R d e_t \in \mathbb{R}^d et∈Rd | eligibility trace 向量 |
| λ ∈ [ 0 , 1 ] λ \in [0,1] λ∈[0,1] | 迹衰减系数 |
| 算法 | 需要 μ 概率 | 迹权重 | 更新乘子 | 无偏条件 | 方差趋势 | 内存 |
|---|---|---|---|---|---|---|
| IS-λ | ✅ | ρ t \rho_t ρt | ρ t δ t I S e t \rho_t \delta^{IS}_te_t ρtδtISet | λ=1 | 爆炸 | O(d) |
| WIS-λ | ✅ | ρ t \rho_t ρt | ( ρ t δ t I S e t ) / M t (\rho_t \delta^{IS}_t e_t)/M_t (ρtδtISet)/Mt | 渐近 | ↓ | O(d+1) |
| PD-λ | ✅ | ρ t \rho_t ρt | δ t P D e t \delta^{PD}_t e_t δtPDet | λ=1 | 中 | O(d) |
| TB-λ | ❌ | π t \pi_t πt | δ t T B e t \delta^{TB}_t e_t δtTBet | λ=1 | 低 | O(d) |
2. Importance-Sampling Algorithms
核心思想:把整条轨迹的回报用 重要性采样比 ρ \rho ρ 加权,再用迹向量在线累积。
2.1 基本 IS
-
迹定义
- e t = γ λ ρ t e t − 1 e_t = \gamma \lambda \rho_t e_{t-1} et=γλρtet−1
-
TD error 【无 ρ \rho ρ】:
- $\delta t = r{t+1} + \gamma Q_t(s_{t+1}, a_{t+1}) - Q_t(s_t, a_t) == r_{t+1} + \gamma V_t(s_{t+1}) - V_t(s_t) $
-
更新action-value function 【有 ρ \rho ρ】:
- Q t + 1 = Q t + α ρ t δ t e t Q_{t+1} = Q_t + \alpha \rho_t \delta_t e_t Qt+1=Qt+αρtδtet
-
性质
✅ 无偏( π \pi π 下期望与 MC 一致)
❌ 方差随轨迹长度指数增长( ∏ ρ 0 : t → ∞ \prod \rho_{0:t} \rightarrow \infin ∏ρ0:t→∞)
2.2 加权 I S / W I S − λ IS / WIS-\lambda IS/WIS−λ
用 累积比重的倒数 做归一化因子,降低方差
-
在线实现需维护 加权迹
- M t = γ λ ρ t M t − 1 + 1 M_t = \gamma \lambda \rho_t M_{t-1} + 1 Mt=γλρtMt−1+1
-
更新action-value function 【有 ρ \rho ρ】:
- Q t + 1 = Q t + α ρ t δ t e t / M t Q_{t+1} = Q_t + \alpha \rho_t \delta_t e_t / M_t Qt+1=Qt+αρtδtet/Mt
-
性质
✅ 方差 ↓,仍渐近无偏
❗ 需要存储额外标量 M t M_t Mt,且对非线性逼近收敛保证弱
3. Per-Decision Importance Sampling Algorithms
动机: IS 把 整条轨迹 一起加权,方差大。
核心: Per-decision只把 当前步 ρ ρ ρ 放进 回报,而非整条轨迹;等价于 一步 IS + 多步 TD。
3.1 PD(λ) 迹
-
迹定义 与 IS 相同:(负责纠正历史特征的权重)
- e t = γ λ ρ t e t − 1 , ∀ s , a e_t = \gamma \lambda \rho_t e_{t-1}, \forall s, a et=γλρtet−1,∀s,a
-
TD error: 单步重要性采样 【有 ρ \rho ρ】:(负责纠正奖励/价值)
- δ t = r t + 1 + γ ρ t + 1 Q t ( s t + 1 , a t + 1 ) − Q t ( s t , a t ) \delta _t = r_{t+1} + \gamma \rho_{t+1} Q_t(s_{t+1}, a_{t+1}) - Q_t(s_t, a_t) δt=rt+1+γρt+1Qt(st+1,at+1)−Qt(st,at)
-
更新action-value function 【无 ρ \rho ρ】:
- Q t + 1 = Q t + α δ t e t Q_{t+1} = Q_t + \alpha \delta_t e_t Qt+1=Qt+αδtet
-
性质
- λ = 1 λ=1 λ=1 时无偏; λ < 1 λ<1 λ<1 引入 λ-加权偏差
- 方差 比 IS-λ 小一个轨迹长度因子
- 线性逼近下 收缩算子,收敛到 λ-加权 Bellman 误差 最小值
- 与 I S − λ IS-λ IS−λ 相比,方差 ↓×轨迹长度,偏差 ↑×(1-λ)。
3.2 现代技术中不用PD的原因
「裁剪 IS」= 实现简单 + 可微 + 生态成熟,而 PD-IS 的降方差优势在现代 大 batch + clip + GPU 场景下 聊胜于无,于是被生态淘汰。
工程与算法生态 发生了三点根本变化:
- 方差问题靠「裁剪/正则」解决,而非「改公式」
- IS 的 ρ² 爆炸方差确实恐怖,但 PPO、TRPO、IMPALA 等直接用 clip(ρ, 1±ε) 或 bias-corrected ρ̂ 把权重硬压到有限区间
- 方差被 人工截断 控制,同时 保持可微、易实现
- 现代流水线需要 可微、端到端
- IS 形式 ρ = π θ μ θ o l d \rho = \frac{\pi_\theta}{\mu_{\theta_{old}}} ρ=μθoldπθ 是 θ 的显式函数,可以 自动微分 穿过整个轨迹
- PD-IS 把 ρ 拆进 δ \delta δ内部,导致 δ \delta δ 也含 θ \theta θ,反向传播时要 再求一次 δ \delta δ 对 θ \theta θ 的导数,实现复杂且 Hessian 不稳
- 在大 batch + GPU 场景,「整条轨迹一次乘 ρ」 比 「每步拆 δ」 更快更内存友好
- 算法生态「以 IS 为原子」已成型
- Retrace、V-trace、IMPALA、ACER、SAC(off-policy) 都把 clip-ρ 作为 基础乐高块
- 这些高级变体 在 IS 框架内 就能达到 Bias-Variance 最优,PD-IS 的额外降方差 边际收益低
- 社区工具链(RLlib、Tianshou、Acme)默认提供 clip-ρ 算子,IS 即插即用;PD-IS 需要 重写轨迹反向逻辑,无人愿意维护
4. Tree-Backup Algorithms
核心思想:不需要 权重 μ \mu μ 的概率!用 目标策略 π \pi π 的概率 直接对回报做 加权树回溯,天生 off-policy。
4.1 Tree-Backup λ (TB-λ)
-
迹定义
- e t = γ λ π t e t − 1 e_t = \gamma \lambda \pi_t e_{t-1} et=γλπtet−1
- 定义 π \pi π-权重 π t = π ( a t ∣ s t ) \pi_t = \pi(a_t|s_t) πt=π(at∣st)
-
TD error: 单步重要性采样:(负责纠正奖励/价值)
- δ t = r t + 1 + γ ∑ a π ( s t + 1 , a ) Q t ( s t + 1 , a t + 1 ) − Q t ( s t , a t ) \delta _t = r_{t+1} + \gamma\sum_a \pi(s_{t+1}, a) Q_t(s_{t+1}, a_{t+1}) - Q_t(s_t, a_t) δt=rt+1+γ∑aπ(st+1,a)Qt(st+1,at+1)−Qt(st,at)
-
更新action-value function:
- Q t + 1 = Q t + α δ t e t Q_{t+1} = Q_t + \alpha \delta_t e_t Qt+1=Qt+αδtet
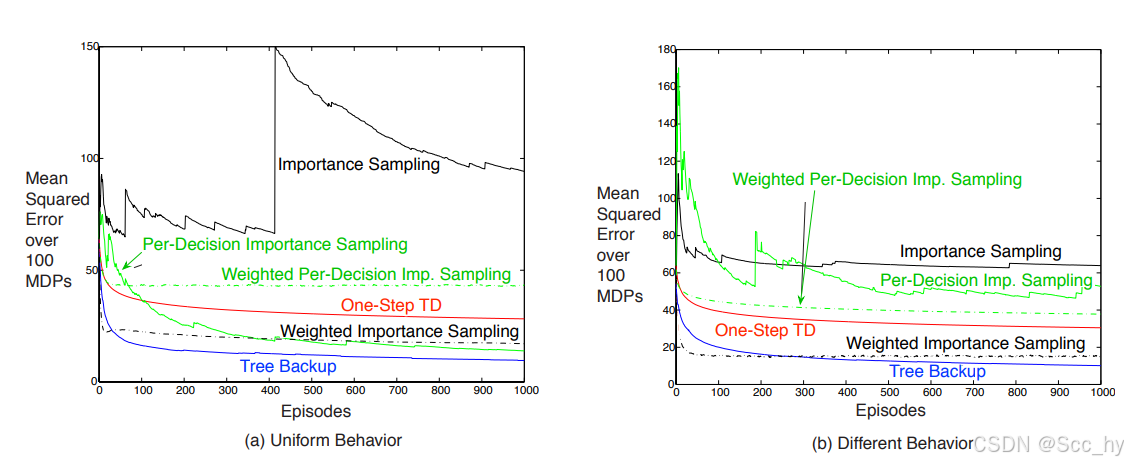
一句话总结
- IS-λ:最纯正 off-policy, ρ \rho ρ 加权整条轨迹,无偏但方差爆炸。
- PD-λ:只把当前步 ρ \rho ρ放进回报,方差 ↓,收敛保证仍在。
- TB-λ:甩掉 μ,用 π \pi π 概率做树回溯,无需行为策略概率,最适合 深度策略 + 高维动作 的 off-policy 学习。
5. Tree-Backup VS MCTS Backup
Tree-Backup 提出 “用 π \pi π 概率加权回溯” 来摆脱 μ;AlphaZero 的 MCTS Backup 正是这一思想在 完美信息博弈+深度网络 上的工程化实现,两者共享 π \pi π-加权、无 μ μ μ、低方差 的同一血统。
| 维度 | Tree-Backup λ (RL) | MCTS Backup (Planning) |
|---|---|---|
| 目的 | 在线 off-policy 策略评估 | 决策时 规划最优动作 |
| 权重来源 | π(a| s)(目标策略概率) | 访问计数 N(s,a)(UCB 驱动的频率) |
| Backup 方向 | 时间反向(沿轨迹 t→t-1→…) | 树反向(沿搜索路径 叶→根) |
| Backup 内容 | λ-加权 TD 误差 | 蒙特卡洛回报 或 神经网络估值 v_θ |
| 是否用 μ | ❌ 完全不需要行为策略 | ❌ 自对弈,μ≡π |
| 是否用 λ | ✅ 显式 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1] 控制衰减 | ❌ 隐式 λ=1(MC)或 λ=0(叶节点 bootstrap) |
| 是否在线 | ✅ 单趟轨迹即可更新 | ✅ 每仿真结束后立即 Backup |
| 数学形式 | 迹向量 e t = γ λ π t e t − 1 e_{t} = \gamma \lambda \pi_t e_{t-1} et=γλπtet−1 | Q ( s , a ) ← ( N ⋅ Q + v ) / ( N + 1 ) Q(s,a) \leftarrow (N·Q + v)/(N+1) Q(s,a)←(N⋅Q+v)/(N+1) |
| 方差控制 | π-加权,零 IS 方差 | 访问频率自动降低方差 |
MCTS Backup 可视为「λ=1 的 MC 版 Tree-Backup」在树结构上的工程化实现:二者都用 目标策略概率( π \pi π 或访问频率) 加权回溯,彻底抛弃行为策略 μ,从而天然适合 完全自对弈 的 off-policy 场景
