已知明文攻击(Known plaintext):原理、方法与防御体系深度剖析
引言:密码分析中的"半开放战场"
在加密通信的攻防博弈中,已知明文攻击(Known Plaintext Attack, KPA)是介于唯密文攻击(COA)与选择明文攻击(CPA)之间的关键攻击模型。它模拟了攻击者获取部分"明文-密文对"后的破解场景——这种场景在现实中极为常见:加密邮件的固定格式头部、物联网设备的周期性状态报告、数据库中加密字段的默认值等,都可能成为攻击者手中的"明文线索"。本文将从理论基础出发,系统解析KPA的核心原理与演进路径,深入探讨其攻击方法体系,结合经典与现代案例总结防御策略,并前瞻量子计算时代的技术挑战。
核心定义:已知明文攻击是指攻击者在掌握加密算法、一定数量的明文及其对应密文的前提下,通过分析明文与密文间的关联性,推导出加密密钥或实现未知密文破译的攻击方式。相比唯密文攻击,KPA因具备"明文参照系"大幅降低攻击难度;相比选择明文攻击,其无需主动控制明文生成,更贴合被动监听的真实攻击场景。
在密码分析的攻击模型谱系中,KPA处于承上启下的关键位置,其攻击能力直接反映加密系统对"部分信息泄露"的抵抗能力,是评估加密方案安全性的核心指标之一。
一、已知明文攻击的理论基础
1.1 攻击本质:利用明文-密文的关联性
KPA的有效性根植于加密系统的确定性与明文的结构性。从密码学基本原理看,绝大多数实用加密算法(如AES、DES)属于确定性加密——相同的明文在相同密钥和加密参数下,必然生成相同的密文。这种确定性使得明文与密文间存在固定的映射关系,而攻击者手中的"明文-密文对"正是破解这种映射关系的"钥匙"。
从信息论视角,香农提出的"唯一解距离"(Unique Decipherment Distance)概念为KPA提供了理论支撑:当攻击者获取的明文-密文对数量超过系统的唯一解距离时,加密密钥将成为唯一能解释这种映射关系的参数。例如,简单的移位密码唯一解距离仅需几十字节明文,而现代分组密码的唯一解距离则随密钥长度呈指数级增长。
1.2 攻击前提与核心假设
KPA的成功依赖两个核心前提,攻击者通常需满足以下假设:
明文样本的代表性:获取的明文需包含与未知明文相同的统计特征或结构模式(如语言规律、协议格式、数据头部等),否则关联性分析将失去意义。例如,破解英文加密文档时,若已知明文为随机字节流,即使数量再多也无法辅助攻击。
密钥与加密参数的一致性:已知明文与未知明文使用相同的密钥和加密参数(如初始化向量IV、加密模式等)。若加密系统采用一次一密或动态密钥机制,KPA将难以奏效。
算法细节的可知性:攻击者明确加密算法的具体实现(如分组密码的轮函数、流密码的密钥流生成器结构),尽管在"黑盒攻击"场景下,攻击者也可通过明文-密文对反向推断算法特征。
1.3 攻击复杂度模型
与唯密文攻击类似,KPA的复杂度同样受时间(计算资源)、空间(存储资源)、数据量(明文-密文对数量)三重因素制约。
通常情况下,增加明文-密文对的数量可显著降低计算复杂度——例如,线性分析中每多一组样本,密钥候选空间的筛选精度可提升一个数量级。这种"数据换计算"的特性,使KPA在大数据场景下(如大规模加密数据泄露)具备更强的威胁性。
二、已知明文攻击的核心方法体系
2.1 经典方法:线性分析与差分分析
线性分析与差分分析是针对分组密码的两大经典KPA方法,前者利用明文-密文对的线性关联性,后者利用非线性变换的差分特性,共同构成了现代密码分析的基础框架。
2.1.1 线性分析(Linear Cryptanalysis)
线性分析由Matsui于1993年提出,核心是寻找"明文比特线性组合→密文比特线性组合"的高概率近似关系(线性逼近式),通过大量明文-密文对验证并求解密钥。以DES为例,攻击步骤如下:
寻找线性逼近式:筛选DES轮函数中满足P⊕P⊕...≈C⊕C⊕...⊕K的线性关系,其中P为明文比特、C为密文比特、K为子密钥比特,近似概率偏离1/2越多越好。
收集样本与统计验证:获取大量明文-密文对,统计线性逼近式左右两边相等的次数,计算偏差值。
密钥求解:根据偏差值的正负性,逐步确定子密钥比特,最终组合得到完整密钥。
实验表明,对DES实施线性分析需约2组明文-密文对,计算复杂度约为2次运算,远低于暴力攻击的2。
2.1.2 差分分析(Differential Cryptanalysis)
差分分析由Biham和Shamir于1990年提出,通过分析明文对的差分(异或值)在加密过程中的传播规律,寻找高概率差分路径,进而推导出密钥。尽管差分分析常被归为选择明文攻击,但在已知明文场景下,通过筛选自然存在的差分明文对,仍可实现攻击。关键步骤包括:
构建差分路径:确定明文差分ΔP和密文差分ΔC,使得ΔP经过加密变换后以高概率变为ΔC。
筛选有效样本:从已知明文-密文对中筛选出满足ΔP的明文对及其对应密文对。
密钥推断:根据密文差分与轮函数输出的关联性,验证并确定子密钥比特。
已知明文场景下的差分分析效率低于选择明文场景(需更多样本),但对结构存在缺陷的分组密码(如早期的FEAL算法)仍具备很强的破坏力。
2.2 实用方法:模式匹配与结构化攻击
针对具备固定结构的明文(如协议帧、文件头、数据库记录),模式匹配类方法是KPA的高效实现路径,无需复杂的数学分析,直接利用明文的结构性特征定位密钥。
2.2.1 固定模式匹配攻击
当明文包含已知固定字段(如TCP报文头的"SYN"标志、PNG文件的魔法数"\x89PNG")时,攻击者可通过"密文固定字段→明文固定字段"的映射关系直接反推密钥。以流密码为例,攻击过程如下:
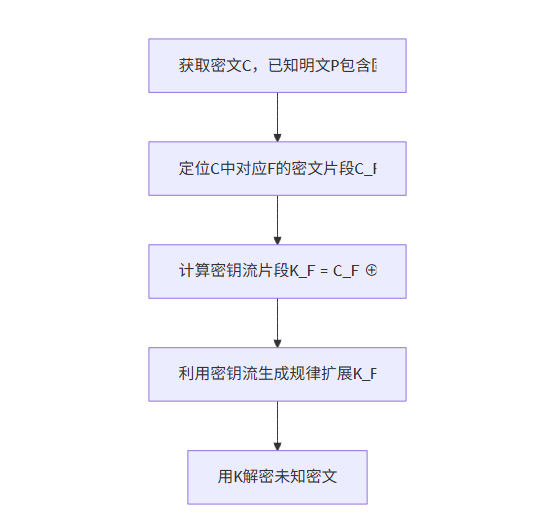
这种方法在物联网协议攻击中极为常见,例如针对LoRaWAN协议的加密攻击,攻击者可通过已知的协议控制字段(如DevAddr)推导出会话密钥。
2.2.2 滑动窗口攻击(Sliding Window Attack)
针对序列密码或分组密码的ECB模式,滑动窗口攻击通过滑动比对明文-密文对的重复模式,定位密钥长度或直接破解密钥。例如,对使用ECB模式的AES加密文件,若明文中存在重复的字节块(如连续的空格),密文中将出现相同的密文块,攻击者可通过这种重复模式:
确定分组密码的分组长度(如128位AES的重复块间隔为16字节);
关联已知明文块与密文块,建立部分密钥映射;
逐步扩展密钥映射,最终还原完整密钥。
2.3 现代方法:机器学习辅助攻击
随着人工智能技术的发展,机器学习成为KPA的新兴辅助工具,其核心优势在于自动提取明文-密文对中的非线性关联特征,突破传统方法对人工分析的依赖。典型应用包括:
密钥分类模型:使用神经网络(如CNN、RNN)将明文-密文对作为输入,密钥比特作为输出,通过大量样本训练后直接预测密钥。实验表明,对简化版AES(如AES-128的8轮实现),该方法可将攻击所需样本量降低30%。
特征提取加速:利用自编码器自动提取明文-密文对的高阶统计特征,替代传统线性分析中的人工逼近式寻找过程,效率提升约两个数量级。
黑盒算法识别:在未知加密算法的场景下,通过机器学习分类器分析明文-密文对的特征,先识别算法类型(如AES vs 3DES),再针对性选择攻击方法。
三、典型已知明文攻击案例分析
3.1 历史里程碑:DES的线性分析攻击
1994年,Matsui首次公开对DES实施线性分析攻击的完整结果,成为KPA发展史上的里程碑事件。实验条件与结果如下:
实验参数 | 具体指标 |
|---|---|
明文-密文对数量 | 2组(约8TB数据) |
计算复杂度 | 2次DES轮函数运算 |
密钥破解成功率 | 约90% |
对比暴力攻击 | 效率提升约2倍 |
该案例证明,即使是当时广泛应用的DES加密标准,在KPA场景下也存在安全漏洞,直接推动了AES等更安全加密算法的研发与普及。
3.2 现代案例:物联网LoRaWAN协议的KPA攻击
LoRaWAN是物联网常用的低功耗广域网协议,其加密机制采用AES-128,但在实际部署中因明文结构泄露存在KPA风险。攻击者利用以下条件实施攻击:
已知明文字段:LoRaWAN上行报文的DevAddr(设备地址)字段为公开信息,属于已知明文;
密文可获取:通过射频监听可获取加密后的上行报文密文;
加密模式缺陷:部分终端设备采用ECB模式加密,导致相同DevAddr对应相同密文块。
攻击步骤如下:
①监听并捕获包含DevAddr的加密报文;
②提取密文中对应DevAddr的密文块;
③计算密钥流片段K = C_DevAddr ⊕ DevAddr;
④利用AES-ECB模式的确定性,扩展密钥流破解其他字段(如传感器数据)。
2021年,某安全团队在实际测试中通过该方法,仅用5分钟就破解了某品牌智能水表的加密数据。
3.3 前沿案例:机器学习辅助的AES-128 KPA攻击
2023年,《IEEE Transactions on Information Forensics and Security》期刊发表的研究显示,利用深度学习可实现对AES-128的高效KPA。研究团队采用CNN+Transformer混合模型,核心创新点包括:
将明文-密文对转换为2D特征矩阵,保留字节间的空间关联性;
用Transformer层捕捉长距离依赖,替代传统线性分析的人工特征工程;
采用半监督学习,在少量标注样本(已知密钥)下扩展训练数据。
实验结果表明,该模型在2组明文-密文对下即可实现92%的密钥破解成功率,计算复杂度降至2,相比传统线性分析效率提升约2倍。
四、已知明文攻击的防御体系构建
4.1 算法层面:强化非线性与扩散特性
加密算法的设计需从根源上抵抗KPA的关联性分析,核心策略包括:
增强非线性变换:采用高非线性度的S盒(如AES的S盒非线性度为104),破坏明文-密文间的线性关联,使线性分析难以找到有效逼近式;
优化扩散结构:通过多轮次的行移位、列混合等操作(如AES的10轮变换),确保单个明文比特的变化扩散到所有密文比特,消除局部模式关联性;
引入随机性:采用概率加密算法(如RSA-OAEP),即使相同明文也生成不同密文,从根本上切断确定性映射关系。
4.2 协议层面:消除明文结构泄露
加密协议的设计需避免已知明文字段的可预测性,关键措施包括:
明文随机化预处理:对明文添加随机填充(如PKCS#7填充)或附加随机数前缀,破坏固定模式;例如,在加密文件时,先添加16字节随机盐值再加密,使相同文件生成不同密文;
采用安全加密模式:禁用ECB模式,选用CBC、GCM等链式加密模式,利用初始化向量(IV)的随机性打破密文块重复性;要求IV每次加密必须唯一且不可预测;
密钥动态更新:建立密钥轮换机制,根据明文-密文对的累积量动态更新密钥;例如,物联网设备每传输1000条报文后自动更换会话密钥。
4.3 实现层面:强化工程防护与审计
实际部署中的实现缺陷往往成为KPA的突破口,需通过工程手段弥补:
避免明文信息泄露:严格控制协议头部、文件头等固定字段的暴露范围,必要时对这些字段单独加密;
侧信道防护增强:即使KPA本身不依赖侧信道信息,密钥提取过程可能结合功耗、时序等泄露,需采用恒定时间算法、电磁屏蔽等防护措施;
安全审计与测试:在系统上线前,通过KPA模拟测试验证加密方案的安全性;例如,使用自动化工具生成大量明文-密文对,检测是否存在可利用的关联性。
五、挑战与未来发展方向
5.1 量子计算对KPA的影响
量子计算的发展将从两个方面重塑KPA的格局:一方面,Shor算法可加速求解线性方程组,使传统线性分析的计算复杂度从指数级降至多项式级,大幅降低攻击门槛;另一方面,量子机器学习算法(如量子支持向量机)可更高效地提取明文-密文对的非线性特征,进一步提升攻击效率。
应对这一挑战,后量子密码算法需在设计中特别强化对KPA的抵抗能力——例如,格基密码CRYSTALS-Kyber通过多项式环上的随机化操作,使明文与密文间的关联性在量子计算下仍难以捕捉。
5.2 边缘计算场景下的KPA新威胁
边缘计算设备(如智能终端、工业传感器)因资源受限,常采用轻量化加密方案,导致KPA风险升高:①轻量化算法的非线性程度较低,易被线性分析攻击;②设备存储能力有限,难以实现复杂的密钥轮换;③明文多为周期性采集的结构化数据,模式泄露风险高。
未来需研发专为边缘场景设计的抗KPA加密方案,例如基于物理不可克隆函数(PUF)的动态密钥生成技术,使每次加密的密钥与设备物理特征绑定,即使存在明文-密文对也无法推导后续密钥。
5.3 机器学习攻击的边界拓展
当前机器学习KPA仍存在两大局限:一是对完整轮数的强加密算法(如10轮AES-128)效果有限;二是需要大量标注样本(已知密钥的明文-密文对)。未来的研究方向包括:
无监督学习模型,在无密钥标注的情况下实现密钥推断;
小样本学习算法,降低对明文-密文对数量的依赖;
跨算法迁移学习,实现对未知加密算法的快速适配攻击。
结论:在关联性博弈中构建安全屏障
已知明文攻击的本质是对"明文-密文关联性"的挖掘与利用,其发展历程反映了密码学从"绝对安全"向"计算安全"再到"工程安全"的演进逻辑。从DES的线性分析到机器学习辅助的AES攻击,攻击者的手段不断突破,但防御技术也在同步升级——非线性变换增强、概率加密、动态密钥管理等策略,共同构建起抵御KPA的多层防线。
未来,随着量子计算与人工智能的深度融合,KPA的攻防博弈将进入新的阶段。对密码学研究者而言,需在理论层面探索抗量子KPA的新范式;对工程实践者而言,需严格落实加密标准,避免因实现缺陷给攻击者留下可乘之机。只有将理论严谨性与工程安全性紧密结合,才能在已知明文攻击的"半开放战场"上构筑起真正可靠的信息安全屏障。
