算法入门数学基础

目录

 例题1：辗转相除法（欧几里得算法）

例题2：n的n次方求个位

例题3：斐波那契规律题

例题4：快速幂

快速幂的模版：

例题5：二分查找

二分查找模版：

例题6： 二分的应用

例题7：三分查找

---

本章重点：

• 欧几里得算法
• 找规律
• 快速幂运算
• 二分查找
• 三分查找

导引问题：整数求和

任务：给定一个正整数n，计算1+2+3+....+n的结果，其中n  <= 50000。

代码1：使用循环累加

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int main() {int n = 0;int sum = 0;scanf("%d", &n);int i = 0;for (i = 0; i <= n; i++) {sum += i;}printf("%d\n", sum);return 0;
}

方法2：使用高斯公式：n +（n+ 1） / 2

        那么问题来了，我们知道题目的范围n  <= 50000。如果这里我们假设n = 50000。如果使用高斯公式50000 * 50001 = 2,500,050,000超过了int类型。这里就需要使用long long。那么可以不使用long long 来计算吗？

        解决方案1：使用long long。%lld 8字节64bit。

        解决方案2：先除后乘 这里要考虑奇偶性，做一个判断。     

 例题1：辗转相除法（欧几里得算法）

任务：给定两个正整数，计算这两个数的最小公倍数（能同时被两个数整除的最小数）。

样例输入：

10 14 

4 6

样例输出：

70 

12

方法1：暴力枚举

方法2：从大数开始枚举大数的倍数（枚举的改进）。

方法3：辗转相除法。

公式：LCM(A,B) = A * B / GCD(A, B)

上面公式解释A 和 B 的最小公倍数 = A * B / （A和B的最大公约数）。

注意：上面公式可以会出现导引中提到过的一个问题 int 类型可能会爆。所以也要进行转换先除后乘， 或者使用long long类型。

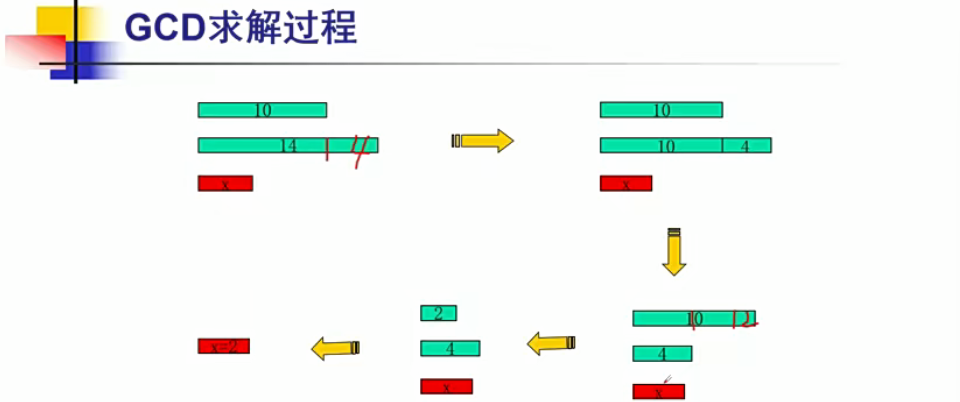
这里以10 和 14 作为例子进行说明求解过程：具体过程看上图。

#include<stdio.h>//辗转相除法求gcd
int gcd(int da, int xiao) {int tep;while (xiao != 0) {tep = da % xiao;da = xiao;xiao = tep;}return da;
}int main() {//求a和b的最小公倍数int a = 14;int b = 10;int ans = a / gcd(a, b)*b;printf("%d \n", ans);return 0;
}

思考：大小两个参数位置是否可以变？答案可以，循环一次就能纠正过来，多做一次循环。

例题2：n的n次方求个位

任务：给定一个整数N，请计算N个N相乘的结果的个位数是都少（1 <= N <= 1000）。

方法1：暴力。这显然是不行的原因N的N次方太大了long long类型都不能放下。

方法2：做n - 1趟循环每次都取出个位数。为什么只取出个位就可以？原因：因为结果要的是个位所以其他位的不会影响个位的结果。

#include<stdio.h>int main() {int N = 0;scanf("%d", &N);int i = 0;int ans = N;for (i = 0; i < N - 1; i++) {ans =  N * ans;ans = ans % 10;}printf("%d", ans);return 0;
}

方法3：抽屉原理，找规律。因为个位数只能有10种情况。在很多题目中会出现循环节。

        抽屉原理：桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。

例题3：斐波那契规律题

        有一种fibonacci数列，定义如下：F(0) = 7,F(1) = 11, F(n) = F(n - 1) + F(n - 2)  (n >= 2)。给定一个n（n <= 1 000 000）,请判断F(n)能否被3整除，分别输出yes和no。

分析这里的n太大了暴力绝对不可行。那么怎么去考虑呢？

改良暴力：通过上面的地推式推出：F(n) % 3 = （F(n - 1) % 3 + F(n - 2)  % 3） % 3

打表找规律：

#include<stdio.h>int main() {//int arr[100];//arr[0] = 7 % 3;//arr[1] = 11 % 3;//int i = 0;////for (i = 2; i < 100; i++) {//	int ant = (arr[i - 1] % 3 + arr[i - 2] % 3) % 3;//	arr[i] = ant;//}//for (i = 0; i < 100; i++) {//	printf("%d ", arr[i]);//}//通过打表没8个为一个循环节//1 2 0 2 2 1 0 1 //3 7int N;scanf("%d", &N);if ((N % 8) == 3 || (N % 8) == 7) {printf("%s\n", "yes");}else {printf("no");}return 0;
}

例题4：快速幂

任务：求A^B的最后三位数表示的整数（1 <= A, B <= 10000）。

样例输入：

2 3

12 6

样例输出：

8

984

方法1：直接暴力； 出现的问题数据太大可能会使int 或者long long爆掉。

方法2：改进的暴力。这里的A， B都小于10000可以使用暴力。如果数据更大该怎么办，看方法3。

#include<stdio.h>int main() {int A;int B;scanf("%d %d", &A, &B);int ans = 1;int i = 0;for (i = 0; i < B; i++) {ans *= A;ans %= 1000;  //题目只要最后三位数}printf("%d\n", ans);return 0;
}

方法3：快速幂

        顾名思义，快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高。

        快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。        

快速幂的模版：

// 快速幂模版递归方式
int power(int a, int n) {int ans;if (n == 0) {ans = 1;}else {ans = power(a * a, n / 2);if (n % 2 == 1) {ans *= a;}}return ans;
}//快速幂非递归方法
int power(int a, int n) {int ans = 1;while (n) {if (n % 2==1) {ans = ans * a;}a = a * a;n /= 2;}return ans;
}

快速幂模版取模版本：

        取模的原因：是因为A^N次方一般特别大在算法题出现类似的题一般会取模。下面代码是对1000取模。

// 快速幂模版递归方式
int power(int a, int n) {int ans;if (n == 0) {ans = 1;}else {ans = power((a * a) % 1000, n / 2);if (n % 2 == 1) {ans =(ans * a % 1000);}}return ans;
}//快速幂非递归方法
int power(int a, int n) {int ans = 1;while (n) {if (n % 2==1) {ans = (ans * a) % 1000;}a = (a * a) % 1000;n /= 2;}return ans;
}

例题5：二分查找

        给出若干个（可以很多）有序的整数，请查找某个元素是否存在，比如在1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20中查找15。如果找到返回元素的下标，找不到返回-1。

注意：二分查找的前提是——数据是有序的。

        二分法搜索（Binary Search），又称折半搜索、对数搜索，是一种在有序数组中查找特定元素的搜索算法 。该算法时间复杂度为O(log n)，迭代实现空间复杂度为O(1)，递归实现则为O(log n)。

二分查找模版：

非递归模版

//二分查找模版
int BiSearch(int a[], int n, int x) {/*arr数组 * n是数组的长度* x所要查找的数值*/int left = 0;int right = n - 1;while (left <= right) {				//注意：这里等号不能少int mid = (left + right) / 2;   //整数除法if (a[mid] == x) {				//找到的情况return mid;}if (x > a[mid]) {				//如果比查找的值大left = mid + 1;}else {right = mid - 1;			//如果比查找的值小}}return -1;  //没有找到返回-1
}

递归模版：

  写递归时候一般先写递归出口

//二分查找模版
int BiSearch(int a[], int x, int left, int right) {/*a数组 * x所要查找的数值*/if (left > right) {//递归出口return -1;}else {int mid = (left + right) / 2;if (a[mid] == x)return mid;else if (x > a[mid])return BiSearch(a, x, mid + 1, right);elsereturn BiSearch(a, x, left, mid - 1);}
}

思考：在一百万个有序元素中用二分查找一个元素大约需要比较多少次？

答案：大约20次。

时间复杂度：O(logN)。

例题6： 二分的应用

        给出方程：其中，实数Y满足（fabs（Y）<= 1e10）请输出x的区间[0, 100]的解，精确到小数点后4位。（输入Y求x）

#include<stdio.h>
double f(double x){//题目中的式子return 8 * x*x*x*x + 7 * x*x*x + 2 * x*x + 3 * x + 6;
}
int main() {double Y;double left, right, mid;int t;scanf("%d", &t);//测试次数while (t--) {scanf("%lf", &Y);if (f(0) <= Y && Y <= f(100)) {left = 0;right = 100;while (right - left > 1e-6) {mid = (left + right) / 2;double ans = f(mid);if (ans > Y)right = mid - 1e-7;elseleft = mid + 1e-7;}printf("%.4f\n", (left + right) / 2);}elseprintf("No solution!\n");//没找到符合的结果}return 0;
}

例题7：三分查找

        给定函数：其中，实数y满足（0 < y < 1e10）请输入x在区间[0, 100]时函数F(x)的最小值，结果精确到小数点后4位。（输入y求x）

方法1：求导找到倒数为0的点就是最小值

方法2：三分查找

        三分查找（Ternary Search）是一种用于在单峰函数（凸函数或凹函数）上高效逼近最大值或最小值的搜索算法，通过每次迭代将搜索区间三等分并排除无效部分，时间复杂度为O(log₃n)

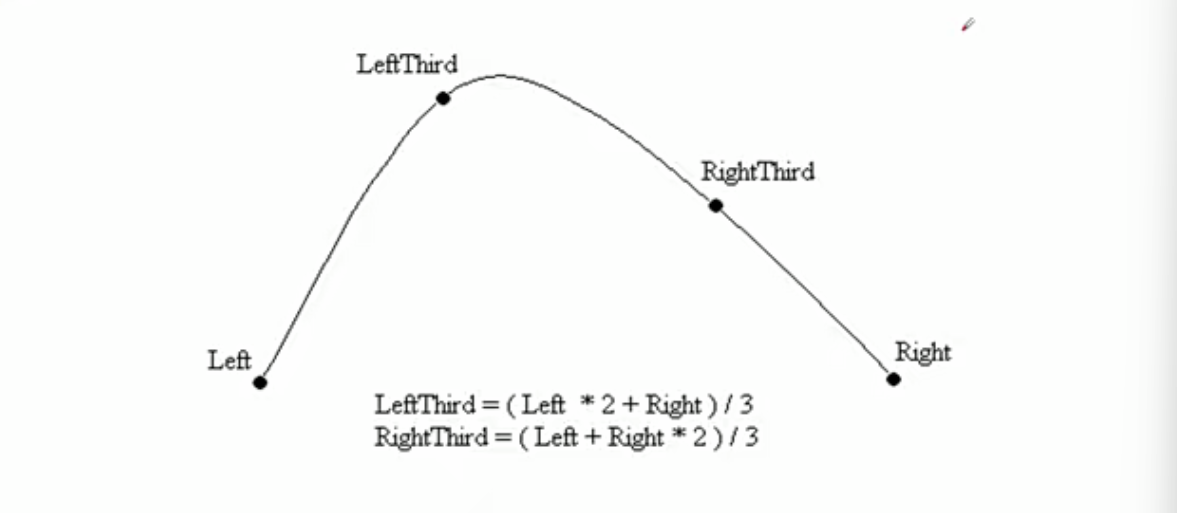
         三分查找：用来求极值点，和二分查找不同，二分查找比较的是所查找的值是否等于下标为mid元素的值，而三分查找比较的是LeftThird 和 RigthThird的Y值。

        总结：二分查找要求单调性。

                    三分的前提------数据的凸凹性，这里的凸凹不要求单调。

非递归

#include <stdio.h>
#include <math.h>
double pow(double a, int n) {double ans = 1;for (int i = 0; i < n; i++) {ans *= a;}return ans;
}double f(double x, double y) {return 6 * pow(x, 7) + 8 * pow(x, 6) +7 * pow(x, 3) + 5 * pow(x, 2) - y * x;
}
int main() {double y;scanf("%lf", &y);double left = 0;double right = 100;//这里的循环结束标志是两个数的f函数的绝对值小于1e-7，因为要求保留4位小数double epsilon = 1e-7;while (fabs(right - left) > epsilon) {double leftThird = left + (right - left) / 3;double rightThird = right - (right - left) / 3;if (f(leftThird, y) < f(rightThird, y)) {right = rightThird - epsilon;
//这里是不需要考虑偏移的，原因是因为循环结束条件是绝对值小于1e-7，如果left == right也不会死循环}else {left = leftThird + epsilon;}}printf("%.4lf", f((left + right) / 2, y));return 0;
}

递归

#include <stdio.h>
#include <math.h>double pow(double a, int n) {double ans = 1;for (int i = 0; i < n; i++) {ans *= a;}return ans;
}double f(double x, double y) {return 6 * pow(x, 7) + 8 * pow(x, 6) +7 * pow(x, 3) + 5 * pow(x, 2) - y * x;
}double san(double y, double left, double right) {double epsilon = 1e-7;if (fabs(right - left) < epsilon) {return f((left + right) / 2, y);}double leftThird = left + (right - left) / 3;double rightThird = right - (right - left) / 3;if (f(leftThird, y) < f(rightThird, y)) {return san(y, left, rightThird - epsilon);}else {return san(y, leftThird + epsilon, right);}
}int main() {double y;scanf("%lf", &y);double left = 0;double right = 100;double ans = san(y, left, right);printf("%.4lf", ans);return 0;
}