数据结构与算法(递归)
递归的定义
“从前有座山,山里有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,讲的是什么呢?从前有座山,山里有座庙,庙里有个老和尚,老和尚在给小和尚讲故事……” 大家仔细想想,这个故事有什么特别之处? 其实,它在不断地重复自身,故事里的老和尚讲的故事和开头的故事是一样的,就像是在一个故事内部又包含了一个完全相同的 “子故事”。而我们今天要学习的 “递归”,其核心思想和这个故事有着异曲同工之妙。

- 递归:在定义一个过程或函数时出现调用本过程或本函数的成分,称之为递归。
- 若调用自身,称之为直接递归。
- 若过程或函数p调用过程或函数q,而q又调用p,称之为间接递归。
- 如果一个递归过程或递归函数中递归调用语句是最后一条执行语句,则称这种递归调用为尾递归。
例:以下是求n!(n为正整数)的递归函数。int fun(int n){ if(n==1) //语句1 return 1; //语句2 else //语句3 return fun(n-1)*n; //语句4 }
解析:在该函数fun(n)求解过程中,直接调用fun(n-1)(语句4)自身,所以它是一个直接递归函数。又由于递归调用是最后一条语句,所以它又属于尾递归
递归模型是递归算法的抽象,它反映一个递归问题的递归结构。一般情况下,一个递归模型由递归出口和递归体两部分组成。
递归出口确定递归到何时结束,即指出明确的递归结束条件。
递归体确定递归求解时的递推关系。
例如,求n!的递归算法对应的递归模型如下:
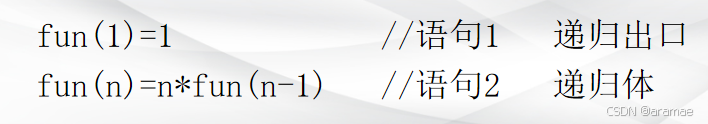
模型中,语句1给出了递归的终止条件是递归的出口,
语句2给出了函数 fun(n)的值与函数fun(n-1)的值之间的关系是递归体。
以下三种情况常常要用到递归的方法:
- 定义是递归的
- 数据结构是递归的
- 问题的求解方法是递归的
有许多数学公式、数列等的定义是递归的。
例如,求n!和Fibonacci数列(菲波那切数列)等。
这些问题的求解过程可以将其递归定义直接转化为对应的递归算法
有些数据结构是递归的。例如, 单链表就是一种递归数据结构,其结点类型定义如下:
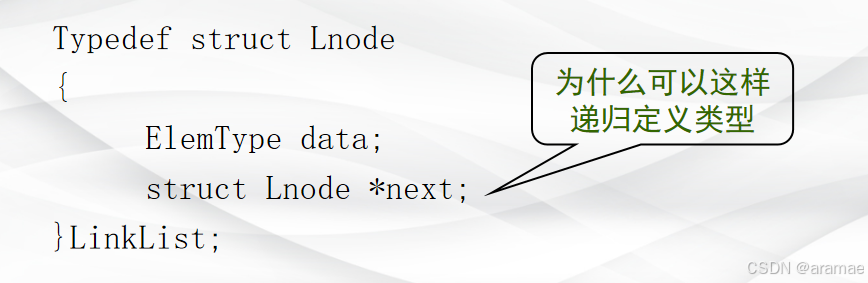
该定义中,结构体LNode的定义中用到了它自身,即指针域next 是一种指向自身类型的指针,所以它是一种递归数据结构。
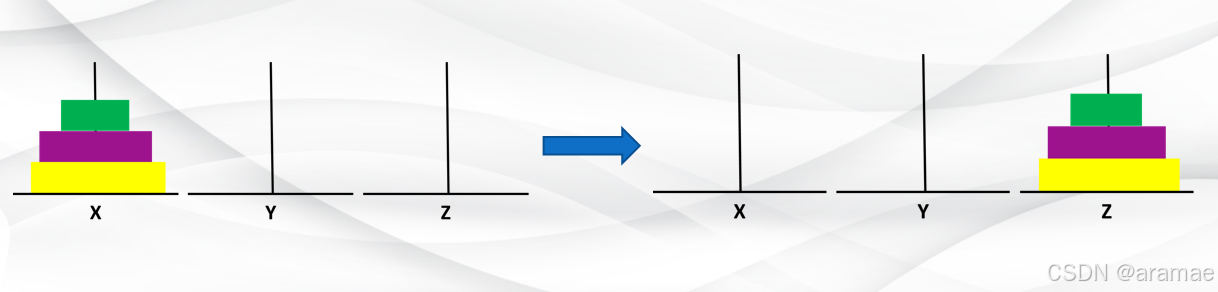
有些问题的解法是递归的,例如Hanoi问题求解。
Hanoi问题描述是:设有3个分别命名为X,Y和Z的塔座,在塔座X上有n个直径各不相同,从小到大依次编号为1,2,…,n的盘片,现要求将X塔座上的n个盘片移到塔座Z上并仍按同样顺序叠放。
盘片移动时必须遵守以下规则:
1. 每次只能移动一个盘片;
2. 盘片可以插在X、Y和Z中任一塔座;
3. 任何时候都不能将一个较大的盘片放在较小的盘片上。
设计递归求解算法,将其转换为非递归算法。
汉诺塔问题算法:void Hanoil(int n,char X,char Y,char Z)
{if(n==1)printf(“将第%d个盘子从%c移到%c。”,n,X,Z);else{Hanoil(n-1,X,Z,Y);printf(“将第%d个盘子从%c移到%c。”,n,X,Z);Hanoil(n-1,Y,X,Z);}
}
递归与数学归纳法
递归是算法和程序设计的一种实现技术。
数学归纳法是一种论证方法。
数学归纳法是递归求解问题的理论基础。递归的思想来自数学归纳法。

