「深度学习笔记2」线性代数——深度学习的“骨架”

1. 线性代数是什么？

线性代数是数学的一个重要分支，主要研究向量、矩阵、线性方程组和线性变换等概念。如果把深度学习比作一栋高楼，那么线性代数就是这栋高楼的"钢筋骨架"——它虽然不直接可见，却支撑着整个建筑的结构稳定性。

1.1 基本数学对象

在深度学习中，数据通常以以下几种形式表示：

• 标量(Scalar)：单个数字，比如温度值25℃或者商品价格99.5元
• 向量(Vector)：一维数组，比如一个学生的各科成绩 [数学90, 英语85, 物理88]
• 矩阵(Matrix)：二维表格，比如全班学生的成绩单：

    | 数学 | 英语 | 物理 |
张三 |  90  |  85  |  88  |
李四 |  78  |  92  |  85  |

• 张量(Tensor)：多维数组，这是深度学习中最常用的数据结构，比如多个班级多个科目的成绩表（3维)

1.2 为什么线性代数对深度学习如此重要？

深度学习本质上是大规模的数据变换和特征提取，而这些操作几乎都是通过矩阵运算完成的。举个例子，在神经网络中，每一层都可以看作是一个线性变换（加上非线性激活函数）：输入数据与权重矩阵相乘，加上偏置向量，得到输出结果。这种矩阵运算可以高度并行化，这正是GPU能够加速深度学习训练的原因。

2. 核心概念与运算详解

2.1 矩阵运算及其几何意义

矩阵加法/减法

对应位置元素相加或相减，就像合并两份成绩单后计算总分或差异。从几何角度看，矩阵加法相当于向量的平移变换。

矩阵乘法：深度学习的核心运算

矩阵乘法是深度学习中最常见且最重要的运算。例如，在一个简单的神经网络层中：

输出 = 输入 × 权重矩阵 + 偏置

或者用数学公式表示：y = Wx + b

其中W是权重矩阵，x是输入向量，b是偏置向量。这种矩阵乘法允许我们同时处理大量数据，极大提高了计算效率。

矩阵转置

将矩阵的行列互换，类似于把横着的表格竖过来看。在深度学习中，转置常用于确保矩阵维度匹配，以便进行乘法运算。

表1：基本矩阵运算及其在深度学习中的应用

运算类型	数学表示	几何意义	深度学习应用
矩阵加法	A + B	平移变换	偏置项的添加
矩阵乘法	A × B	线性变换	神经网络前向传播
矩阵转置	Aᵀ	轴交换	维度调整，梯度计算

2.2 行列式：衡量线性变换的"缩放因子"

行列式是方阵的一个标量值，可以判断矩阵是否可逆。从几何角度看，行列式的绝对值表示线性变换后面积或体积的缩放比例，符号表示方向是否改变。

• 行列式为0：表示矩阵不可逆，变换后维度降低（如从平面压缩到直线）
• 行列式为1：保持面积/体积不变的变换（如旋转）

2.3 范数：度量向量"大小"的尺子

范数用于衡量向量的"大小"或"长度"，在深度学习中常用于正则化，防止模型过拟合：

L1 范数（曼哈顿范数）

• 定义：向量所有分量绝对值的和。
• 公式： $\Vert \mathbf{x}{\Vert }_1={\sum }_{i=1}^n|x_i|$
• 例子：向量 [3, 4] 的 L1 范数 = |3| + |4| = 7。
• 几何意义：在二维平面上，像是从点(0,0)走到点(3,4)的“曼哈顿距离”（只能沿网格走），总路程是7。
• 主要用途：在机器学习中用于L1正则化（Lasso正则化），它可以产生稀疏模型，即让不重要的特征权重变为0，从而实现特征选择。

L2 范数（欧几里得范数）

• 定义：向量各分量平方和再开根号。这是最直观的“长度”概念。
• 公式：$\Vert \mathbf{x}{\Vert }_2=\sqrt{{\sum }_{i=1}^n{x}_i^2}$
• 例子：向量 [3, 4] 的 L2 范数 = $\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$。
• 几何意义：就是空间中两点之间的直线距离。
• 主要用途：最常用的范数。在机器学习中用于L2正则化（岭回归），它通过惩罚较大的权重来防止过拟合，但通常不会将权重恰好降为0。

L∞ 范数（最大范数）

• 定义：向量所有分量绝对值的最大值。
• 公式：$\Vert \mathbf{x}{\Vert }_{\infty }=\max (|x_1|,|x_2|,...,|x_n|)$
• 例子：向量 [3, 4] 的 L∞ 范数 = max(|3|, |4|) = 4。
• 几何意义：衡量的是向量在任意坐标轴方向上的最大变化量。
• 主要用途：在某些工程和数学领域，当系统的性能由最大误差决定时，会使用此范数。

3. 线性方程组：深度学习中的"应用题"

线性方程组的一般形式是 Ax = b，其中：

• A是系数矩阵（如各科成绩的权重）
• x是未知数向量（如各科得分）
• b是结果向量（如总分）

3.1 解的存在性与唯一性

根据线性代数理论，方程组解的情况有以下几种：

1. 有唯一解：当A是满秩方阵时，存在唯一解 x = A⁻¹b
2. 有无穷多解：当方程数少于未知数时（欠定系统）
3. 无解：当方程之间存在矛盾时（超定系统）

在深度学习中，我们经常遇到超定系统（方程数多于未知数），这时我们寻找最小二乘解，即最小化 ||Ax - b||²，这正好是线性回归和神经网络的基础。

3.2 实际应用案例：房价预测

假设我们想根据房屋面积、卧室数量和地理位置预测房价。我们可以建立如下线性模型：

房价 = w₁ × 面积 + w₂ × 卧室数 + w₃ × 位置评分 + b

收集多组房屋数据后，我们可以构建线性方程组，并用矩阵形式表示为 y = Xw，其中X是特征矩阵，w是权重向量，y是房价向量。

4. 线性变换：深度学习的"灵魂"

4.1 什么是线性变换？

数学定义：
对于任意向量 $\mathbf{u}$, $\mathbf{v}$ 和标量 $c$，变换 $T$ 是线性的当且仅当满足：

1. 可加性：$T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})$
2. 齐次性：$T(c\mathbf{u})=cT(\mathbf{u})$

简单例子：
假设有一个线性变换 $T$，其对应的矩阵为：
$$A=\left[\begin{array}{cc}2& 0\\ 0& 3\end{array}\right]$$
对向量 $\mathbf{v}=[1,2]$ 进行变换：
$$T(\mathbf{v})=A\cdot \mathbf{v}=\left[\begin{array}{cc}2& 0\\ 0& 3\end{array}\right]\cdot \left[\begin{array}{c}1\\ 2\end{array}\right]=\left[\begin{array}{c}2\times 1+0\times 2\\ 0\times 1+3\times 2\end{array}\right]=\left[\begin{array}{c}2\\ 6\end{array}\right]$$
这就是一个简单的缩放变换：x方向放大2倍，y方向放大3倍。

在深度学习中，神经网络的每一层都在进行这样的线性变换：输出 = 权重矩阵 · 输入 + 偏置。

4.2 特征值与特征向量：揭示变换的本质

数学定义：
对于矩阵 $A$，如果存在非零向量 $\mathbf{v}$ 和标量 $\lambda$，使得：
$$A\cdot \mathbf{v}=\lambda \mathbf{v}$$
则称 $\mathbf{v}$ 是 $A$ 的特征向量，$\lambda$ 是对应的特征值。

简单例子：
考虑矩阵 $A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$
求解特征值：$\det (A-\lambda I)=0$
$$\left|\begin{array}{cc}2-\lambda & 1\\ 1& 2-\lambda \end{array}\right|=(2-\lambda {)}^2-1={\lambda }^2-4\lambda +3=0$$
解得特征值：${\lambda }_1=3$, ${\lambda }_2=1$

对 ${\lambda }_1=3$，求特征向量：
$$\left[\begin{array}{cc}2-3& 1\\ 1& 2-3\end{array}\right]\cdot \mathbf{v}=\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right]\cdot \mathbf{v}=0$$
解得 ${\mathbf{v}}_1=[1,1]$ （方向不变，长度变为3倍）

对 ${\lambda }_2=1$，求特征向量：
$$\left[\begin{array}{cc}2-1& 1\\ 1& 2-1\end{array}\right]\cdot \mathbf{v}=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\cdot \mathbf{v}=0$$
解得 ${\mathbf{v}}_2=[1,-1]$ （方向不变，长度不变）

在深度学习中，特征值分析有助于理解模型的稳定性和优化过程。例如，梯度下降法的收敛速度与Hessian矩阵的特征值分布密切相关。

4.3 在深度学习中的关键应用

优化过程中的重要性：
梯度下降法的收敛速度确实与Hessian矩阵的特征值分布密切相关。损失函数 $L$ 在点 $\mathbf{w}$ 的Hessian矩阵 $H$ 包含二阶导数信息：
$$H=\left[\begin{array}{ccc}\frac{{\partial }^{2}L}{\partial w_1^2}& \frac{{\partial }^{2}L}{\partial w_1\partial w_2}& \cdots \\ \frac{{\partial }^{2}L}{\partial w_2\partial w_1}& \frac{{\partial }^{2}L}{\partial w_2^2}& \cdots \\ ⋮& ⋮& \ddots \end{array}\right]$$

收敛性分析：
学习率 $\eta$ 的选择与最大特征值 ${\lambda }_{\max }$ 相关，需要满足：
$$\eta <\frac{2}{{\lambda }_{\max }}$$
才能保证梯度下降法的收敛性。

条件数的影响：
条件数 $\kappa =\frac{{\lambda }_{\max }}{{\lambda }_{\min }}$ 决定了优化问题的难度：

• $\kappa \approx 1$：容易优化（各方向曲率相似）
• $\kappa \gg 1$：难以优化（需要谨慎选择学习率）

这种特征值分析帮助我们理解为什么某些神经网络结构更难训练，也为改进优化算法提供了理论基础。

通过理解线性变换和特征分析，我们能够更深入地洞察深度学习模型的行为和性能特征，为模型设计和优化提供理论指导。

5. 实际案例：用Python实现线性代数运算

5.1 解线性方程组

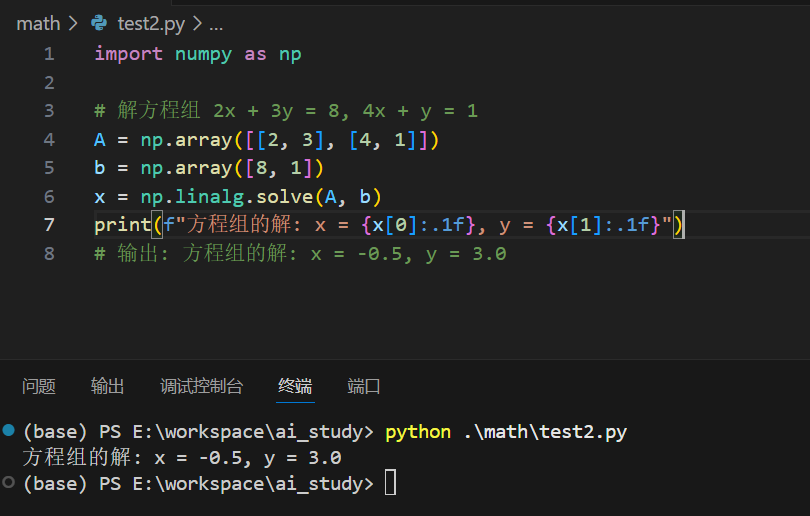
5.2 矩阵乘法模拟神经网络层

# 模拟一个简单的神经网络层
input_size = 3
hidden_size = 4
batch_size = 2# 随机生成输入数据和权重矩阵
X = np.random.randn(batch_size, input_size)  # 输入矩阵
W = np.random.randn(input_size, hidden_size)  # 权重矩阵
b = np.random.randn(hidden_size)  # 偏置向量# 前向传播计算
Z = np.dot(X, W) + b  # 线性变换
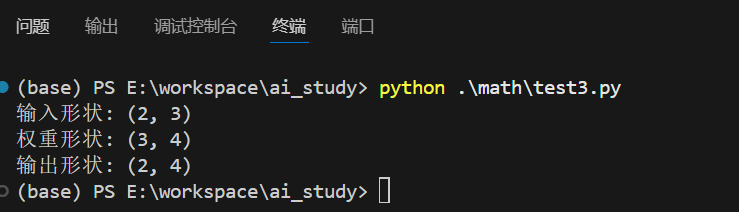
print("输入形状:", X.shape)
print("权重形状:", W.shape)
print("输出形状:", Z.shape)

运行结果:

5.3 特征值分解

# 对称矩阵的特征值分解
A = np.array([[2, 1], [1, 2]])
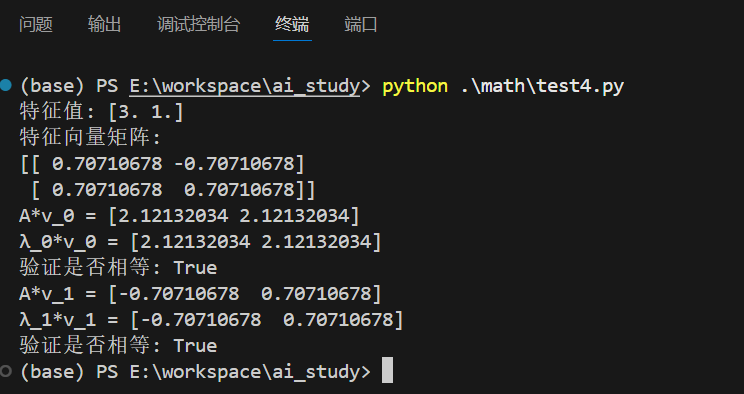
eigenvalues, eigenvectors = np.linalg.eig(A)print("特征值:", eigenvalues)
print("特征向量矩阵:")
print(eigenvectors)# 验证特征值定义: A*v = λ*v
for i in range(len(eigenvalues)):v = eigenvectors[:, i]λ = eigenvalues[i]print(f"A*v_{i} = {np.dot(A, v)}")print(f"λ_{i}*v_{i} = {λ*v}")print("验证是否相等:", np.allclose(np.dot(A, v), λ*v))

运行结果:

6. 线性代数在深度学习中的具体应用

6.1 卷积神经网络(CNN)中的卷积运算

卷积操作本质上是矩阵的局部乘法。在图像处理中，卷积核（一个小矩阵）在输入图像上滑动，进行局部矩阵乘法，提取特征如边缘、纹理等。

6.2 自注意力机制(Self-Attention)

Transformer模型中的自注意力机制核心是矩阵乘法：

Attention(Q, K, V) = softmax(QKᵀ/√d_k)V

其中Q(查询)、K(键)、V(值)都是通过输入向量与权重矩阵相乘得到的。这种机制允许模型关注输入中不同部分的重要性。

6.3 主成分分析(PCA)用于降维

PCA通过特征值分解寻找数据中方差最大的方向，用于高维数据可视化、去噪和特征提取：

1. 计算数据协方差矩阵
2. 特征值分解找到主成分
3. 投影到主成分空间实现降维

7. 总结

线性代数是深度学习的基础语言和核心工具。从简单的矩阵乘法到复杂的特征值分解，线性代数为理解和实现深度学习模型提供了必要的数学框架。

通过本文的介绍，希望你能认识到线性代数不是一堆枯燥的公式，而是理解数据变换和特征提取的强大工具。掌握线性代数，不仅能帮助你更深入理解深度学习原理，还能为学习更高级的机器学习算法打下坚实基础。