优先级队列的学习
优先级队列
队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,这种场景下,使用队列显然不合适。比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话;初中那会班主任排座位时可能会让成绩好的同学先挑座位。
在这种情况下,数据结构应该提供两个最基本的操作**,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列**(PriorityQueue)。
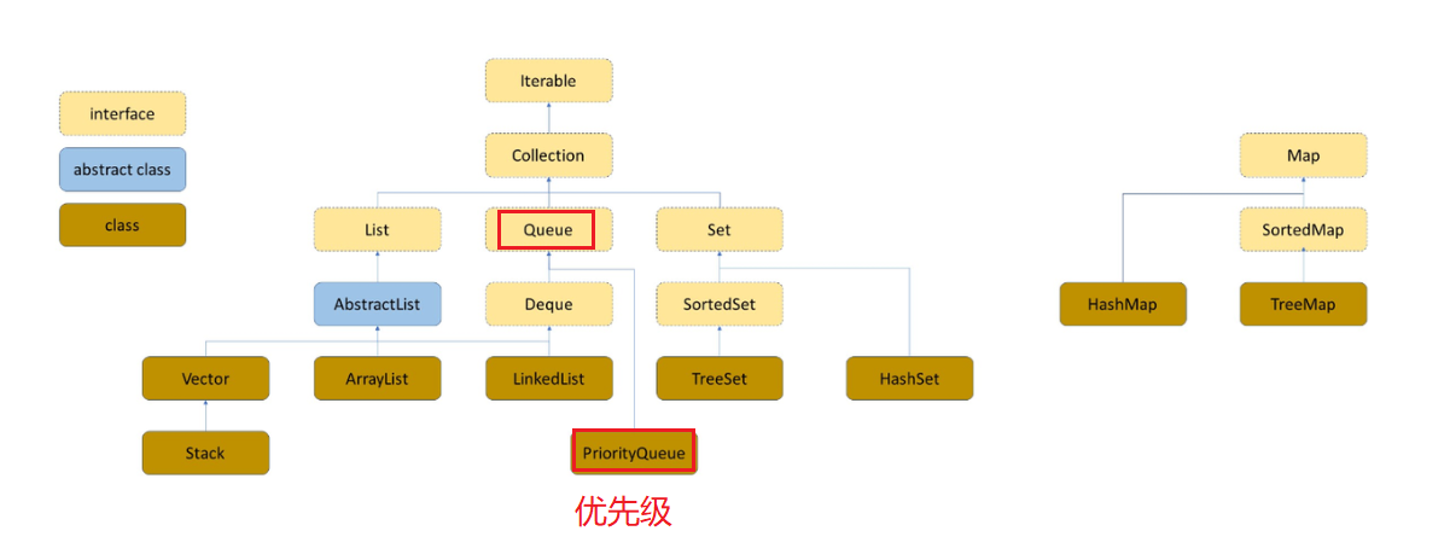
优先级队列的模拟实现
JDK1.8 中的 PriorityQueue 底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
如果有一个关键码的集合 K={k₀,k₁,k₂,…,kₙ₋₁},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Kᵢ≤K₂ᵢ₊₁ 且 Kᵢ≤K₂ᵢ₊₂(或 Kᵢ≥K₂ᵢ₊₁ 且 Kᵢ≥K₂ᵢ₊₂)(i=0,1,2…),则称为小堆(或大堆)。
其中,根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
这种定义体现了堆的核心特性:堆是完全二叉树的顺序存储结构,且父节点与子节点之间存在严格的大小关系(小堆中父节点小于等于子节点,大堆中父节点大于等于子节点),这也是堆能高效支持优先级队列操作的基础。
堆的性质:
• 堆中某个节点的值总是不⼤于或不⼩于其⽗节点的值;
• 堆总是⼀棵完全⼆叉树,分为大根堆和小根堆
堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以按层序的规则采用顺序的方式来高效存储。
左边这一张图适合用数组去存,因为他是完全二叉树,每一个都有位置
右边这一张图不适合可以用数组去存,为了能还原二叉树,空间中必须要存储空字节点,一些空间是null也被占用,导致空间来利用率比较低。
将元素存储到数组中后:
- 如果 i 为 0,则 i 表示的节点为根节点,否则 i 节点的双亲节点为 (i-1)/2
- 如果 2i+1 小于节点个数,则节点 i 的左孩子下标为 2i+1(即左孩子存在,不超出数组范围)。,否则没有左孩子
- 如果 2i+2 小于节点个数,则节点 i 的右孩子下标为 2i+2,(即右孩子存在,不超出数组范围)。否则没有右孩子
堆的创建
堆向下调整
向下调整过程(以小堆为例):
让 parent 标记需要调整的节点,child 标记 parent 的左孩子(注意:parent 如果有孩子,一定先是有左孩子)。
如果 parent 的左孩子存在,即:child < size,进行以下操作,直到 parent 的左孩子不存在:
检查 parent 的右孩子是否存在,若存在则找到左右孩子中最小的孩子,让 child 标记这个最小的孩子。
将 parent 与较小的孩子 child 比较:
若 parent 小于较小的孩子 child,调整结束。
否则:交换 parent 与较小的孩子 child。交换完成后,parent 中较大的元素向下移动,可能导致子树不满足堆的性质,因此需要继续向下调整,即 parent = child;child = parent * 2 + 1;然后重复步骤 2。

usedSize 表示实际有效节点数
- len 是数组的总容量(数组长度),即数组最多能存储的节点数。
- usedSize 是当前已存储的有效节点数量(0 ≤ usedSize ≤ len)。
- usedSize - 1 表示最后一个有效节点的索引(因为数组下标从 0 开始)。
usedSize - 1 < len(因为 usedSize ≤ len,当 usedSize = len 时,usedSize - 1 = len - 1,等于数组最大索引)。 - 当然某些场景中,usedSize 可能直接表示数组长度(即所有数组元素都是有效节点),此时 usedSize = len。
createHeap 方法:堆的构建入口
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {siftDown(parent, usedSize);
}
- 从最后一棵子树的根节点开始(通过 (usedSize-1-1)/2 计算父节点下标),从下往上、从右往左遍历每一棵子树。
- 对每棵子树调用 siftDown 方法,逐步将整个数组调整为大根堆。
siftDown 方法:向下调整逻辑(以大堆为例子)
public void siftDown(int parent, int usedSize){int child = 2 * parent + 1;//确保child(子节点下标)在数组的有效范围内while (child < usedSize) {//elem[child + 1]这里可能会产生child + 1 的空
// if(elem[child] < elem[child + 1]){
// child++;
// }//判断右子节点是否存在且更大,如果是child不就往后移动if(elem[child] < elem[child + 1] && child + 1 < usedSize){//先判断右子节点是否存在(child+1 < size);
//若存在,比较左右子节点的值,把较小的子节点下标用child标记child++;}//代码走到这里 表示 迟来的下标一定是醉倒的孩子下标}}
}
- child = 2 * parent + 1:根据父节点下标,计算左孩子下标(堆的顺序存储特性)。
- 条件判断 if(elem[child] < elem[child + 1] && child + 1 <
usedSize):判断右孩子是否存在且更大,若满足则将 child 指向右孩子 —— 这样 child 就代表了父节点的最大子节点下标。 - 后续会基于 child
下标,比较父节点与最大子节点的大小,若父节点更小则交换二者位置,并继续向下调整(这段代码未完整写出交换逻辑,但结构是向下调整的核心框架)。
把一个普通数组通过 “向下调整” 的方式,逐步构建成大根堆
i - f(elem[child] > elem[parent]):判断当前子节点(已确定是父节点的最大子节点)的值是否大于父节点。如果成立,说明这对父子不满足大根堆的 “父≥子” 规则,需要调整。
- int temp = elem[parent]; elem[parent] = elem[child]; elem[child] =
temp;:交换父节点和子节点的元素,让大的元素上浮到父节点位置。 - parent = child; child = 2*parent+1;:更新父节点为当前子节点的下标,然后计算新的左孩子下标
——继续向下调整下一层子树,确保调整后整个子树都满足大根堆的性质。
public void createHeap() {
//(usedSize - 1 - 1) / 2 是计算堆中最后一个非叶子节点的下标for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {siftDown(parent,usedSize);}}/*** 向下调整的方法* @param parent 每棵子树的根节点下标* @param usedSize 每棵子树是否调整结束的位置*/private void siftDown(int parent, int usedSize) {int child = 2 * parent + 1;//说明 至少有一个左孩子//至少有一个左孩子//elem[child + 1]这里可能会产生child + 1 的空
// if(elem[child] < elem[child + 1]){
// child++;
// }while (child < usedSize) {if(child+1 < usedSize && elem[child] < elem[child+1]) {child++;}//代码走到这里 表示 child下标 一定是最大孩子的下标if(elem[child] > elem[parent]) {//交换swap(child,parent);parent = child;child = 2*parent+1;}else {break;}}}
完全二叉树的特性是:最后一个非叶子节点的子节点,是堆中 “最后一个元素”(叶子节点)。
数组下标的父子关系
在堆的数组存储中,若某个节点的下标为 child(叶子节点),则其父节点的下标为 (child - 1) / 2(整数除法)。
例如:若最后一个元素的下标是 4(即 usedSize - 1 = 4),则它的父节点下标为 (4 - 1) / 2 = 1(整数除法,3/2=1)。
(usedSize - 1 - 1) / 2 是计算堆中最后一个非叶子节点的下标
堆的底层是完全二叉树,存储在数组中,遵循以下下标关系:
- 若某个节点的下标为 i,则其左子节点下标为 2*i + 1,右子节点下标为 2*i + 2。
- 反过来,若某个子节点的下标为 child,则其父节点下标为 (child - 1) / 2(整数除法)。
- usedSize - 1 是堆中最后一个元素的下标(因为 usedSize 是有效元素个数,数组下标从 0 开始)。
- (usedSize - 1 - 1) / 2 等价于 (最后一个元素的下标 - 1) / 2,即通过最后一个元素(叶子节点)的下标,计算出它的父节点下标 —— 这个父节点就是堆中最后一个非叶子节点
堆的时间复杂度:
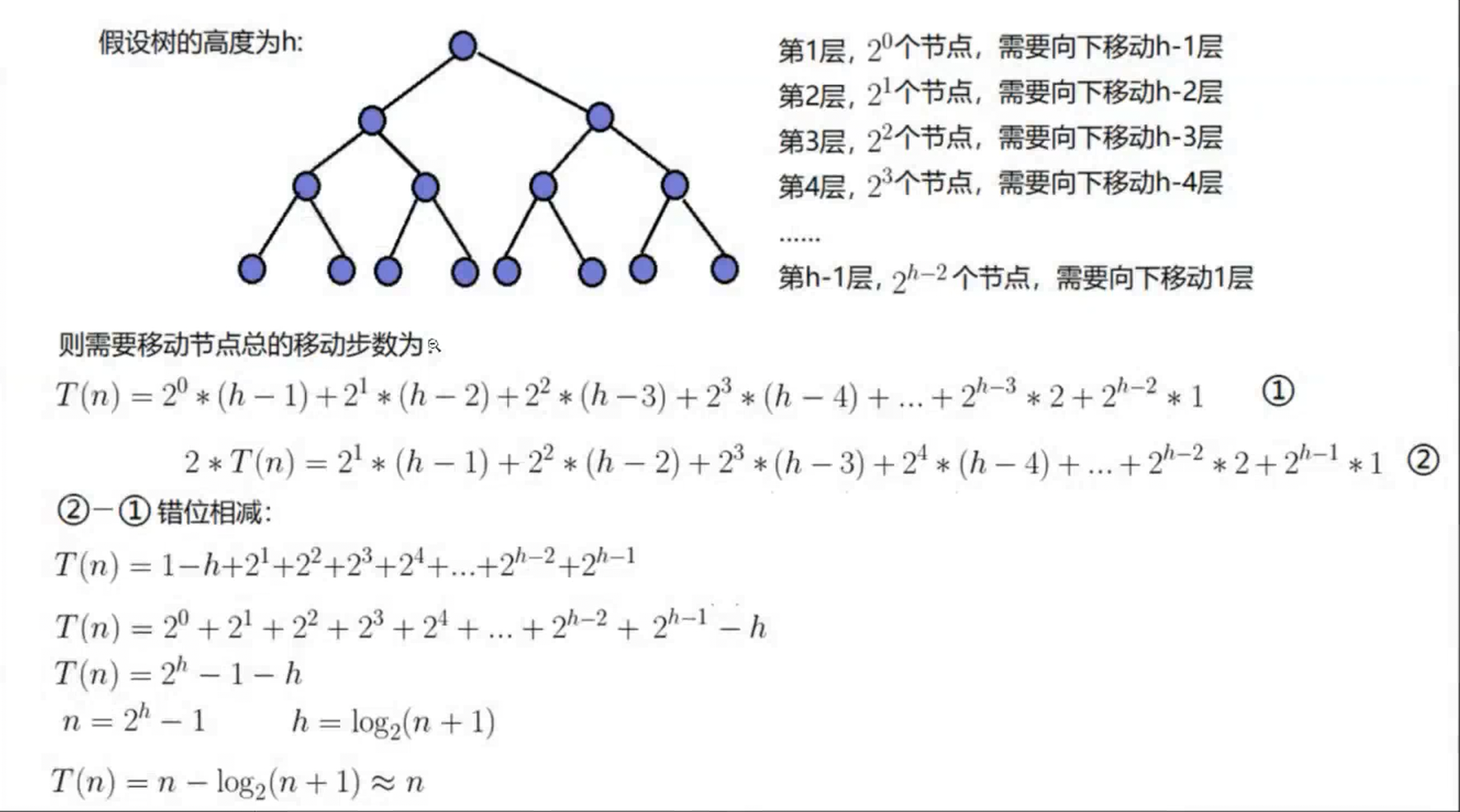
建堆的时间复杂度为O(N)。
