【机器学习02】梯度下降、多维特征线性回归、特征缩放

---

视频链接
吴恩达机器学习p10-p21

---

一、梯度下降算法

在上一篇文章中，我们定义了代价函数 J(w, b)，并明确了我们的目标是找到能使其最小化的参数 w 和 b。但是，我们如何才能系统性地、自动地找到这个最小值点呢？

答案就是梯度下降（Gradient Descent算法。这是一个应用极其广泛的优化算法，不仅用于线性回归，也贯穿于后续更复杂的机器学习模型中。

1.1 核心思想

梯度下降的整体思路非常直观。

概括来说，算法的执行流程如下：

1. 初始化：随机选择一个起始点，即为 w 和 b 赋一个初始值（通常设为0）。
2. 迭代更新：持续地、小步地改变 w 和 b，确保每一步都朝着使代价函数 J(w, b) 减小的方向前进。
3. 收敛：当 J(w, b) 的值不再显著下降，或者说我们到达了一个（局部）最低点时，算法停止。

为了更形象地理解这个过程，吴恩达老师给出了一个非常经典的比喻：

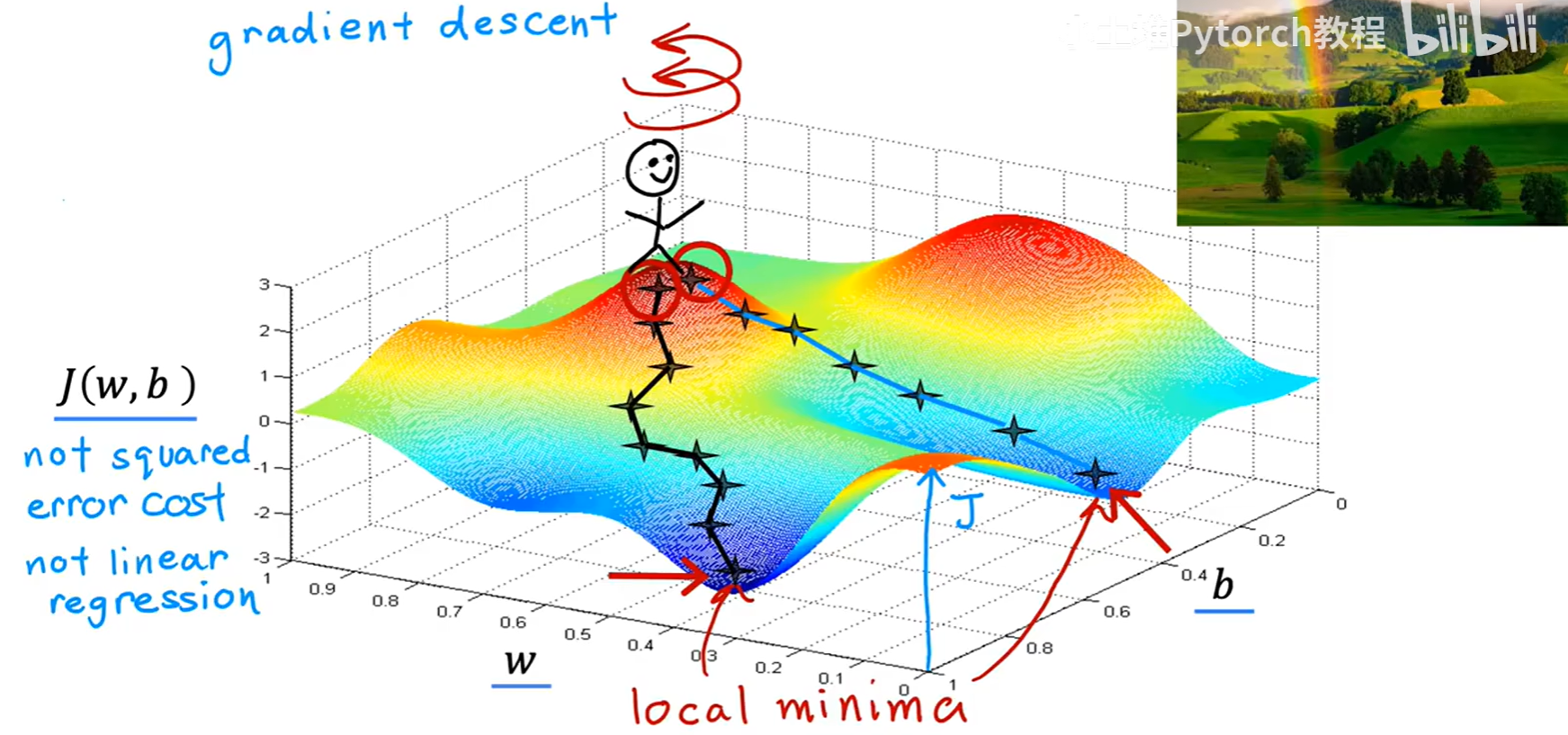
想象一下你正站在一座崎岖不平的山上（这座山就是我们的代价函数曲面），你的目标是尽快走到山谷的最低点。由于雾很大，你无法直接看到最低点在哪里。

一个合理的策略是：环顾四周，找到当前位置最陡峭的下山方向，然后朝着这个方向迈出一步。到达新位置后，再次重复这个过程：环顾四周，找最陡的下山方向，再迈一步。

持续这个过程，你最终就会走到一个山谷的谷底，即一个局部最低点（local minima）。这就是梯度下降算法的核心直觉。

1.2 算法详解

现在，我们用数学语言来精确描述梯度下降算法。

1.2.1 更新规则

梯度下降算法的核心是下面这个不断重复的更新过程，直到算法收敛：

w = w - α * (∂/∂w)J(w,b)
b = b - α * (∂/∂b)J(w,b)

我们来拆解一下这个公式：

• := 或 = ：在编程中，这代表赋值（Assignment操作。即计算出右边的值，然后更新左边的变量。
• α (alpha)：被称为学习率（Learning Rate）。它是一个超参数，控制着我们每一步“下山”的步子迈多大。
• (∂/∂w)J(w,b)：这是代价函数 J 对参数 w 的偏导数（Partial Derivative）。在微积分中，导数代表了函数在某一点的斜率，或者说是变化最快的方向。这个导数项告诉我们，在当前的点，哪个方向是“最陡峭”的。

因此，整个更新规则的含义就是：当前 w 的值，减去学习率 α 乘以代价函数在该点的梯度（斜率）。对 b 的更新也是同理。

1.2.2 重要细节：同步更新

在执行梯度下降时，有一个非常关键的实现细节：必须同步（Simultaneously）更新 w 和 b。

正确的做法是：

1. 在当前 (w, b) 的位置，分别计算出对 w 和 b 的偏导数。
2. 用临时变量 tmp_w 和 tmp_b 存储计算出的新值。
3. 将 tmp_w 赋值给 w，将 tmp_b 赋值给 b。

错误的做法是：

1. 先计算并更新 w。
2. 然后用已经更新过的 w，去计算对 b 的偏导数，并更新 b。

这会导致算法的路径发生偏差，得到错误的结果。

1.3 直观理解梯度下降

为了更深入地理解这个更新公式为什么能奏效，我们再次简化问题，暂时只考虑参数 w，即最小化 J(w)。

1.3.1 导数项的作用：指明方向

导数 d/dw J(w) 实质上就是代价函数曲线在当前 w 点的切线斜率。

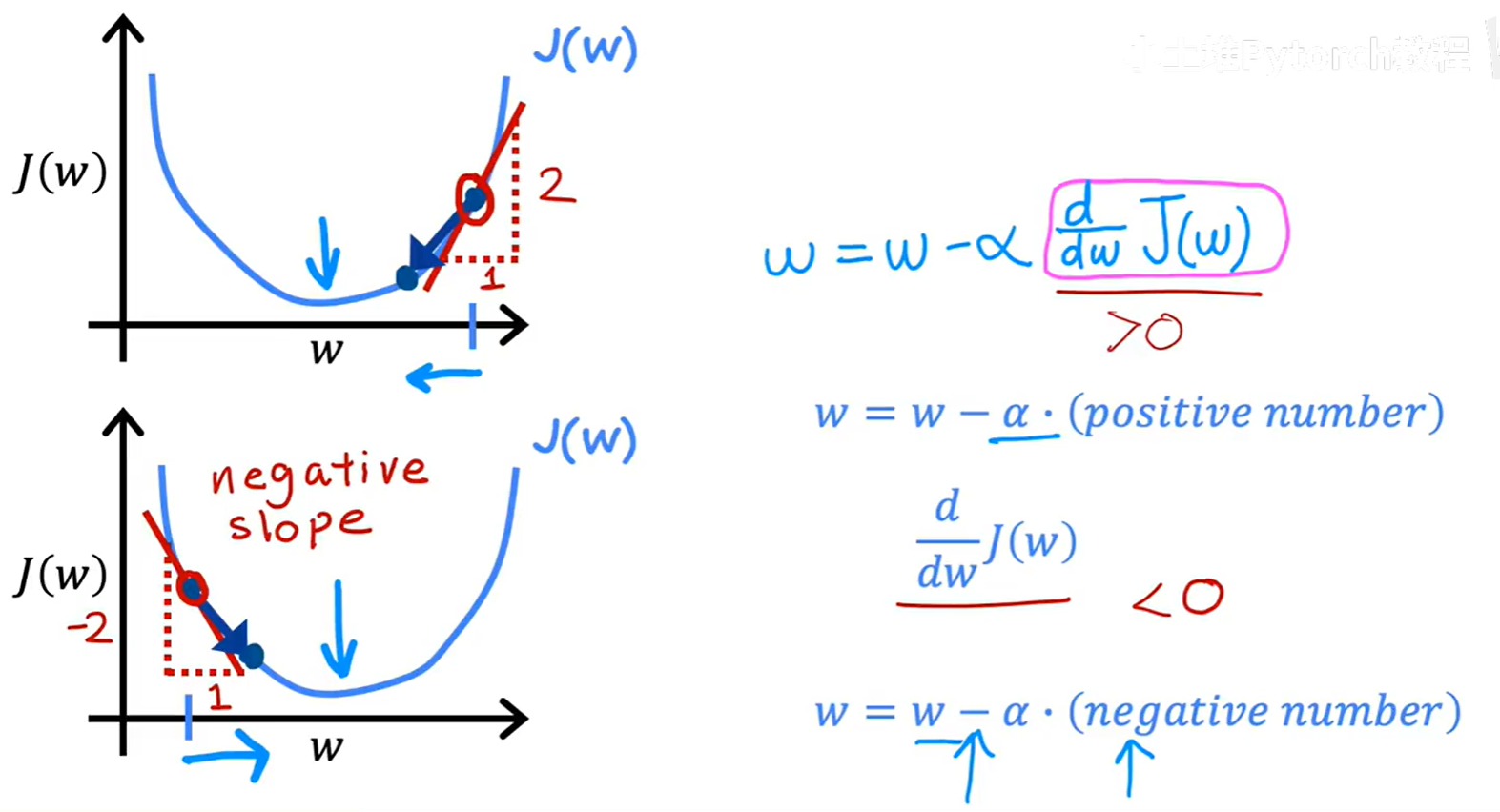
• 情况一：导数 > 0
  当 w 处于最低点的右侧时，曲线的斜率为正。此时，w 的更新量 α * (正数) 为正，w 的新值 w - (正数) 将会变小，即向左移动，靠近最低点。
• 情况二：导数 < 0
  当 w 处于最低点的左侧时，曲线的斜率为负。此时，w 的更新量 α * (负数) 为负，w 的新值 w - (负数) 将会变大，即向右移动，同样靠近最低点。

所以，无论我们从哪边开始，导数项都像一个“指南针”，永远指向能让代价函数下降的方向。

1.3.2 学习率 α 的作用：决定步长

学习率 α 控制着每一步更新的幅度。α 的选择至关重要。

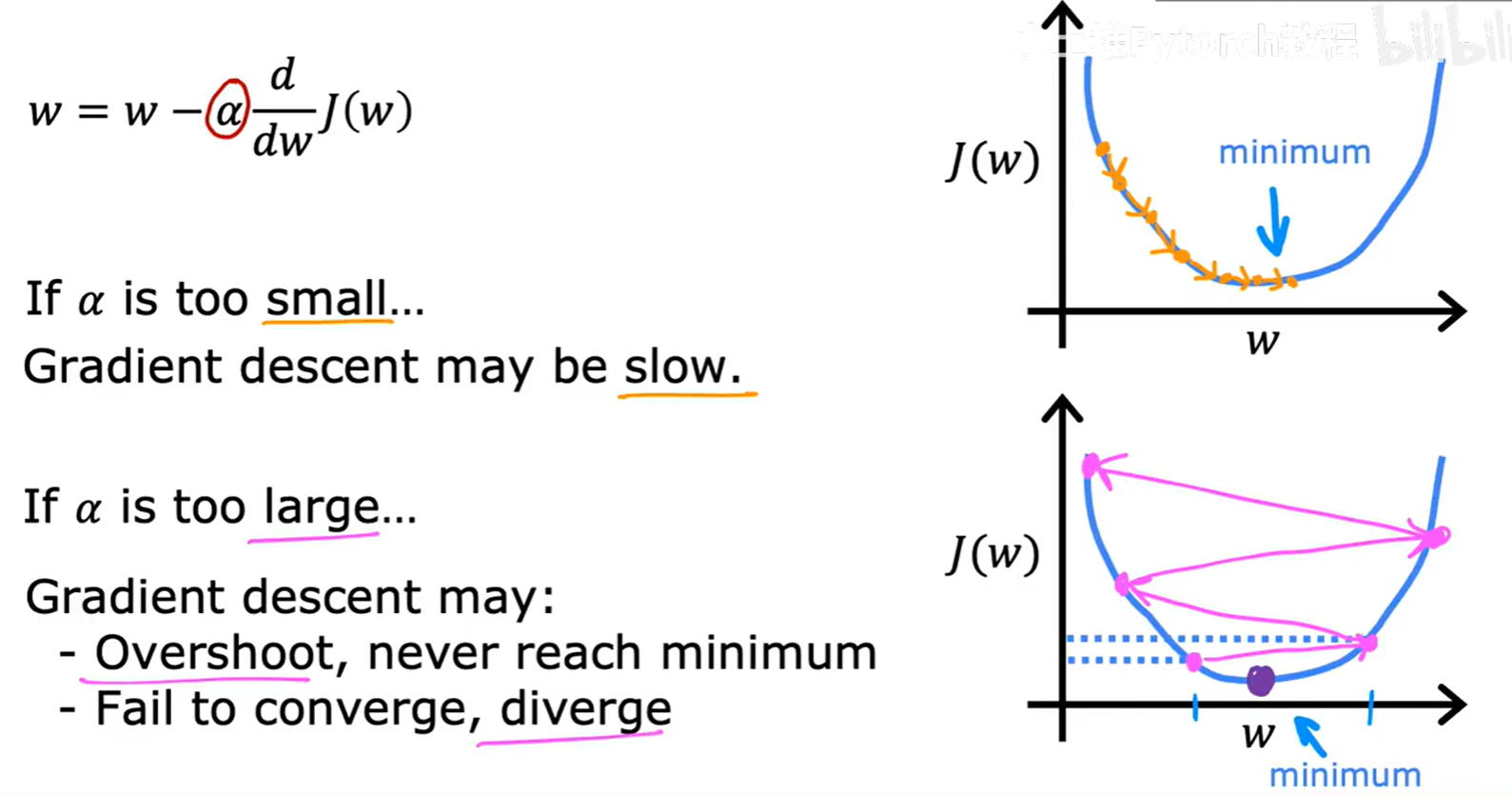
• 如果 α 太小：
  每次更新的步长会非常小，导致算法需要很多很多步才能到达最低点，收敛速度会很慢。
• 如果 α 太大：
  每次更新的步长过大，可能会直接“跨过”最低点，导致在最小值附近来回震荡，无法收敛，甚至可能越过对面更高的山坡，导致代价值越来越大而发散。

因此，选择一个合适的学习率是使用梯度下降算法的关键一步。

1.4 梯度下降的特性

• 在局部最小值点会停止更新
  
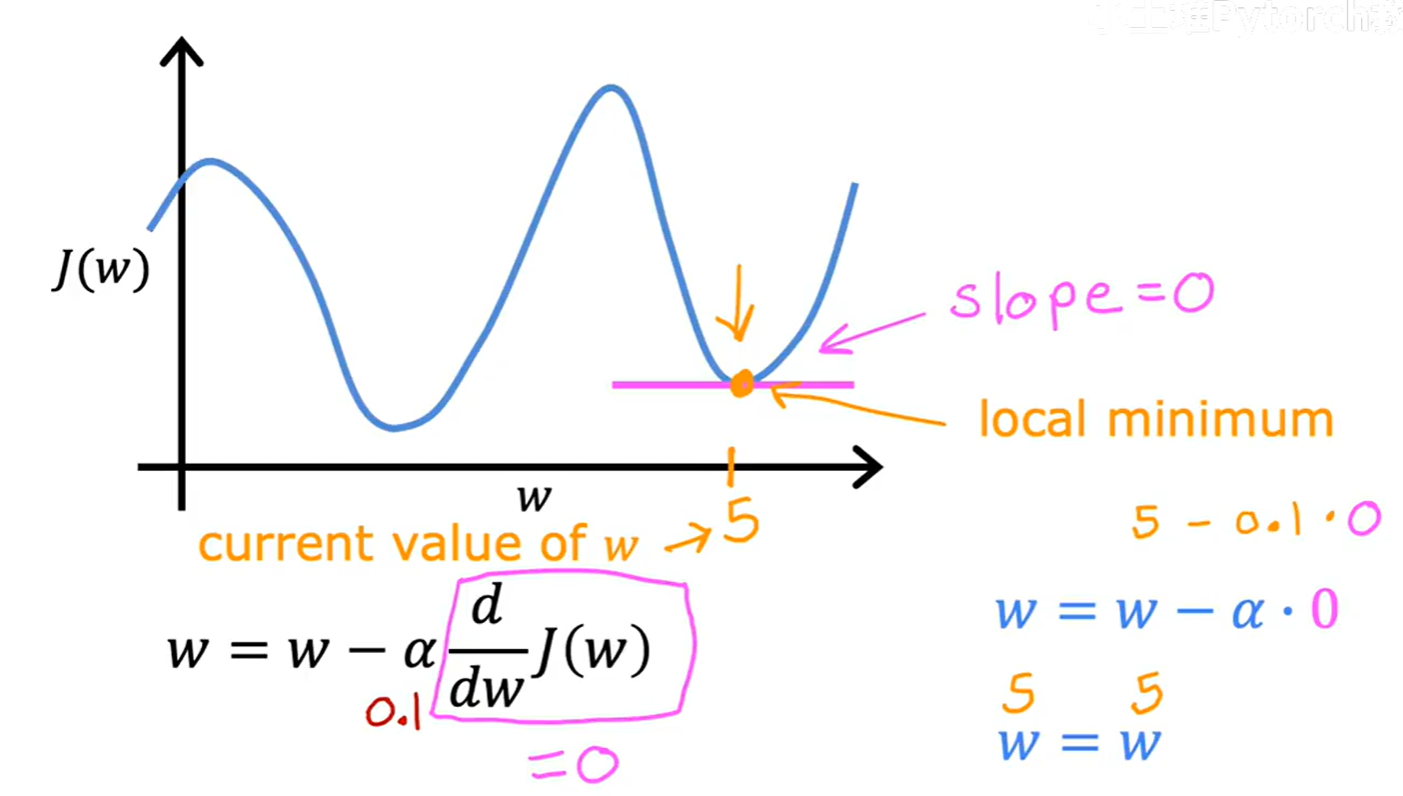
  当 w 到达一个局部最低点时，该点的切线斜率（导数）为0。此时，更新量 α * 0 = 0，w 的值将不再改变，算法自然收敛。

• 即使学习率 α 固定，更新步长也会自动变小
  
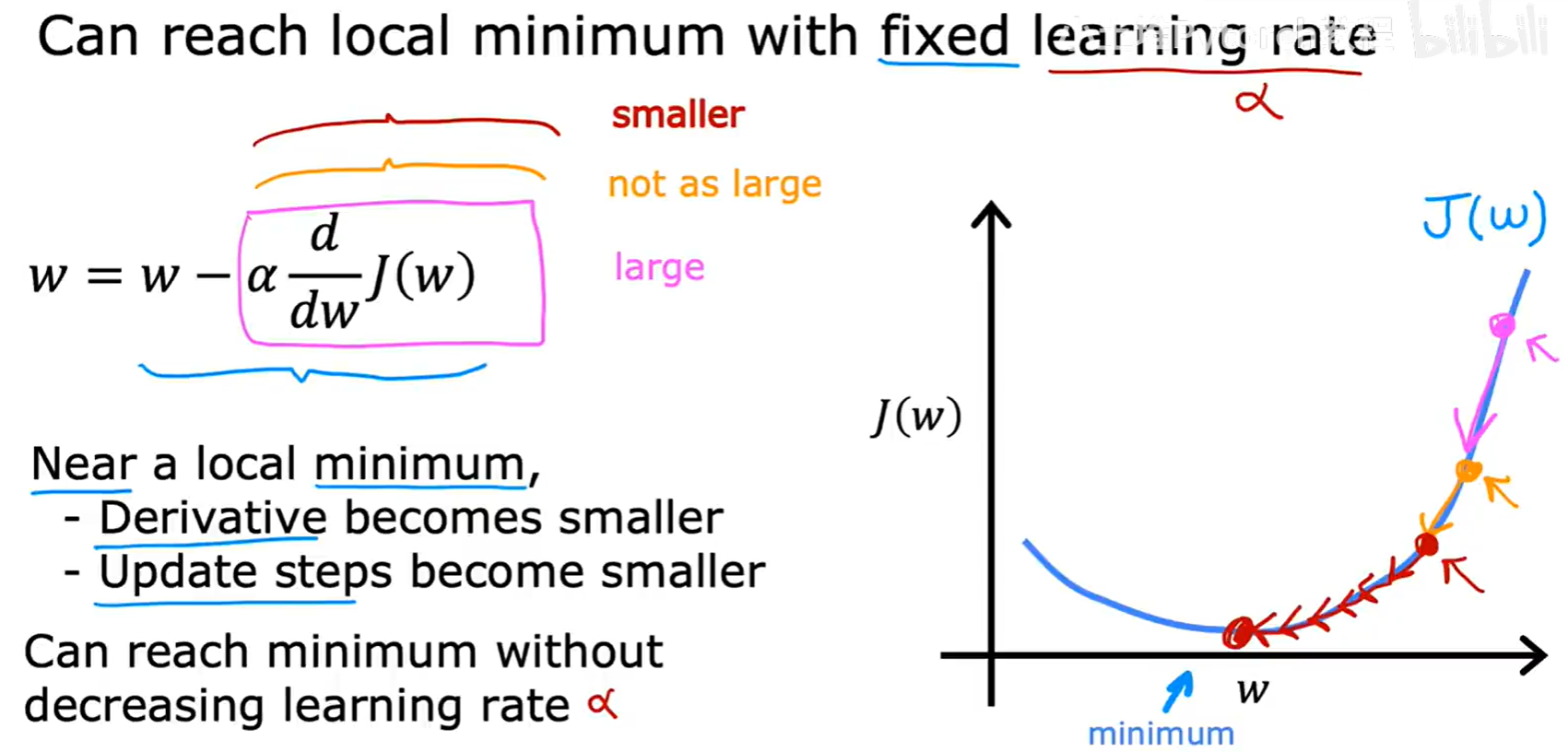
  这是一个非常好的特性。当我们接近最低点时，曲线会变得越来越平缓，导数的值也自然会越来越小。这就意味着，即使 α 是一个固定的值，α * (导数) 这个整体的更新步长也会自动减小。这使得梯度下降可以在接近最优解时进行更精细的调整，从而平稳地收敛到最低点，而不需要我们手动去减小 α。

1.5 梯度下降用于线性回归

现在，我们将这个通用的梯度下降算法，应用到我们之前为线性回归定义的平方误差代价函数上。

1.5.1 线性回归的梯度

我们需要计算出平方误差代价函数 J(w, b) 对 w 和 b 的偏导数。吴恩达老师在课程中给出了推导结果（这部分微积分计算是选学内容）：

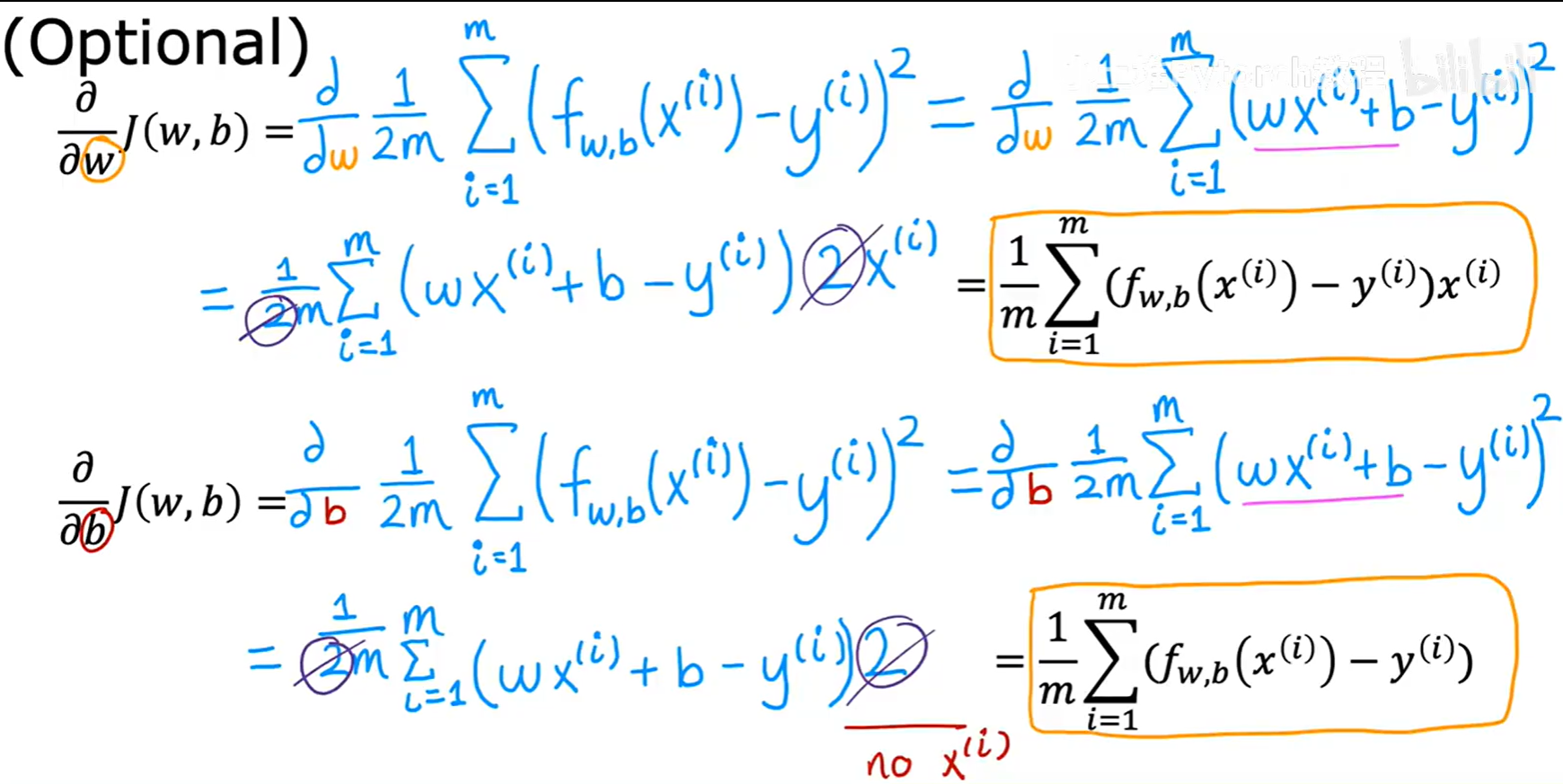
∂/∂w J(w,b) = (1/m) * Σ [ (f(x⁽ⁱ⁾) - y⁽ⁱ⁾) * x⁽ⁱ⁾ ] (从 i=1 到 m)
∂/∂b J(w,b) = (1/m) * Σ [ (f(x⁽ⁱ⁾) - y⁽ⁱ⁾) ] (从 i=1 到 m)

其中，f(x⁽ⁱ⁾) = wx⁽ⁱ⁾ + b。将这两个具体的导数公式，代入到通用的梯度下降更新规则中，我们就得到了线性回归的完整学习算法。

1.5.2 凸函数与全局最优解

我们之前提到，梯度下降可能会陷入局部最低点。

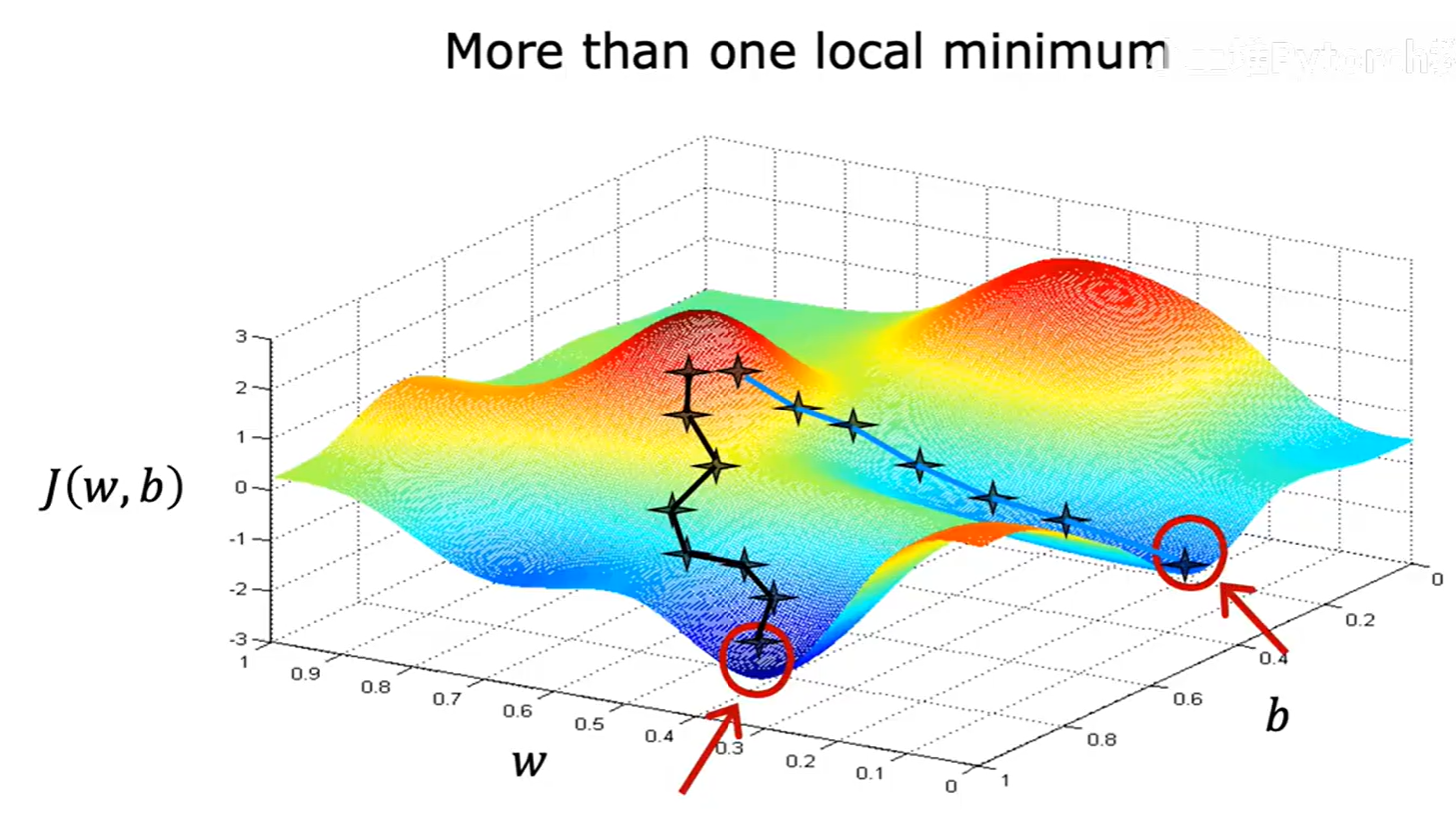
幸运的是，用于线性回归的平方误差代价函数是一个凸函数（Convex function）。从图形上看，它是一个完美的“碗”形，没有任何局部的凹陷。

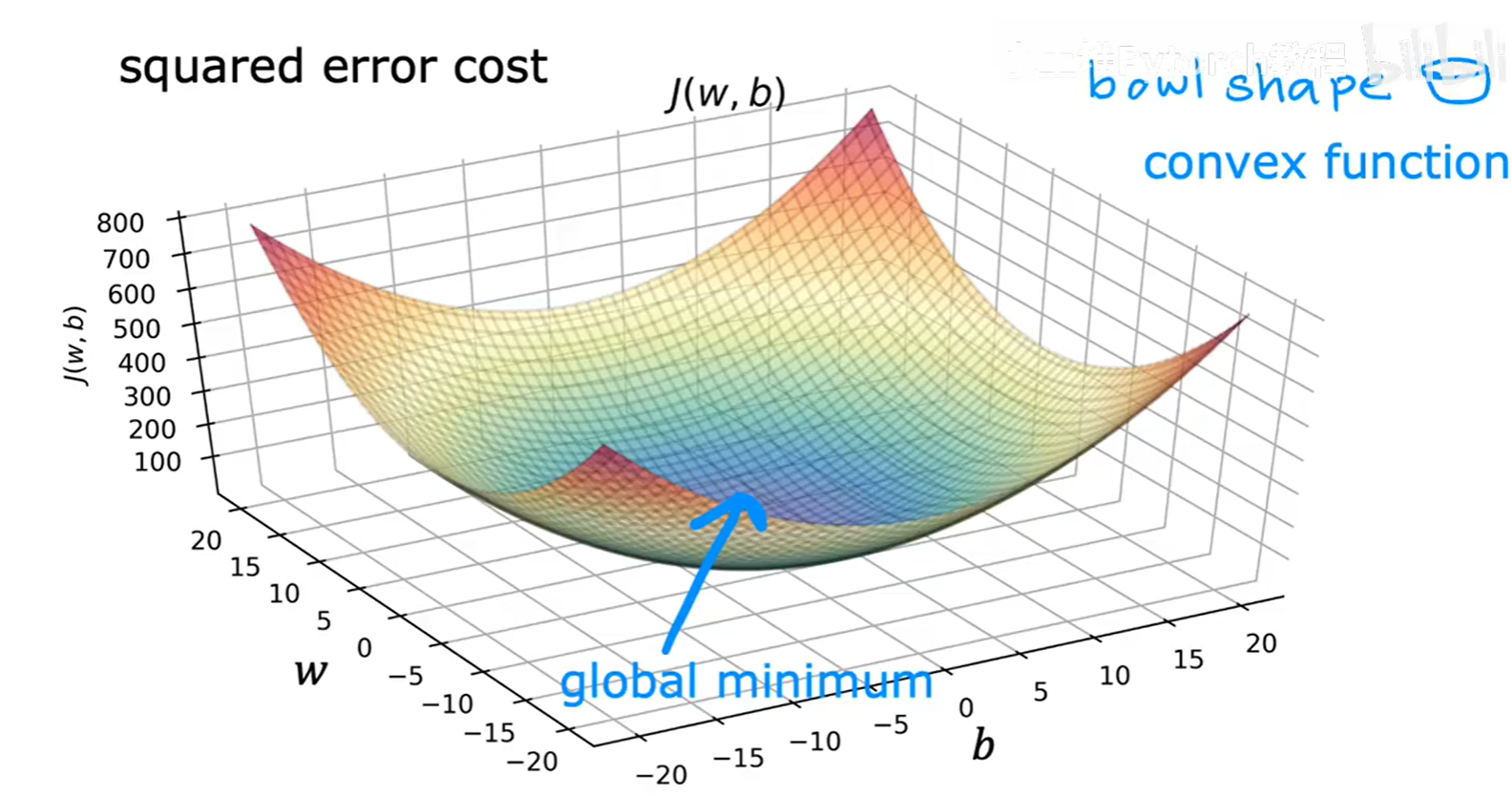
这意味着它只有一个最低点，这个点既是局部最低点，也是全局最低点（global minimum）。

因此，只要我们正确地使用梯度下降算法，就一定能为线性回归找到全局最优的参数 w 和 b。

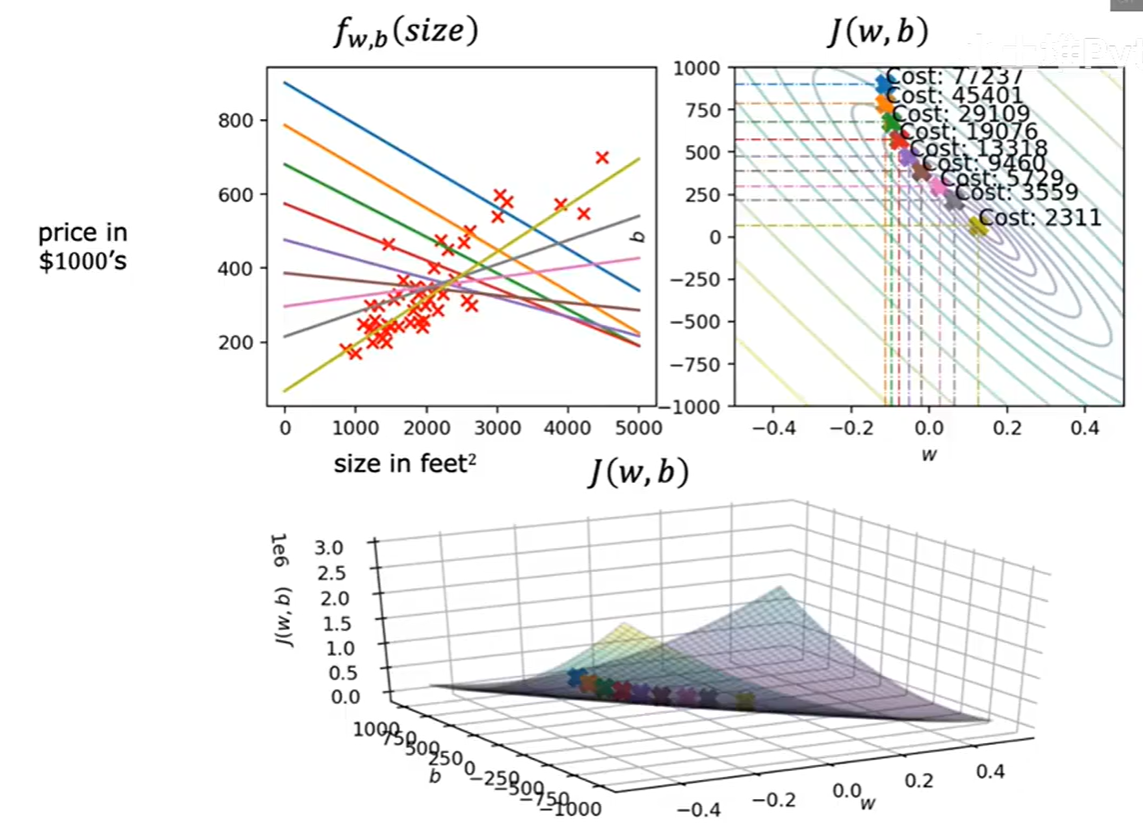
上图生动地展示了梯度下降在线性回归代价函数上的工作过程。随着迭代的进行，参数 (w, b) 在右侧的等高线图上一步步走向中心最低点，同时，左侧的模型拟合直线也在数据点中逐步调整到最优的位置。

1.6 “批”梯度下降 (Batch Gradient Descent)

我们目前学习的这种梯度下降算法，有一个特定的名字，叫做批 梯度下降（“Batch” Gradient Descent）。

这里的“批（Batch）”指的是，在计算梯度并更新参数的每一步中，我们都使用了全部（整个一批的训练样本（从 i=1 到 m）。

在后续的课程中，我们还会接触到其他类型的梯度下降算法，它们在每一步中可能只使用训练集的一个子集。但目前，我们所说的梯度下降，默认指的就是“批”梯度下降。

二、多维特征的线性回归

到目前为止，我们只用了一个特征（房屋面积）来预测房价。但在现实中，决定房价的因素远不止一个，比如卧室数量、楼层数、房龄等等。当我们的模型包含多个特征时，就进入了多维特征的线性回归（Multiple Linear Regression），也常被称为多元线性回归。

2.1 新的符号表示

为了处理多个特征，我们需要对之前的符号进行扩展。

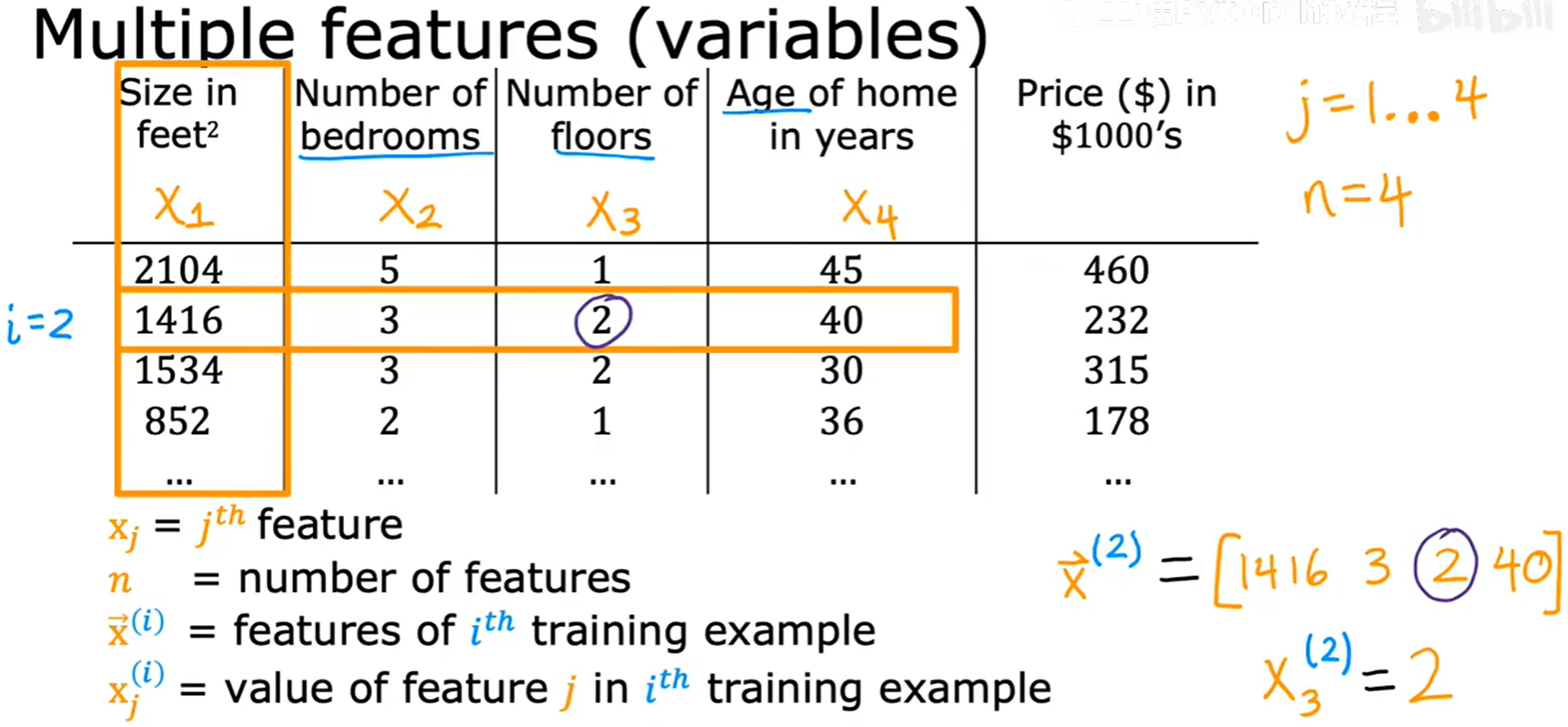
• n: 表示特征的总数。在上图中，我们有4个特征，所以 n=4。
• xⱼ: 表示第 j 个特征。例如，x₁ 是房屋面积，x₂ 是卧室数量。
• x⃗⁽ⁱ⁾: 表示第 i 个训练样本的所有特征，它是一个向量（vector）。例如，x⃗⁽²⁾ = [1416, 3, 2, 40]。
• xⱼ⁽ⁱ⁾: 表示第 i 个训练样本中，第 j 个特征的值。例如，x₃⁽²⁾ = 2，代表第二个样本的楼层数是2。

2.2 多维特征的模型表示

单个特征时，我们的模型是 f(x) = wx + b。当有多个特征时，模型会为每个特征分配一个对应的参数（权重），形式如下：

f(x) = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

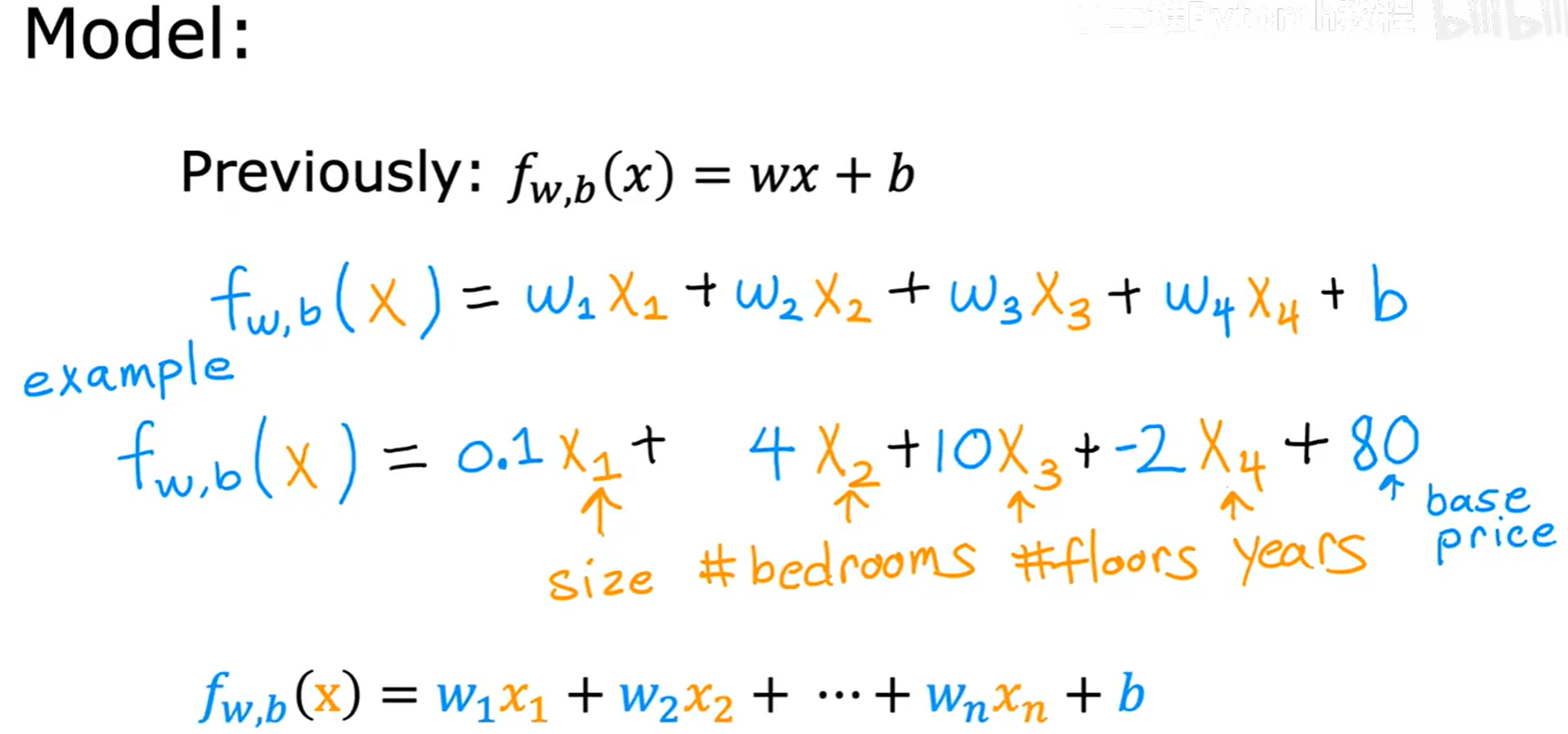
例如，一个包含4个特征的房价预测模型可能是：f(x) = 0.1x₁ + 4x₂ + 10x₃ - 2x₄ + 80。这里的 w₁=0.1 就代表了面积对房价的影响，而 b=80 可以理解为一个基础房价。

2.2.1 向量化表示

为了让这个公式更简洁、计算更高效，我们引入向量化（Vectorization的表示方法。

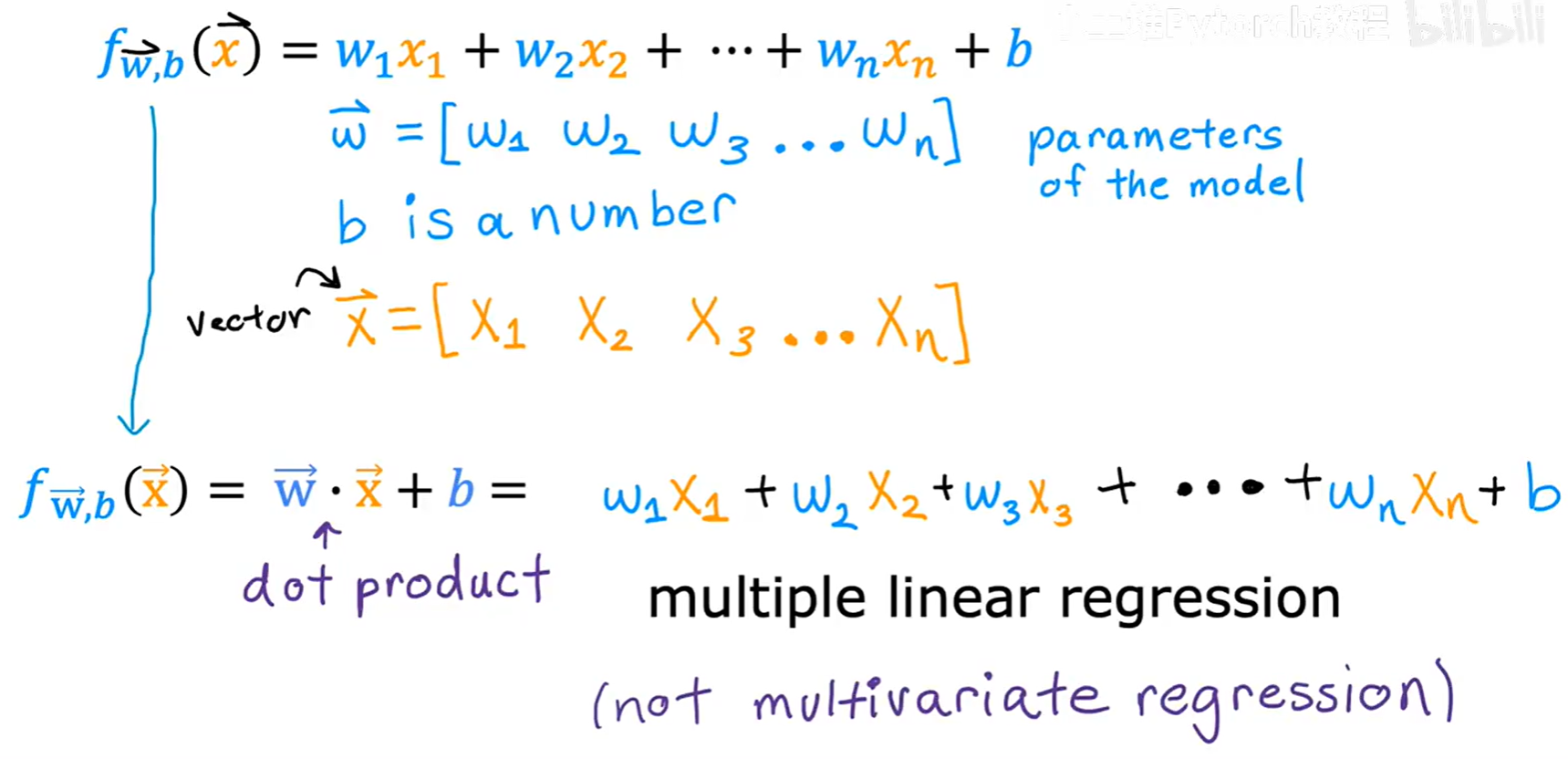
• 我们将所有的参数 w 组合成一个向量：w⃗ = [w₁, w₂, ..., wₙ]
• 我们将所有的输入特征 x 组合成一个向量：x⃗ = [x₁, x₂, ..., xₙ]
• 参数 b 依然是一个单独的数值。

这样，模型就可以用向量的**点积（dot product）**来表示：

f_w⃗,b(x⃗) = w⃗ · x⃗ + b

这种表示方法不仅在数学上更优雅，在代码实现中也更为高效。

2.3 向量化的威力

向量化是利用现代计算库（如 Python 中的 NumPy）和硬件（CPU/GPU）并行计算能力的关键。它能用更少的代码实现更快的运算。

以上图为例，要计算 w⃗ · x⃗，如果不使用向量化，我们需要写一个 for 循环，逐个计算 w[j] * x[j] 并累加。而使用向量化，我们只需要一行代码 np.dot(w, x)。

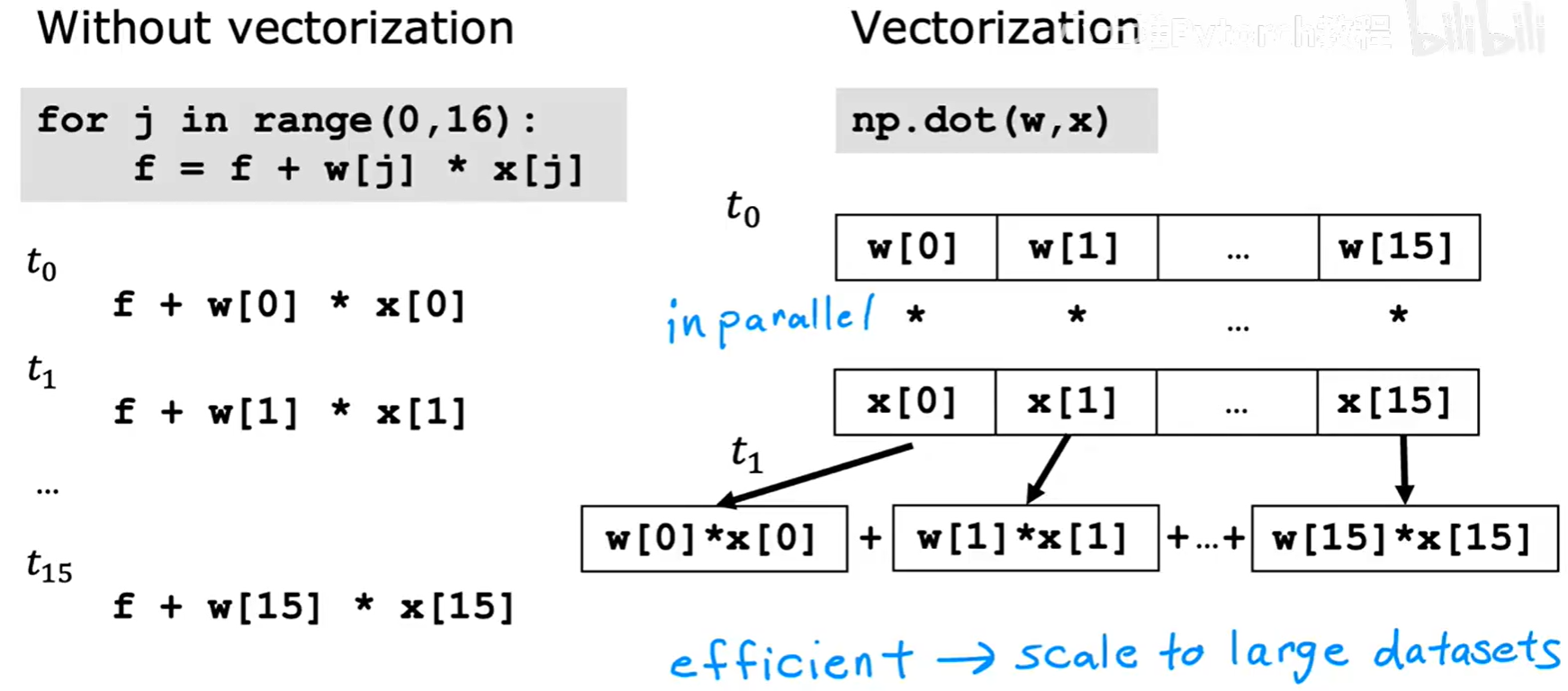
这背后的原理是，for 循环是串行计算，一步一步执行。而向量化的点积操作，可以利用底层硬件实现并行计算，一次性完成所有元素的乘法和加法，当特征数量 n 很大时（例如成千上万），向量化的计算速度会比 for 循环快得多。

在梯度下降的更新过程中，向量化同样能发挥巨大作用：

原本需要用 for 循环逐个更新的 wⱼ，现在可以通过向量运算一次性完成对整个 w⃗ 向量的更新。

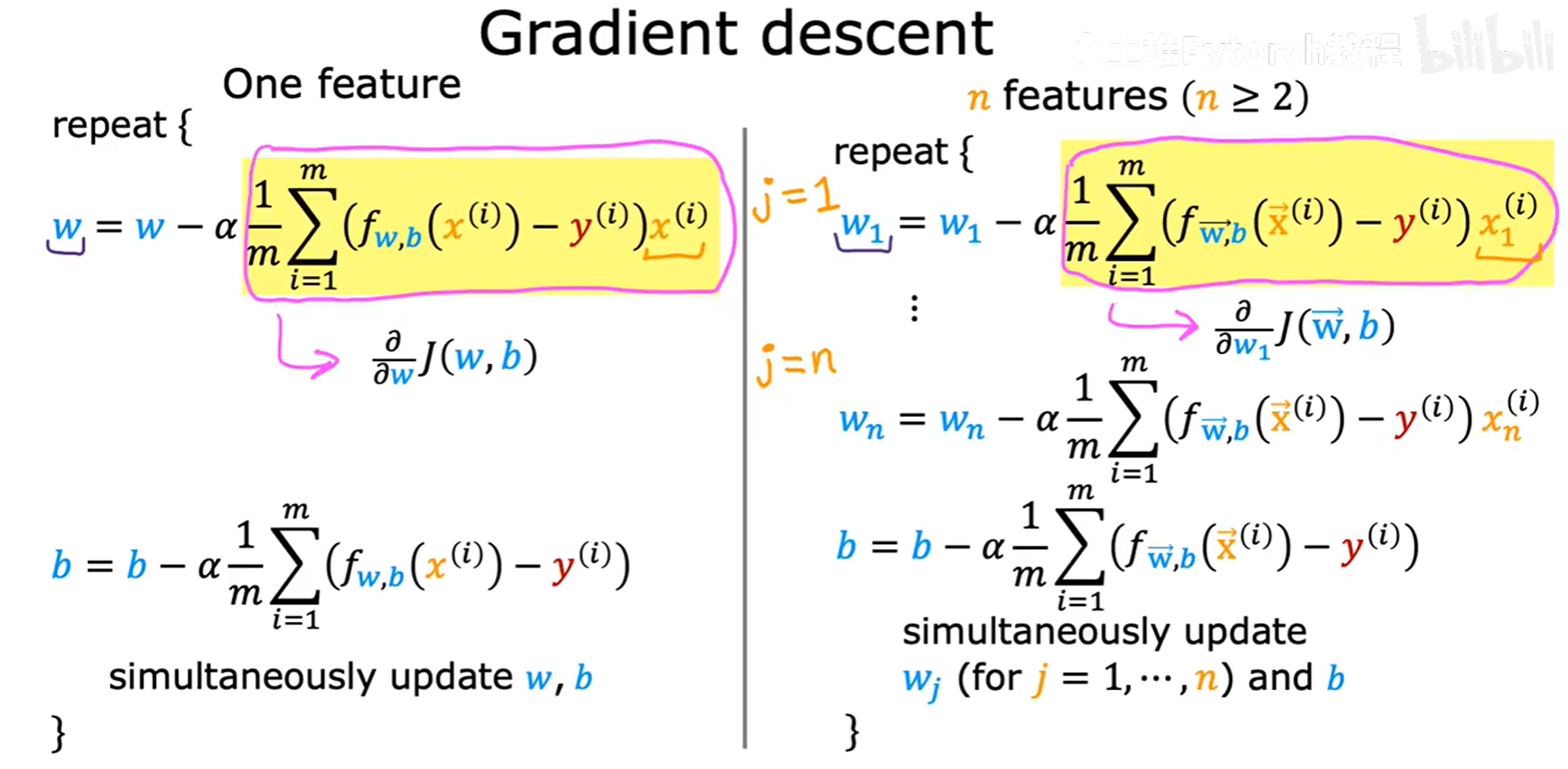
2.4 多维特征的梯度下降

引入多维特征后，我们的核心算法——梯度下降，其框架保持不变，只是需要为每一个参数 wⱼ（从 j=1 到 n）和参数 b 计算偏导数并进行更新。

总结一下符号的演变：

• 参数: 从 w, b 变为向量 w⃗ 和标量 b。
• 模型: 从 f(x) = wx + b 变为 f(x⃗) = w⃗ · x⃗ + b。
• 代价函数: 从 J(w, b) 变为 J(w⃗, b)。
• 梯度下降: 从更新 w 和 b 变为同步更新 w₁...wₙ 和 b。

2.5 正规方程 (Normal Equation) - 选学

除了梯度下降，还有一种被称为正规方程（Normal Equation的方法可以用来求解线性回归的参数。

• 优点: 它是一个纯数学解法，不需要像梯度下降那样进行多次迭代，也无需选择学习率 α。
• 缺点:
  1. 它只适用于线性回归，无法推广到更复杂的模型。
  2. 当特征数量 n 非常大时（例如超过10,000），其计算复杂度会急剧增加，运行速度会非常慢。

因此，梯度下降是更通用、更主流的优化算法。

三、特征缩放 (Feature Scaling)

特征缩放是应用机器学习，特别是梯度下降时，一个至关重要的数据预处理步骤。它能显著提升梯度下降的收敛速度和稳定性。

3.1 为什么需要特征缩放？

让我们来看一个例子，有两个特征：房屋面积 x₁（取值范围 300-2000）和卧室数量 x₂（取值范围 0-5）。这两个特征的取值范围相差巨大。

这会导致一个问题：与范围较小的特征（如 x₂）相比，范围较大的特征（如 x₁）最终可能会对应一个数值非常小的参数 w₁，而 x₂ 则会对应一个数值较大的参数 w₂。

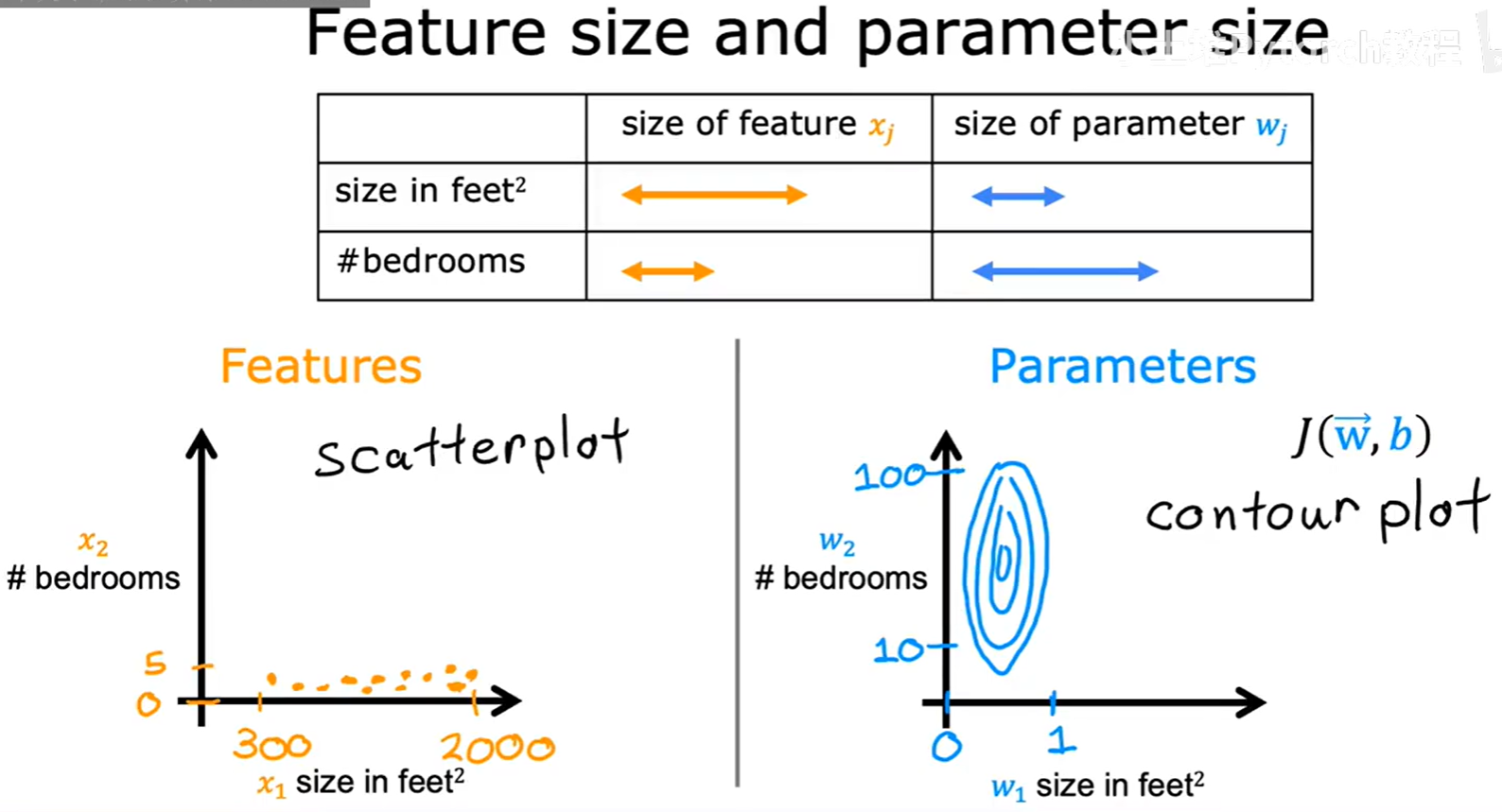
当不同参数 w 的取值范围差异巨大时，代价函数的等高线图会被“压扁”和“拉长”，形成一个非常瘦高的椭圆形。

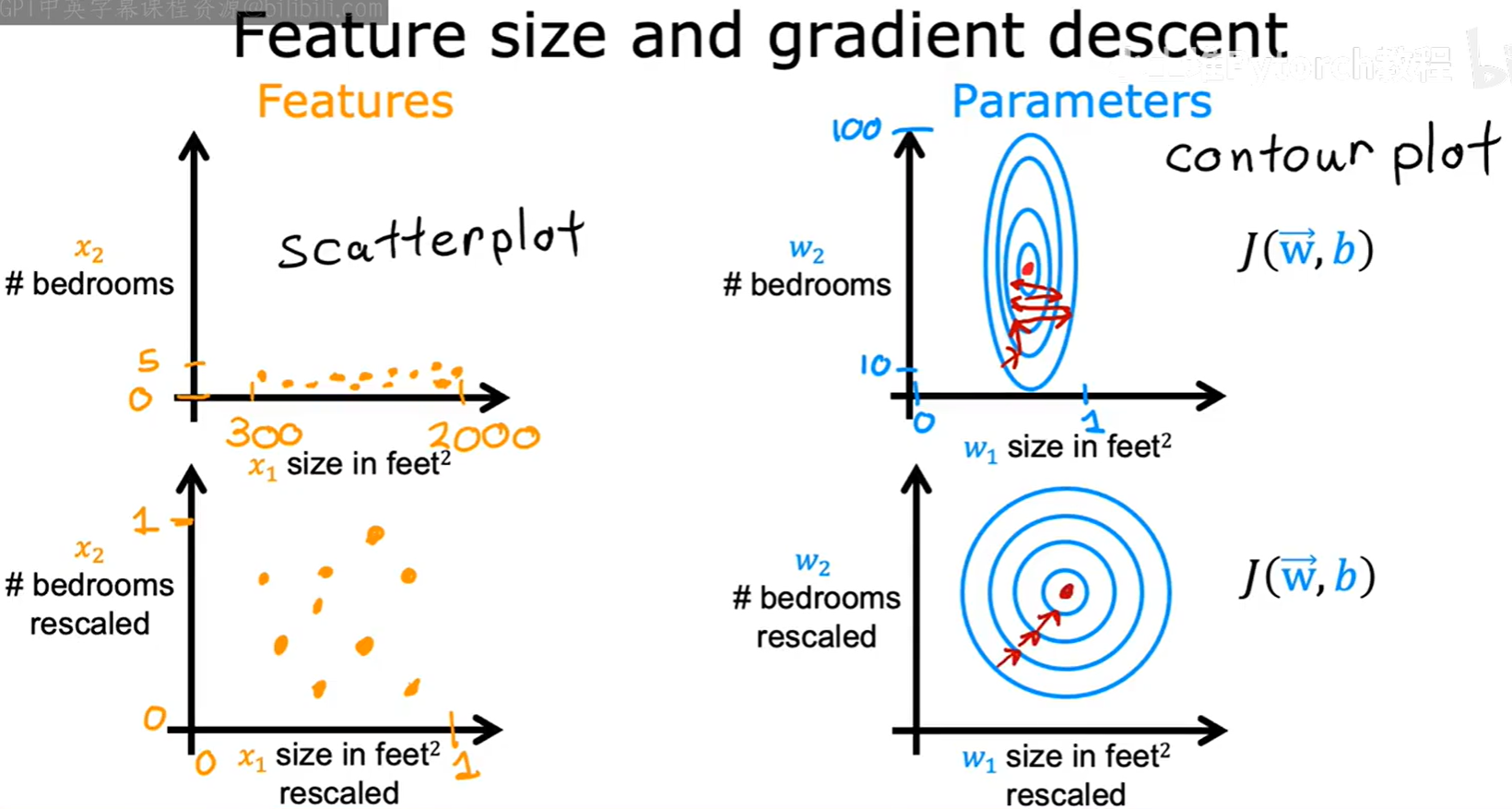
在这种“地形”上进行梯度下降，算法会像在一个狭长的山谷中一样，来回震荡，需要走很多“冤枉路”才能到达最低点，收敛速度会非常慢。

3.2 特征缩放的目标

如果我们通过某种方法，将所有特征的取值范围都缩放到一个相似的区间（例如 0 到 1），那么代价函数的等高线图就会变得更“圆”。

在更“圆”的代价函数曲面上，梯度下降算法可以沿着更直接的路径，更快地找到全局最小值。

3.3 特征缩放的方法

常用的特征缩放方法有以下几种：

3.3.1 最大值归一化 (Max Scaling)

这是最简单的方法之一，将每个特征的值除以该特征的最大值。

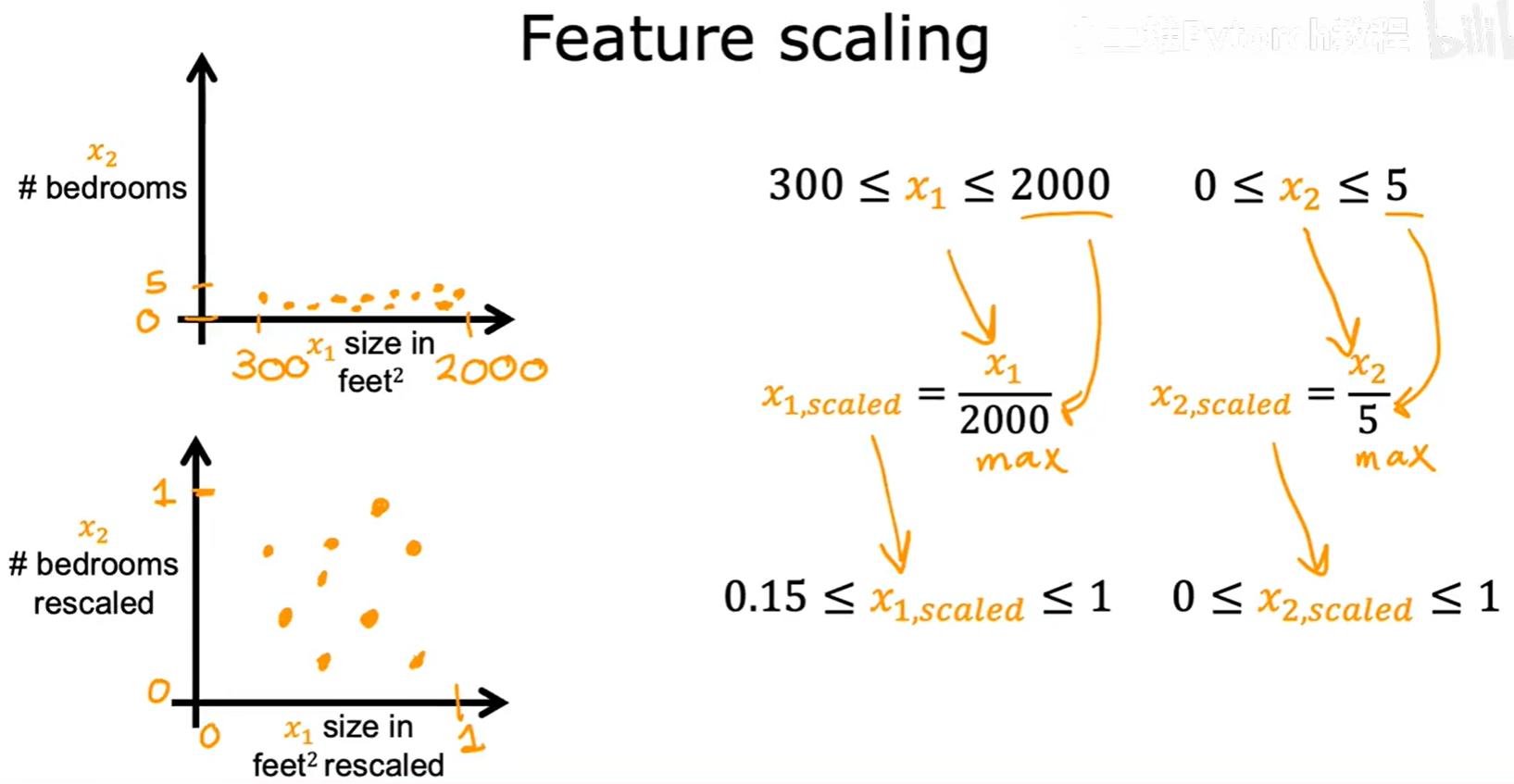
x₁,scaled = x₁ / 2000
x₂,scaled = x₂ / 5

这样可以将特征缩放到 [0, 1] 或 [0.15, 1] 这样的区间内。

3.3.2 均值归一化 (Mean Normalization)

该方法将特征值减去其平均值，再除以其取值范围（最大值 - 最小值）。

x₁ = (x₁ - μ₁) / (max - min)
x₂ = (x₂ - μ₂) / (max - min)

这样处理后，特征的均值会变为0，取值范围大致在 -0.5 到 0.5 之间。

3.3.3 Z-score 标准化 (Z-score Normalization)

这是非常常用的一种标准化方法。它将特征值减去其平均值，再除以其标准差 σ。

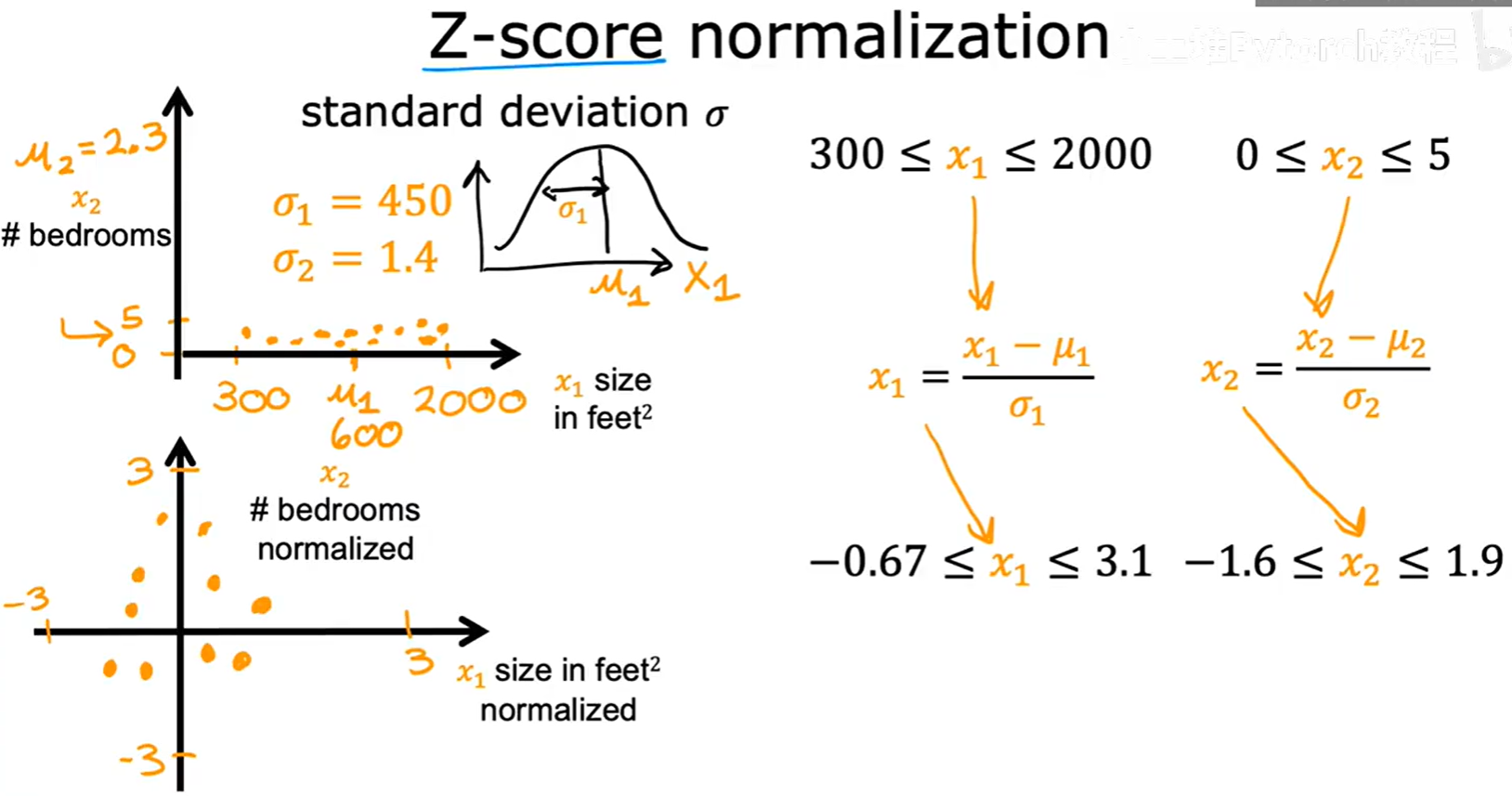
x₁ = (x₁ - μ₁) / σ₁
x₂ = (x₂ - μ₂) / σ₂

处理后的数据将服从均值为0，标准差为1的标准正态分布。

3.4 特征缩放的经验法则

在实践中，我们并不需要严格地将所有特征都缩放到完全相同的范围。一个通用的经验法则是：尽量将每个特征 xⱼ 的范围控制在 -1 到 1 附近。

• 像 -1 到 1，0 到 1，-2 到 0.5 这样的范围都是可以接受的。
• 像 -3 到 3 或 -0.3 到 0.3 的范围也问题不大。
• 但如果一个特征的范围是 -100 到 100，或者 -0.001 到 0.001，那么就应该考虑进行特征缩放了。

正确地使用特征缩放，是让你的机器学习模型高效、稳定运行的关键一步。