【机器视觉-基础知识】三角测量（Triangulation）

三角测量（Triangulation）原理解析

一、基本定义

三角测量（Triangulation） 是通过两台（或多台）相机的投影信息，计算空间点三维坐标的一种方法。

已知：

• 两个相机的投影矩阵 $P_1,P_2$
• 同一空间点在两幅图像中的对应点 $p_1,p_2$

目标是：
求出三维点 $X=[X,Y,Z,1{]}^{\mathsf{T}}$ 的坐标。

---

二、几何直观

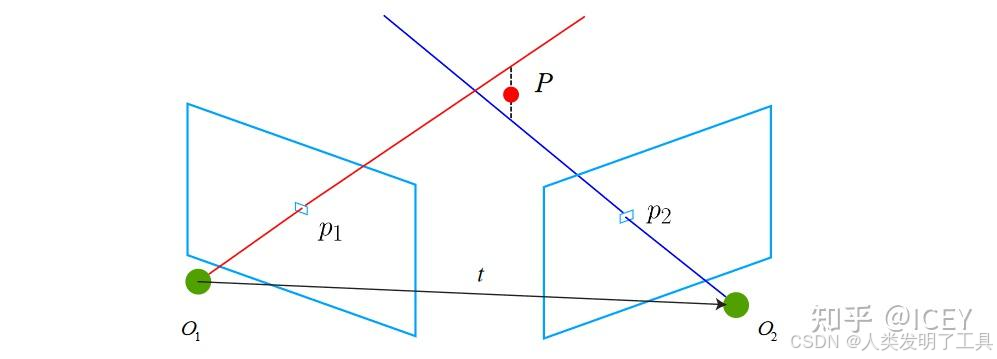
从几何上看：

• 空间点 $X$ 经过两个相机投影到图像上，形成 $p_1$ 和 $p_2$
• 由相机中心 $O_1$、$O_2$ 及点 $X$ 构成一个三角形
• 因此称为 “三角测量（Triangulation）”

三角测量的本质：
通过两条视线（射线）的交点来恢复空间点的三维位置。

---

三、基本数学模型

1. 齐次坐标投影方程

空间点 $X$ 与图像点 $p$ 的关系为：

$$p\sim PX$$

其中：

• $P=K[R|t]$ 为相机投影矩阵
• $p=[x,y,1{]}^{\mathsf{T}}$ 为图像点的齐次坐标
• “$\sim$” 表示相差一个比例因子$s$（同线性）

$$sp=PX$$
比例因子 $s$ 实际上就是该三维点在相机坐标系下的深度 $Z_c$。

对于两台相机：

$$\{\begin{array}{l}{p}_1\sim P_{1}X\\ p_2\sim P_{2}X\end{array}$$

---

四、线性三角化（Linear Triangulation）

对于每个相机的齐次形式投影方程：

$$s_i\left[\begin{array}{c}{u}_i\\ v_i\\ 1\end{array}\right]=P_i\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$

其中，$s_i$ 是尺度因子（深度）。

则对于每一个相机 $i$ 的投影方程：
每个方程有 3 个分量：

$$s_i{u}_i=p_{i1}^{\mathsf{T}}\mathbf{X},s_i{v}_i=p_{i2}^{\mathsf{T}}\mathbf{X},s_i=p_{i3}^{\mathsf{T}}\mathbf{X}$$

其中，$p_{i1},,p_{i2},,p_{i3}$ 分别是 $P_i$ 的第 1、2、3 行向量。

通过消去 $s_i$：

$$u_i,(p_{i3}^{\mathsf{T}}\mathbf{X})=p_{i1}^{\mathsf{T}}\mathbf{X}$$

$$v_i,(p_{i3}^{\mathsf{T}}\mathbf{X})=p_{i2}^{\mathsf{T}}\mathbf{X}$$

将两式改写为线性方程形式：

$$(u_i,p_{i3}^{\mathsf{T}}-p_{i1}^{\mathsf{T}})\mathbf{X}=0$$

$$(v_i,p_{i3}^{\mathsf{T}}-p_{i2}^{\mathsf{T}})\mathbf{X}=0$$

组合两个相机的两视图的方程，可得总共 4 个线性方程：

$$A\mathbf{X}=0$$

其中：

$$A=\left[\begin{array}{c}{u}_1{p}_{13}^{\mathsf{T}}-p_{11}^{\mathsf{T}}\\ v_1{p}_{13}^{\mathsf{T}}-p_{12}^{\mathsf{T}}\\ u_2{p}_{23}^{\mathsf{T}}-p_{21}^{\mathsf{T}}\\ v_2{p}_{23}^{\mathsf{T}}-p_{22}^{\mathsf{T}}\end{array}\right]\text{(矩阵尺寸 }4\times 4)$$

解法：通过最小二乘求解 $AX=0$，即：

$$X=\arg \underset{|X|=1}{\min }|AX|$$

该问题可通过 奇异值分解（SVD） 得到：

$$A=U\Sigma V^{\mathsf{T}}\Rightarrow X=V_{(:,4)}$$

即 $V$ 的最后一列，对应最小奇异值。

通过线性三角化（Linear Triangulation），我们最终求得三维空间点的齐次坐标 $X=[X_1,X_2,X_3,X_4{]}^{\mathsf{T}}$

最后将齐次坐标归一化成：

$$X_{\text{cart}}=\frac{1}{X_4}[X_1,X_2,X_3{]}^{\mathsf{T}}=[X,Y,Z]$$
非齐次坐标 $[X,Y,Z,1{]}^{\mathsf{T}}$

---

五、几何解释：射线交点

从物理几何意义上，三角测量等价于两条射线的交点：

$$\{\begin{array}{l}{r}_1=O_1+{\lambda }_1{\mathbf{d}}_1\\ r_2=O_2+{\lambda }_2{\mathbf{d}}_2\end{array}$$

其中：

• $O_i$ 为相机中心
• ${\mathbf{d}}_i$ 为方向向量（由像素反投影得到）

理论上，两射线应在空间交于一点。
实际由于噪声存在，它们一般不会精确相交，因此取 最近点中点 作为估计点：

$$X=\frac{r_1({\lambda }_1^{\ast })+r_2({\lambda }_2^{\ast })}{2}$$

• r₁(λ₁*)：在射线 r₁ 上的某个点。
• r₂(λ₂*)：在射线 r₂ 上的某个点。这两个点之间的欧氏距离 ||r₁(λ₁*) - r₂(λ₂*)|| 是所有可能点对中最小的。
• 参数 λ₁* 和 λ₂* 就是使这个距离最小化的最优参数。

---

六、改进方法：最优三角化（Optimal Triangulation）

线性方法简单但对噪声敏感。
可通过最小化 重投影误差（Reprojection Error）获得最优结果：

$$\underset{X}{\min }\sum _{i=1}^2|p_i-\pi (P_{i}X){|}^2$$

其中 $\pi (\cdot )$ 表示从齐次坐标到像素坐标的投影操作。

该问题为非线性优化，可通过 高斯–牛顿法（Gauss–Newton） 或 Levenberg–Marquardt 优化求解。

---

七、数值稳定性与注意事项

1. 归一化（Normalization）：
   在进行线性三角化前应对图像点坐标进行归一化，以减少数值误差。

2. 视差角（Baseline）：
   当两相机的基线很短或视差很小，三角测量精度会显著下降。

3. 非线性优化后精化：
   通常先用线性三角化求初值，再以最小重投影误差方式进行迭代精化。

---

八、在 SfM / MVS 中的作用

应用场景	作用
SfM（Structure from Motion）	根据估计的相机姿态恢复三维点云
MVS（Multi-View Stereo）	利用多视图一致性进行密集三维重建
双目匹配（Stereo Matching）	根据左右相机匹配点计算深度（$Z$）

---

九、核心公式回顾

名称	公式	含义
投影方程	$p\sim PX$	空间点到图像点的投影关系
线性方程	$AX=0$	由两幅图像观测建立的约束
SVD 解法	$X=V_{(:,4)}$	最小二乘意义下的三维点解
最优估计	$\min_X \sum_i	p_i - \pi(P_i X)

---

十、总结一句话

三角测量 = 由多视图投影恢复三维点坐标的过程。

它是从二维观测到三维几何的关键步骤，
与极线约束互为几何对应：

极线约束描述“两个点应在同一平面上”，
三角测量计算“该平面与两条视线的交点”。