当前位置：首页 > news >正文

MeshGPT：三角形网格生成的Decoder-Only Transformer范式解析

news 2025/10/16 7:36:17

项目主页：MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers
论文地址：nihalsid.github.io/mesh-gpt/static/MeshGPT.pdf

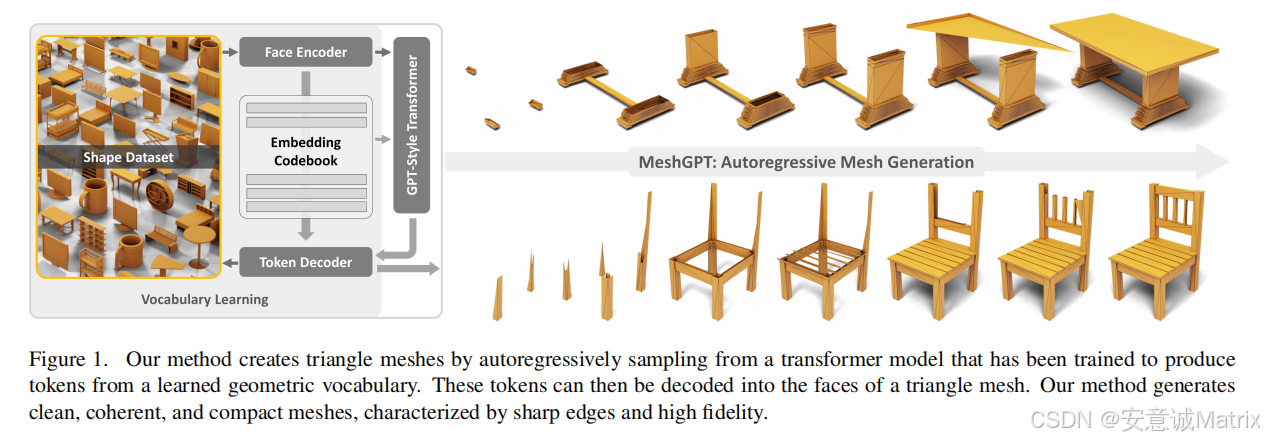
在这里插入图片描述

从机器学习与3D计算机视觉交叉领域的研究视角出发，MeshGPT的核心贡献在于打破了传统3D生成依赖“中间表示后处理”的范式，首次将NLP领域成熟的Decoder-Only Transformer架构与几何感知的表示学习结合，实现了三角形网格的直接、紧凑、高保真自回归生成。本文将从问题建模、技术架构、创新突破、实验验证及领域价值五个维度，系统解析其方法论与科学意义。

一、问题背景与动机：3D网格生成的核心挑战

三角形网格作为3D图形学的“原生表示”，具备拓扑结构化、渲染兼容性强、存储效率高的优势，但其生成任务长期面临两大核心挑战，这也是MeshGPT的研究出发点：

1. 现有3D生成范式的固有缺陷

传统3D生成方法多依赖非网格中间表示，需通过后处理（如Marching Cubes、QEM简化）转换为网格，导致不可避免的质量损失：

体素（Voxel）：受限于网格分辨率，存在“块状伪影”，高分辨率下内存开销爆炸；
点云（Point Cloud）：缺乏拓扑连接性，转换为网格时需解决点云重建的歧义性（如Poisson重建易产生冗余面）；
神经场（Neural Field，如SDF）：虽支持任意拓扑，但iso-surfacing提取的网格存在过细分（Over-tessellation） 问题（如GET3D生成的椅子含27k+面），且边缘平滑、细节丢失（如桌角变圆）。

2. 直接网格生成的技术瓶颈

现有直接网格生成方法（如PolyGen、AtlasNet）未能有效平衡“拓扑连贯性”与“生成效率”：

PolyGen：采用“顶点生成→面生成”双自回归网络，但顶点与面的训练分离导致误差累积（顶点生成未考虑后续面的拓扑需求，面生成依赖固定顶点分布）；
AtlasNet/BSPNet：通过2D平面变形或二叉空间分割生成网格，但前者易产生“折叠伪影”，后者生成的网格拓扑过于规则（块状结构），缺乏真实3D资产的不规则 triangulation 模式。

MeshGPT的核心动机即解决上述问题：设计一种端到端的自回归生成框架，直接输出符合人工建模规律（紧凑、 sharp edges、拓扑合理）的三角形网格。

二、模型架构：几何表示学习与自回归生成的协同设计

MeshGPT的技术框架分为两大核心模块：几何词汇表学习（Geometric Vocabulary Learning） 与 Decoder-Only Transformer生成，二者形成“表示-建模”闭环，具体架构如图1所示。

1. 几何词汇表学习：从三角形到量化嵌入的表示映射

传统自回归生成若直接使用三角形的9维坐标（3个顶点×3维坐标）作为token，会导致序列长度爆炸（N个面需9N个token） 与 几何信息缺失（未捕捉邻接面拓扑）。MeshGPT通过“图卷积编码+残差量化”构建具有拓扑-几何感知的词汇表，解决这一问题。

（1）图卷积编码器：捕捉局部拓扑-几何特征

为建模三角形网格的邻接关联性，MeshGPT将网格抽象为“面图（Face Graph）”：

节点定义：每个节点对应一个三角形，输入特征包括：
- 几何特征：9维顶点坐标（经 positional encoding 增强）、面面积、三边夹角、法向量；
- 拓扑特征：通过邻接矩阵隐式编码（相邻面共享边/顶点）；
编码器结构：采用堆叠的SAGEConv（GraphSAGE的卷积层），通过“聚合邻接节点特征”实现局部几何-拓扑信息融合，输出每个面的576维特征向量 $z_i$ $\in R^{576}$ （N个面对应特征矩阵 $\Z$ $\in R^{N \times 576}$ ）。

关键设计意义：不同于独立处理单个三角形，图卷积编码器使嵌入向量蕴含“面与面的依赖关系”（如椅子腿的面与座面的面特征存在关联），为后续生成连贯拓扑奠定基础。

（2）残差向量量化（Residual Vector Quantization, RQ）：压缩与离散化

为降低序列长度并实现“词汇表化”，MeshGPT采用深度为D=6的残差量化（而非传统VQ-VAE的单级量化）：

量化策略：将每个面的576维特征 $z_i$ 按顶点拆分（3个顶点×192维/顶点），对每个顶点特征进行 $\ D/3=2$ 级量化，最终每个面对应6个量化token $t_i = [t_i^1, ..., t_i^6]$ ；
代码本更新：采用指数移动平均（EMA）动态更新代码本 $\mathcal{C}$ （大小16384），平衡量化精度与更新稳定性；
序列长度优化：传统坐标token序列长度为9N，RQ后为6N（D=6），当N=300时序列长度从2700降至1800，适配Transformer的上下文窗口（论文用4608）。

创新点：顶点级量化（Per-Vertex Quantization）而非面级量化，使共享顶点的面具有相似token，进一步强化拓扑连贯性（如桌腿与桌面共享的顶点量化token一致，确保生成时面的连接性）。

（3）ResNet解码器：重建约束与词汇表有效性验证

为确保量化token可准确解码为三角形，MeshGPT设计1D ResNet-34解码器：

输入：量化token序列 $T = [t_1, ..., t_N]$ （每个token映射为代码本嵌入 $e(t_i^d)$ ）；
输出：离散化的9维顶点坐标（空间离散为128³网格，输出坐标的类别分布而非连续值）；
损失函数：
- 重建损失：交叉熵损失（离散坐标预测），通过“平滑one-hot权重”降低物理邻近坐标的惩罚；
- 承诺损失（Commitment Loss）：约束量化嵌入与原始特征的距离，避免量化误差过大。

2. Decoder-Only Transformer：自回归网格生成

基于预训练的几何词汇表，MeshGPT采用GPT-2-medium架构（24层自注意力、16头、768维隐藏层）实现自回归生成，核心设计如下：

（1）序列建模策略

序列排序：沿用PolyGen的“顶点索引排序”规则——顶点按z-y-x轴升序排序，面按最小顶点索引排序，确保生成时拓扑的一致性；
位置编码：采用双级位置编码：
- 面级编码：标识当前token所属面在序列中的位置；
- 嵌入级编码：标识当前token在面内6个嵌入中的索引（如 $t_i^1$ 与 $t_i^2$ 的编码不同），解决面内嵌入的顺序歧义；
输入序列构造：每个训练样本的序列为 $\ [\text{<start>}, t_1^1, t_1^2, ..., t_1^6, t_2^1, ..., t_N^6, \text{<end>}]$ ，模型目标是最大化条件概率 $\prod_{i=1}^N \prod_{d=1}^6 p(t_i^d | t_{<i}, t_i^{<d})$ 。