[tile-lang] 语言接口 | `T.prim_func` `@tilelang.jit` | 底层原理

第1章：TileLang语言接口（T命名空间）

欢迎来到TileLang

在本章中，我们将介绍如何使用熟悉的Python语法编写超高速GPU和CPU代码的核心方式：T命名空间。

为什么选择T命名空间？高性能计算的Python化遥控器

想象你要烘焙一个复杂的蛋糕。你可以亲自精确称量每种原料、手工搅拌并完美计时每个步骤。这就像用CUDA或HIP等语言编写底层GPU代码——功能强大但极其繁琐，需要大量专业知识

现在想象你有一个智能厨房助手。只需告诉它"烘焙巧克力软糖蛋糕"，它就能高效处理所有称量、搅拌和烘焙工作。这正是TileLang想要为高性能计算实现的目标。

T命名空间（通过import tilelang.language as T访问）就是你在TileLang中的"遥控器"或"智能助手"。这是一个特殊的Python工具集，让你能用Python风格描述想要计算什么，而无需陷入硬件细节的泥潭。TileLang会将高级描述自动转换为针对GPU/CPU的极致高效代码。

本章目标：学完本章后，将掌握如何使用T命名空间编写基础的矩阵乘法(GEMM)内核——这是许多AI模型的基础构建模块。

T命名空间工具箱

让我们拆解T命名空间中最重要的工具，这些工具将用于构建高性能内核。

1. 内核蓝图：T.prim_func与@tilelang.jit

当编写需要TileLang转换为超快GPU/CPU内核的Python函数时，需要明确告知：“注意，这不是普通Python函数，这是我的内核蓝图”

这通过两个关键部分实现：

• @tilelang.jit：这是一个"装饰器"(特殊的Python标记)，告诉TileLang进行即时(JIT)编译生成机器代码。就像按下"编译"按钮
• @T.prim_func：这个装饰器将函数标记为"原始函数"——GPU/CPU计算的主入口点

import tilelang
import tilelang.language as T# 这个装饰器告诉TileLang编译此函数
@tilelang.jit
def my_first_kernel(M, N):# 这个装饰器将内部函数标记为实际内核逻辑@T.prim_funcdef kernel_logic(A: T.Tensor((M, N), "float32"),  # 输入张量AB: T.Tensor((M, N), "float32"),  # 输入张量BC: T.Tensor((M, N), "float32"),  # 输出张量C):# ... 内核计算代码放在这里 ...pass # 稍后填充！return kernel_logic# 使用方式：
# compiled_kernel = my_first_kernel(1024, 1024)

说明：外层my_first_kernel函数定义了在内核运行前固定的参数如M和N

内部kernel_logic函数是实际GPU/CPU计算的所在。注意A、B和C都使用T.Tensor声明——这告诉TileLang它们的形状和数据类型。

2. 数据描述：T.Tensor

在计算前，需要告知TileLang数据的形状(如2D矩阵或1D列表)和数据类型(如半精度float16或单精度float32)

T.Tensor正是为此设计

# 在你的@T.prim_func内部：
# A: T.Tensor((M, K), dtype)
# 声明输入A是一个2D矩阵(M行K列)
# 数据类型为"float16"或"float32"等

说明：T.Tensor((M, K), dtype)指定了一个多维数组

(M, K)描述其形状，dtype指定数据类型。这与PyTorch等库中定义张量的方式类似。

3. 工作线程设置：T.Kernel

GPU上，许多"工作线程"并行运行代码。这些线程被组织成称为"线程块"的组。T.Kernel用于定义需要多少块以及每块包含多少线程。

# 在你的@T.prim_func内部：
# with T.Kernel(num_blocks_x, num_blocks_y, threads=num_threads_per_block) as (bx, by):
#     # ... 这个'with'块内的代码在GPU上运行 ...

说明：

• T.ceildiv(N, block_N)：这个实用函数计算ceil(N / block_N)。用于确定覆盖整个N维度需要多少块，假设每块处理block_N个元素。
• threads=128：表示每个工作组(线程块)有128个独立工作线程。
• (bx, by)：这些特殊变量告知每个块在块网格中的唯一坐标。bx是块的X坐标，by是Y坐标。

4. 工作内存：T.alloc_shared与T.alloc_fragment

GPU有不同类型的内存，有些更快但更小(像厨师的砧板)，有些更慢但更大(像大储藏室)。

• T.alloc_shared：分配"共享内存"。这是非常快速的小内存，同一块内所有线程都可使用。就像团队的共享白板。
• T.alloc_fragment：分配"片段内存"。这更快，本质上是每个线程专用的寄存器。就像每个工作者的私人记事本。

# 在T.Kernel上下文中：
A_shared = T.alloc_shared((block_M, block_K), dtype) # A的共享内存块
B_shared = T.alloc_shared((block_K, block_N), dtype) # B的共享内存块
C_local = T.alloc_fragment((block_M, block_N), accum_dtype) # 结果私有寄存器

说明：这里我们分配共享内存来临时保存矩阵A和B的小"块"(tile)以便线程快速访问。C_local是每个线程用于累积部分结果的私有片段。

5. 清理暂存区：T.clear

就像在白板上开始新头脑风暴前要擦干净一样，T.clear在开始累积结果前将T.alloc_fragment内存清零。确保计算从干净状态开始。

# 在T.Kernel上下文中：
T.clear(C_local) # 确保本地累加缓冲区为空

6. 数据搬运：T.copy

为最大化性能，数据需要在全局内存(慢速、大容量)和共享/片段内存(快速、小容量)间移动。T.copy显式搬运这些数据块。

# 在T.Kernel上下文中：
# 将A的一个块从全局内存(A)复制到共享内存(A_shared)
T.copy(A[by * block_M, ko * block_K], A_shared)

说明：这行代码将A矩阵的一个矩形区域(“块”)从全局内存复制到A_shared。by * block_M和ko * block_K计算当前块的起始坐标。

7. 并行循环：T.Parallel

要真正发挥GPU威力，需要并行运行操作。T.Parallel将标准Pythonfor循环转换为并行循环，不同迭代由不同线程处理。

# 在T.Kernel上下文中：
for i, j in T.Parallel(block_M, block_N):# ... 此循环内的操作并行运行 ...

说明：如果block_M是128且block_N是128，此循环逻辑上会运行128 * 128次，可用线程(如T.Kernel中的128线程)协作处理这些迭代的一部分。

8. 核心计算：T.gemm

矩阵乘法(GEMM)是关键操作。T.gemm是TileLang中高度优化的内置函数，对小数据"块"执行矩阵乘法，通常使用专用硬件指令(如NVIDIA GPU上的Tensor Core)。

# 在T.Kernel上下文中：
T.gemm(A_shared, B_shared, C_local) # 将A_shared与B_shared相乘，结果存入C_local

说明：这一行是强大指令

它告诉TileLang对A_shared块和B_shared块执行优化矩阵乘法，结果存入C_local片段。TileLang自动找出针对特定硬件的最佳方式。

构建基础矩阵乘法内核

让我们组合这些概念编写简单矩阵乘法内核。使用README.md示例的简化版，专注于T命名空间元素。

import tilelang
import tilelang.language as T
import torch # 用于后续测试# 1. 用@tilelang.jit定义内核函数
@tilelang.jit
def matmul_kernel_builder(M, N, K, block_M, block_N, block_K, dtype="float16", accum_dtype="float"):# 2. 用@T.prim_func定义实际内核逻辑@T.prim_funcdef matmul_logic(A: T.Tensor((M, K), dtype),    # 输入矩阵AB: T.Tensor((K, N), dtype),    # 输入矩阵BC: T.Tensor((M, N), dtype),    # 输出矩阵C):# 3. 初始化内核上下文：定义网格和每块线程数# 使用每块128线程，通过N/block_N和M/block_M确定块数with T.Kernel(T.ceildiv(N, block_N), T.ceildiv(M, block_M), threads=128) as (bx, by):# 4. 分配快速本地内存(共享和片段)A_shared = T.alloc_shared((block_M, block_K), dtype)B_shared = T.alloc_shared((block_K, block_N), dtype)C_local = T.alloc_fragment((block_M, block_N), accum_dtype)# 5. 清空本地累加缓冲区T.clear(C_local)# 循环'K'维度(矩阵乘法的内维度)# 'ko'代表'K外部'块索引for ko in T.ceildiv(K, block_K):# 6. 将块从全局内存复制到共享内存# 每个块复制它需要的A和B块T.copy(A[by * block_M, ko * block_K], A_shared)T.copy(B[ko * block_K, bx * block_N], B_shared)# 7. 执行实际的块级矩阵乘法T.gemm(A_shared, B_shared, C_local)# 8. 将最终结果从本地片段复制到全局内存C# 使用T.Parallel在线程间分配复制任务for i, j in T.Parallel(block_M, block_N):C[by * block_M + i, bx * block_N + j] = C_local[i, j]return matmul_logic# --- 使用示例 ---
# 定义矩阵维度和块大小
M, N, K = 1024, 1024, 1024
block_M, block_N, block_K = 128, 128, 32# 1. 获取编译后的内核
my_matmul_kernel = matmul_kernel_builder(M, N, K, block_M, block_N, block_K)# 2. 用PyTorch准备输入张量(GPU数据)
a_torch = torch.randn(M, K, device="cuda", dtype=torch.float16)
b_torch = torch.randn(K, N, device="cuda", dtype=torch.float16)
c_torch = torch.empty(M, N, device="cuda", dtype=torch.float16) # 输出张量# 3. 运行TileLang内核
my_matmul_kernel(a_torch, b_torch, c_torch)print("TileLang内核输出(前5x5块)：")
print(c_torch[:5,:5])# 4. 与PyTorch参考对比验证正确性
ref_c_torch = a_torch @ b_torch # PyTorch原生矩阵乘法
torch.testing.assert_close(c_torch, ref_c_torch, rtol=1e-2, atol=1e-2)
print("\nTileLang内核输出与PyTorch参考匹配！")# `c_torch[:5,:5]`输出将是5x5的float16计算结果张量
# 如果结果数值相近，`assert_close`将通过

说明：这个完整示例展示了如何定义内核、指定内存分配、循环计算块、执行核心T.gemm操作，最后将结果复制回来

然后用PyTorch张量编译运行，对照PyTorch自身的torch.matmul验证正确性。

原理：T命名空间如何变为快速代码

当你使用T.copy或T.gemm等T命名空间函数时，实际上并非直接操作GPU的Python代码

而是在描述计算过程。TileLang记录这些描述，然后通过称为"编译"的过程，将其转换为针对GPU/CPU的高度优化机器指令。

可以这样理解：

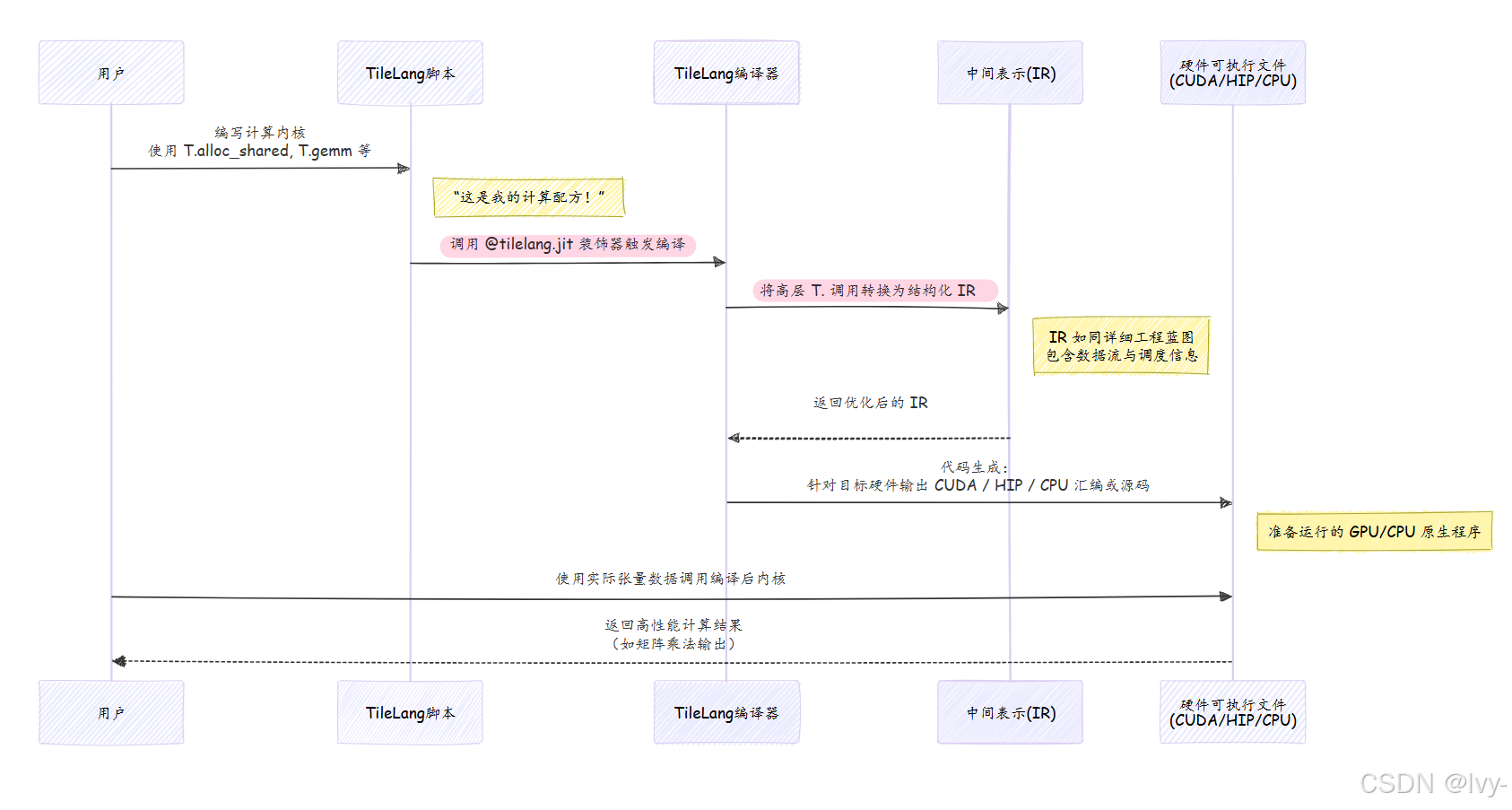
tilelang.language模块(通过import as T导入)充当桥梁

如果查看tilelang/language/__init__.py，会发现T.gemm、T.copy、T.Kernel等并非普通Python函数。它们是特殊构造，在T.prim_func内调用时会构建程序的内部表示(“配方”)。这个表示随后传递给强大的即时内核编译(JITKernel)系统，生成最终高效代码。

总结

本章中，已了解T命名空间是TileLang中编写高性能GPU/CPU内核的主要工具

它提供了Python风格的函数和构造，如T.Tensor用于数据定义、T.Kernel用于执行设置、T.alloc_shared/T.alloc_fragment用于内存管理、T.copy用于数据移动、T.Parallel用于并发执行，以及T.gemm等专门操作实现高效计算。

还通过实际示例学习了如何构建矩阵乘法内核，并理解了TileLang如何将高级Python描述编译为优化底层代码。

下一章我们将深入探索像T.gemm这样的超快操作如何工作，特别是它们如何利用Tensor Core等专用硬件特性。

第2章：张量核心操作(GEMM/WGMMA)