当前位置：首页 > news >正文

卫星几何处理

news 2025/10/16 6:32:58

卫星几何定位模型

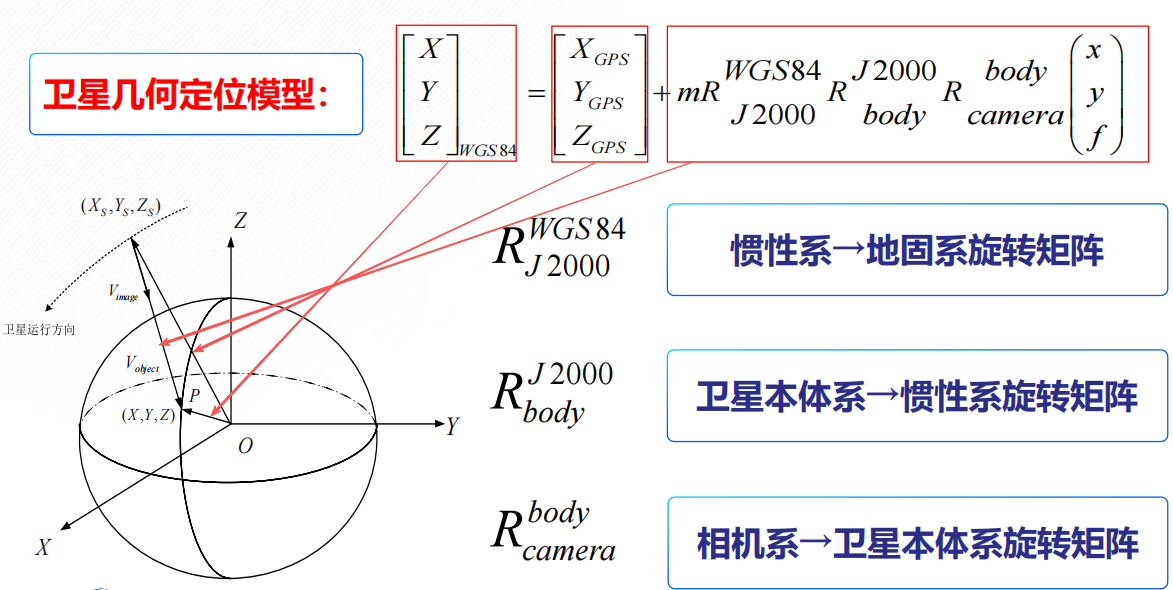
这实际上描述了一个空间几何关系：

📷 地面像点（X,Y,Z）在地心坐标系下的位置
＝ 卫星质心位置 + 卫星相机光线方向（在地固系下）× 比例因子 m

换句话说：

构建卫星影像像方二维坐标到物方三维坐标的物理模型，实现几何定位。
相机拍到的像素点，对应的光线（由相机坐标确定方向）经过多次坐标变换，被投影到地球表面，就得到该像素的地理位置

$[X_{GPS},Y_{GPS},Z_{GPS}]$

卫星质心在GPS下的坐标，这就是卫星在成像时刻的空间位置。由定轨结果提供

$(x, y , f)$

像点在相机坐标系下的坐标, 这定义了光线在相机坐标系下的方向向量。

x,y：像平面坐标（通常通过成像几何模型或相机内参获得）
f：焦距（相机主点到像平面的距离）

$R_{camera}^{body}$

这是相机坐标系 → 卫星机体坐标系的旋转矩阵，说明相机的安装姿态，例如相机光轴相对于卫星本体的俯仰、偏航、滚转角。由定标（外方位标定）确定

$R_{body}^{J2000}$

卫星机体坐标系 → 惯性坐标系（J2000）的旋转矩阵，这表示卫星在成像时的姿态（即卫星朝向哪儿拍）。由定姿结果（星敏感器、陀螺仪）给出

$R_{J2000}^{WGS84}$

惯性坐标系（J2000） → 地固坐标系（WGS-84）的旋转矩阵，与地球自转、岁差、章动有关
这是一个标准地球模型转换，由时间参数确定。

$m$

比例因子（或射线延伸系数），表示从相机出发沿光线方向延伸多远才能与地球相交。通过“相交地球椭球模型”求得。即确定光线与地球表面的交点。

定轨—定姿—定标

环节	对应参数	含义	数据来源
🛰️ 定轨	([X_{GPS}, Y_{GPS}, Z_{GPS}])	确定卫星在地固系下的位置	GPS / 星历数据
🔭 定姿	(R^{J2000}_{body})	确定卫星在惯性系中的姿态	星敏感器 / 陀螺仪
📷 定标	(R^{body}_{camera})，(f)，内参	描述相机相对卫星的安装误差	地面标定 / 实测
🌎 坐标变换	(R^{WGS84}_{J2000})	将惯性系姿态转换到地固系	地球模型计算
📍 地面定位	(m) 求解	光线与地球相交求交点	数值求解

卫星在轨道上（定轨） → 得到其在 WGS-84 系下的坐标
卫星姿态传感器（定姿） → 得到机体在 J2000 系中的朝向
相机安装矩阵（定标） → 得到相机相对机体方向
三个旋转矩阵连乘，将相机视线方向转到地固坐标系
光线方向 × 比例因子 m，加上卫星位置，就得地面点的坐标

基本坐标系

像平面坐标系：包括图像坐标系和焦面坐标系，描述像方点的二维坐标。

传感器坐标系：即相机坐标系，描述像方点的三维坐标。

卫星本体坐标系：基于整颗卫星构建的参考坐标系，星上各传感器的坐标基准

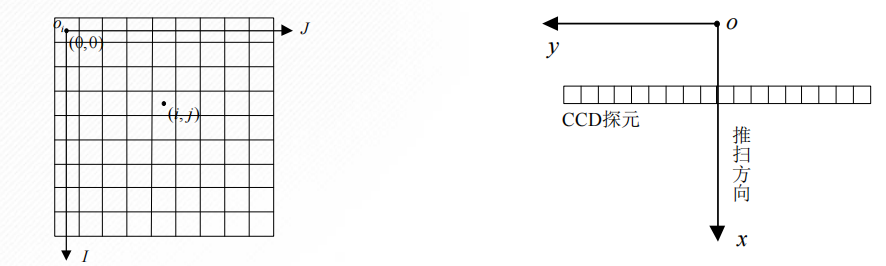
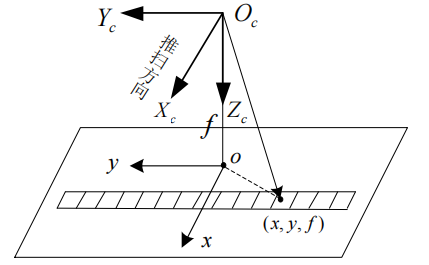
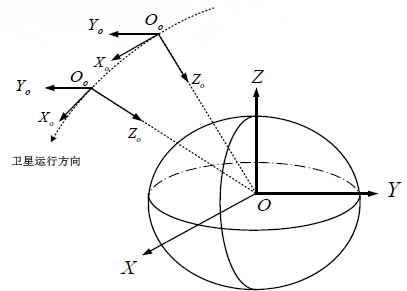
轨道坐标系：一种瞬时坐标系，多用于坐标之间的过渡、转换。

指向角模型

1. 起点：理想的严格物理模型

在理想情况下，我们使用针孔相机模型。一个像素 (x, y) 在相机坐标系中的方向向量是：
[x, y, f]^T

这个向量可以通过旋转和平移，转换到地球坐标系，从而进行定位。

2. 问题：现实世界的复杂性

现实中的相机远非理想：

镜头畸变：导致光线弯曲，使得实际像点位置 (x+Δx, y+Δy) 偏离理想位置 (x, y)。
探测器安装误差：探测器的阵列可能不是完美的平面，或者与光轴不完全垂直。
主点偏移：光轴与探测器平面的交点（主点）可能不在坐标原点 (0,0)，而在 (x₀, y₀)。

因此，第一个公式引入了这些修正：

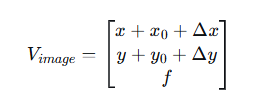
x, y：探元的理想坐标。
x₀, y₀：主点偏移。
Δx, Δy：由镜头畸变引起的修正量。
f：焦距。

这个模型虽然精确，但参数过多且耦合紧密（例如，主点偏移和某些畸变参数效应相似），导致在轨标定时非常困难，容易产生不稳定的解，这就是所谓的“过度参数化、无法精确标定”的问题。

3. 解决方案：指向角模型

为了规避上述问题，工程师们想出了一个更聪明的方法：绕过所有复杂的内部物理参数，直接测量和建模每个探元的最终输出——它在惯性空间中的指向角度。

演变的关键一步是归一化：
我们将方向向量除以焦距 f，得到一个新的向量，其Z分量为1：

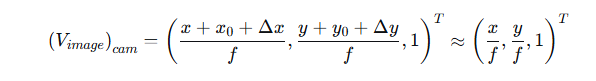
这个近似成立是因为 x₀, y₀, Δx, Δy 相对于 f 都是小量。这个向量的X和Y分量，在几何上恰好等于指向角正切值：

这里，ψₓ 和 ψ_y 就是指向角。

ψₓ：光线在X-Z平面上的投影与Z轴的夹角。
ψ_y：光线在Y-Z平面上的投影与Z轴的夹角。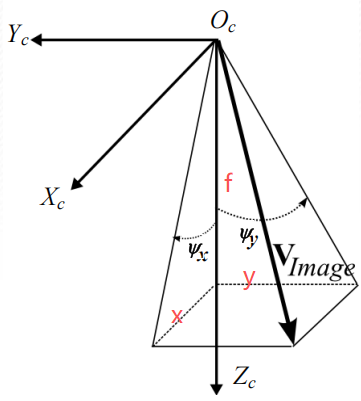

至此，我们成功地将问题从“求解一堆难以分离的内部几何参数”转变为了“直接为每个探元标定其唯一的指向角”。

核心模型公式

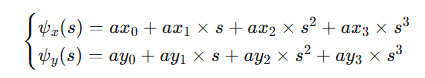
这个公式描述的是指向角随探元号变化的规律。

s (探元号)：
- 含义：探测器上每个敏感单元的编号。对于线阵推扫式卫星相机，这通常是从一端到另一端（例如，从0到11999）的序列号。
- 作用：自变量。模型认为，一个探元的指向角主要由它在探测器上的位置决定。
ψₓ(s), ψ_y(s)：
- 含义：探元号 s 所对应的探测单元，其光线的指向角。
- 单位：通常是弧度。
- 作用：因变量。这是我们最终要得到的量，用于构建几何定位模型。
多项式系数 ax₀, ax₁, ax₂, ax₃, ay₀, ay₁, ay₂, ay₃：
- 含义：描述指向角与探元号之间函数关系的系数。这里使用了一个三次多项式来拟合这种关系。
- 为什么是三次多项式？ 一次多项式（线性）只能描述均匀变化的视场；二次多项式可以描述对称的弯曲；三次多项式则能更好地拟合由于镜头畸变、探测器翘曲等引起的非对称、非线性的畸变。这在精度和复杂度之间取得了很好的平衡。
- 如何得到？ 这些系数是通过在轨几何定标来确定的。具体方法是：让卫星拍摄已知精确地理坐标的地面控制点，然后通过平差计算，反演出能使所有控制点投影误差最小的这一组系数。

工作流程与优势总结

定标阶段：
- 卫星对已知控制点区域成像。
- 通过平差算法，解算出一组最优的指向角模型系数 (ax₀...ax₃, ay₀...ay₃)。
- 这些系数被固化，作为相机参数的一部分。
定位阶段：
- 对于图像中的任何一个像素（其探元号为 s），代入指向角模型，直接计算出它的指向角 ψₓ(s) 和 ψy(s)。
- 根据 tan(ψₓ) 和 tan(ψ_y) 得到相机坐标系下的归一化方向向量 (tan(ψₓ), tan(ψy), 1)。
- 后续流程不变：利用卫星的姿态和轨道数据，将这个方向向量转换到地固坐标系，与卫星位置向量结合，通过共线方程解算出地面点的精确坐标。