当前位置：首页 > news >正文

《算法闯关指南：优选算法--二分查找》--19.x的平方根，20.搜索插入位置

news 2025/10/16 5:52:24

🔥草莓熊Lotso：个人主页

❄️个人专栏：《C++知识分享》《Linux 入门到实践：零基础也能懂》

✨生活是默默的坚持，毅力是永久的享受。

🎬博主简介：

前言：

19. x的平方根

解法（二分查找算法）：

算法思路：

C++算法代码：

算法总结&&笔记展示：

20. 搜索插入位置

解法（二分查找算法）：

算法思路：

C++算法代码：

算法总结&&笔记展示：

结尾：

前言：

聚焦算法题实战，系统讲解三大核心板块：优选算法：剖析动态规划、二分法等高效策略，学会寻找“最优解”。递归与回溯：掌握问题分解与状态回退，攻克组合、排列等难题。贪心算法：理解“局部最优”到“全局最优”的思路，解决区间调度等问题内容以题带点，讲解思路与代码实现，帮助大家快速提升代码能力。

19. x的平方根

题目链接：

69. x 的平方根 - 力扣（LeetCode）

题目描述：

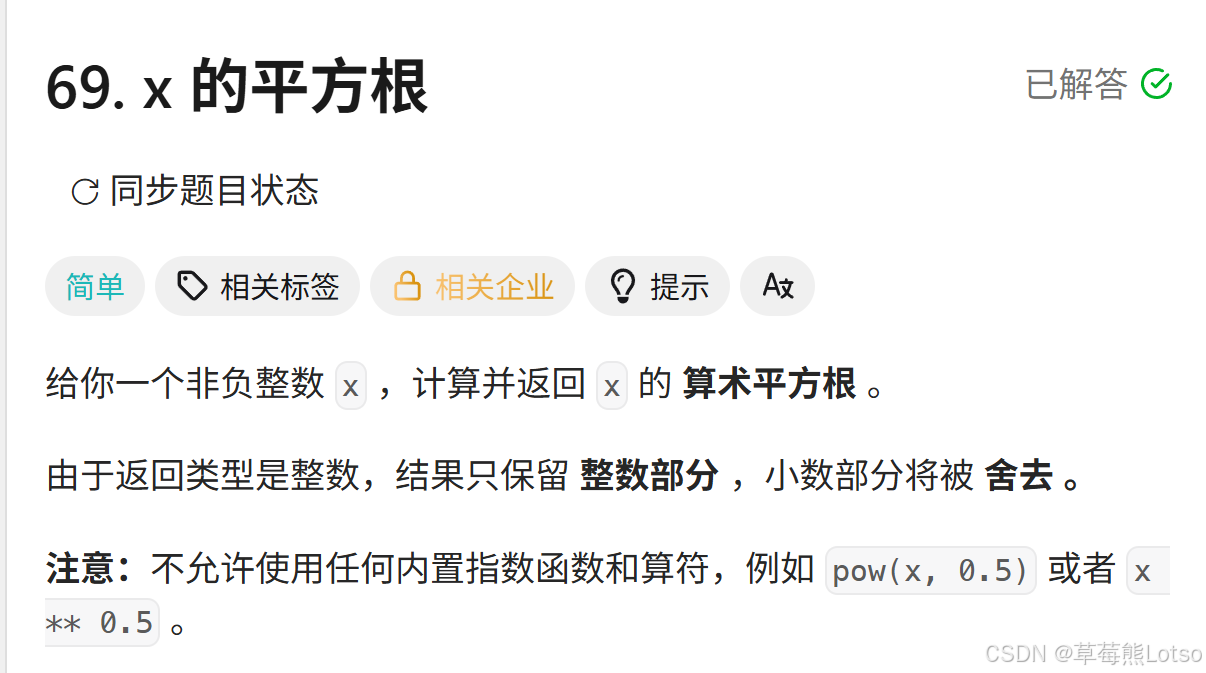
题目示例：

解法（二分查找算法）：

--暴力解法这里就不讲解了，只给大家看看代码

class Solution {
public:int mySqrt(int x) {// 由于两个较⼤的数相乘可能会超过 int 最⼤范围// 因此⽤ long longlong long i = 0;for (i = 0; i <= x; i++) {// 如果两个数相乘正好等于 x，直接返回 iif (i * i == x)return i;// 如果第⼀次出现两个数相乘⼤于 x，说明结果是前⼀个数if (i * i > x)return i - 1;}// 为了处理oj题需要控制所有路径都有返回值return -1;}
}

算法思路：

设 x 的平方根的最终结果为 index：

分析 index 左右两边数据的特点：

【0，index】之间的元素，平方之后都小于等于 x；
【index+1，x】之间的元素，平方之后都大于 x；

因此可以使用二分查找算法

C++算法代码：

class Solution {
public:int mySqrt(int x) {if(x<1) return 0;int left=1,right=x;while(left<right){long long mid=left+(right-left+1)/2;if(mid*mid<=x) left=mid;else right=mid-1;}return left;}
};

算法总结&&笔记展示：

笔记字有点丑，大家见谅：

20. 搜索插入位置

题目链接：

35. 搜索插入位置 - 力扣（LeetCode）

题目描述：

题目示例：

解法（二分查找算法）：

算法思路：

分析插入位置左右两侧区间上元素的特点：设插入位置的坐标为 index

【left，index-1】内所有元素均是小于 target 的；
【index，right】内所有元素均是大于等于 target 的

设 left 为本轮查询的左边界，right 为本轮查询的右边界，根据 mid 位置元素的信息，分析下一轮查询的区间：

当 nums[mid] >= target 时，说明 mid 落在了 [index, right] 区间上，mid 左边包括 mid 本身，可能是最终结果，所以我们接下来查找的区间在 [left, mid] 上。因此，更新 right 到 mid 位置，继续查找。
当 nums[mid] < target 时，说明 mid 落在了 [left, index - 1] 区间上，mid 右边但不包括 mid 本⾝，可能是最终结果，所以我们接下来查找的区间在 [mid+ 1, right] 上。因此，更新 left 到 mid + 1 的位置，继续查找。

直到我们的查找区间的长度变为 1 ，也就是 left == right 的时候， left 或者 right 所在的位置就是我们要找的结果。

C++算法代码：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}if(nums[left]<target) return left+1;return left;}
};