从中序与后序遍历序列构造二叉树
以下内容是从网站中学习的,如果有错误欢迎批评指正~~
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
- 中序遍历 inorder = [9,3,15,20,7]
- 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树:
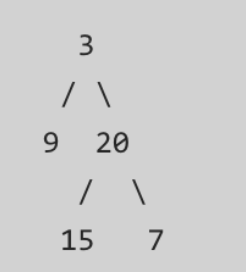
思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:
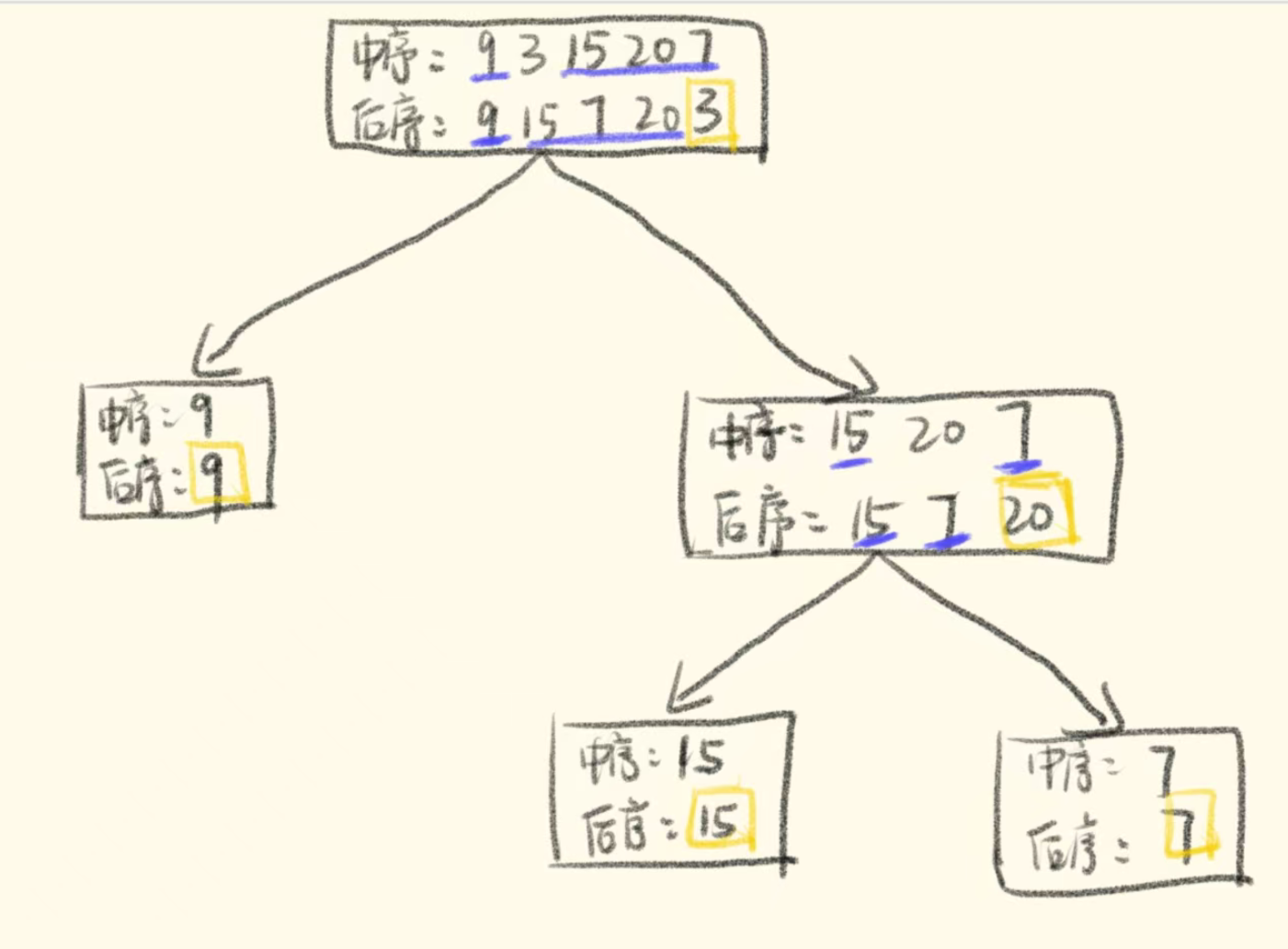
那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
我在二分法和数组循环中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,本题坚持左闭右开的原则。
接下来就要切割后序数组了。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
接下来可以递归了,
//106.从中序与后序遍历序列构造二叉树class Solution{Map<Integer,Integer> map;//方便根据数值查找位置public TreeNode buildTree(int[] inorder,int[] postorder){map = new HashMap<>();for(int i = 0;i < inorder.length;i++){//用map保存中序序列的数值对应位置map.put(inorder[i],i);}return findNode(inorder,0,inorder.length,postorder,0,postorder.length); //前闭后开}public TreeNode findNode(int [] inorder,int inBegin,int inEnd,int [] postorder,int postBegin,int postEnd){//参数里的范围都是前闭后开if(inBegin >= inEnd || postBegin >= postEnd){ // 不满足左闭右开,说明没有元素,返回空树return null;}int rootIndex = map.get(postorder[postEnd - 1]);//找到后序遍历的最后一个元素在中序遍历中的位置TreeNode root = new TreeNode(inorder[rootIndex]);//构造节点int lenOfLeft = rootIndex - inBegin;//保存中序左子树个数,用来确定后序数列的个数root.left = findNode(inorder,inBegin,rootIndex,postorder,postBegin,postBegin + lenOfLeft);root.right = findNode(inorder,rootIndex + 1,inEnd,postorder,postBegin + lenOfLeft,postEnd - 1);return root;}}相关题目推荐
从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树:
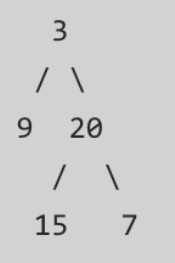
思路
本题和106是一样的道理。
我就直接给出代码了。
class Solution {Map<Integer, Integer> map;public TreeNode buildTree(int[] preorder, int[] inorder) {map = new HashMap<>();for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置map.put(inorder[i], i);}return findNode(preorder, 0, preorder.length, inorder, 0, inorder.length); // 前闭后开}public TreeNode findNode(int[] preorder, int preBegin, int preEnd, int[] inorder, int inBegin, int inEnd) {// 参数里的范围都是前闭后开if (preBegin >= preEnd || inBegin >= inEnd) { // 不满足左闭右开,说明没有元素,返回空树return null;}int rootIndex = map.get(preorder[preBegin]); // 找到前序遍历的第一个元素在中序遍历中的位置TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数,用来确定前序数列的个数root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,inorder, inBegin, rootIndex);root.right = findNode(preorder, preBegin + lenOfLeft + 1, preEnd,inorder, rootIndex + 1, inEnd);return root;}
}思考
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢?
前序和后序不能唯一确定一棵二叉树!,因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
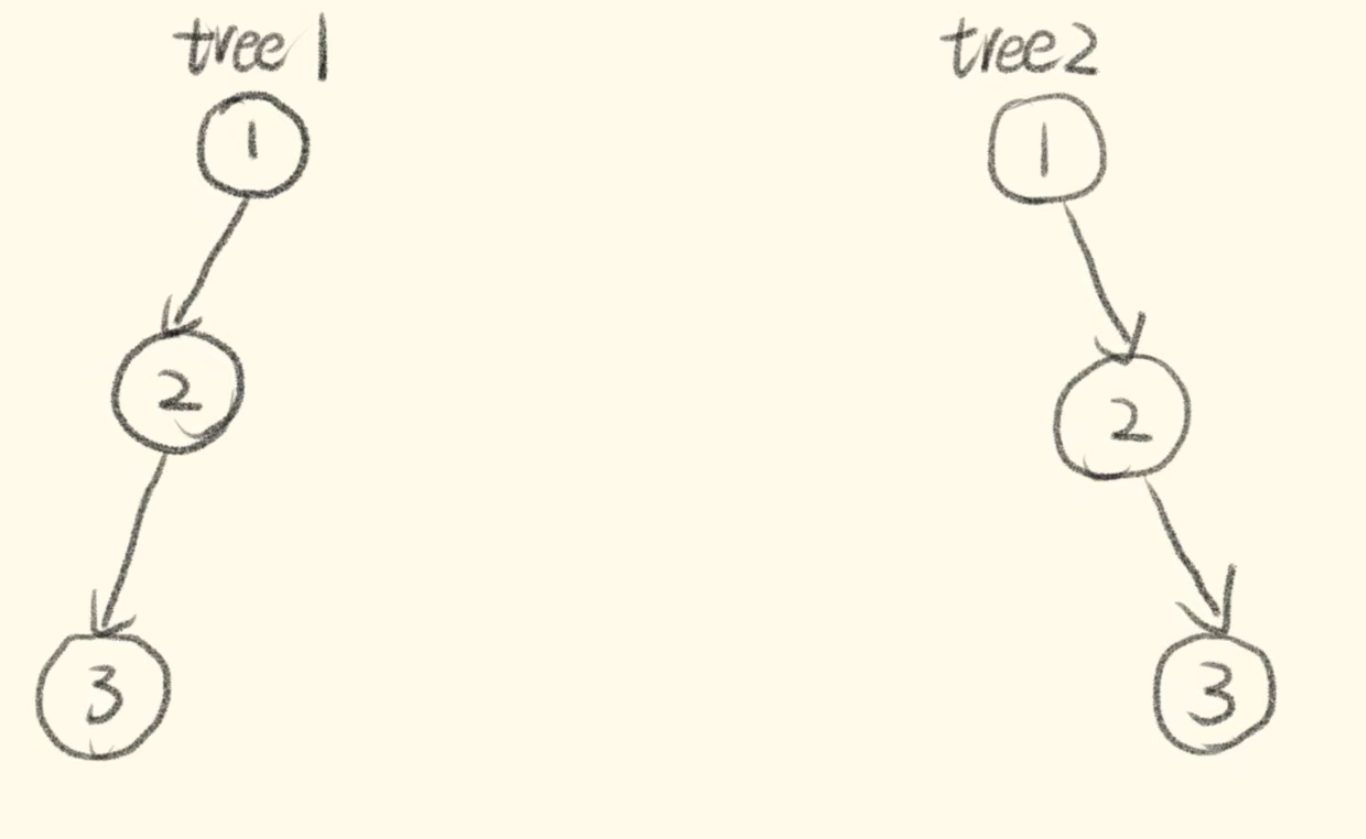
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树!
总结
之前我们讲的二叉树题目都是各种遍历二叉树,这次开始构造二叉树了,思路其实比较简单,但是真正代码实现出来并不容易。
所以要避免眼高手低,踏实地把代码写出来。
我同时给出了添加日志的代码版本,因为这种题目是不太容易写出来调一调就能过的,所以一定要把流程日志打出来,看看符不符合自己的思路。
大家遇到这种题目的时候,也要学会打日志来调试(如何打日志有时候也是个技术活),不要脑动模拟,脑动模拟很容易越想越乱。
最后我还给出了为什么前序和中序可以唯一确定一棵二叉树,后序和中序可以唯一确定一棵二叉树,而前序和后序却不行。
认真研究完本篇,相信大家对二叉树的构造会清晰很多。
