基于成功率的自适应差分进化 L-SRTDE 用于 CEC 2024 竞赛
Success Rate-based Adaptive Differential Evolution L-SRTDE for CEC 2024 Competition
摘要(Abstract)
差分进化算法最重要的问题之一是对缩放因子的自适应调整,因为算法性能对该参数高度敏感。本文提出了 L-SRTDE 算法,其中缩放因子根据每一代中改进解的比率(即成功率)来设定。所提出的算法用于求解 CEC 2024 有界约束单目标数值优化竞赛中的基准问题。还使用 CEC 2017 和 CEC 2022 基准进行了额外的实验。对数值结果的分析(同时考虑了算法的精度和速度)表明,所提出的方法能够胜过许多使用基于成功历史自适应的替代方法。
关键词:差分进化,数值优化,参数自适应
I 引言(INTRODUCTION)
针对黑盒场景的全局数值优化方法的开发是一个重要的研究方向,因为此类问题出现在许多行业和研究中。差分进化 [1] 是一种流行的启发式优化方法,以其简单性和高效性而闻名。关于 DE 的大量研究涉及不同方面,例如新的变异策略、交叉操作、种群大小控制和参数自适应 [2]。
本研究的重点在于参数自适应方法,并选择最近提出的 L-NTADE 算法作为基线 [3]。这里,最初在 SHADE 算法 [4] 中提出的基于成功历史的自适应被替换为针对缩放因子 F 的基于成功率的自适应。成功率 SR 被定义为改进解的数量与当前种群大小的比率。除了自适应缩放因子外,r-new-to-ptop/nt 变异策略中的贪婪参数 pb 也由成功率控制。成功率与缩放因子之间的联系先前已通过使用遗传编程的超启发式方法 [5] 发现,并在 [6] 中通过应用泰勒级数进行了进一步研究。
使用进化计算大会(CEC)2017 [7] 和 CEC 2022 [8] 基准对新提出的 L-SRTDE(线性种群大小缩减基于成功率的差分进化)进行的实验表明,在使用相同参数集的情况下,它能够胜过大多数已知算法。还对 CEC 2024 基准 [9] 进行了实验,该基准使用了 CEC 2017 的 30 维函数,以及不同的解评估技术。
本文的其余部分组织如下。下一节简要介绍 DE 及相关工作。第三节详细描述了 L-SRTDE。第四节包含实验设置和结果,第五节对全文进行总结。
II 相关工作(RELATED WORK)
DE 的主要特征之一是其能够通过搜索空间中向量的分布隐式地适应问题的地形。在几乎任何 DE 变体中,在随机初始化和评估解之后,开始变异步骤,这是任何 DE 变体的关键组成部分。它允许利用存储在向量位置中的信息。最流行的变异策略之一是 JADE [10] 中提出的 current-to-pbest,并进一步用于 SHADE [4] 及其衍生的算法中:
v i , j = x i , j + F ( x p b e s t , j − x i , j ) + F ( x r 1 , j − x r 2 , j ) . (1) v_{i,j}=x_{i,j}+F(x_{pbest,j}-x_{i,j})+F(x_{r1,j}-x_{r2,j}).\tag{1} vi,j=xi,j+F(xpbest,j−xi,j)+F(xr1,j−xr2,j).(1)
其中 x i x_{i} xi 是包含 N N N 个个体的种群中的第 i i i 个向量,每个向量由 D D D 个变量组成, v i v_{i} vi 称为供体向量, r 1 r1 r1 和 r 2 r2 r2 是来自种群的随机索引, p b e s t pbest pbest 是前 p % p\% p% 最佳个体之一, F F F 是变异参数, i = 1 , 2 , . . . N i=1,2,...N i=1,2,...N, j = 1 , 2 , . . . D j=1,2,...D j=1,2,...D。current-to-pbest 策略包含两个组成部分:开发(即收敛到前 p % p\% p% 最佳解之一)体现在第一个差分向量中,探索(在随机方向上的步骤)体现在第二个差分向量中。通过这种方式,DE 能够平衡这两种趋势。
变异之后,在供体向量 v i v_{i} vi 和目标向量 x i x_{i} xi 之间执行交叉步骤以产生试验向量 u i u_{i} ui。大多数 DE 算法依赖于二项式交叉:
u i , j = { v i , j , i f r a n d ( 0 , 1 ) ≤ C r o r j = j r a n d x i , j , o t h e r w i s e . (2) u_{i,j}=\begin{cases}v_{i,j},&if \ rand(0,1)\leq Cr \ or\ j=jrand\\ x_{i,j},&otherwise\end{cases}.\tag{2} ui,j={vi,j,xi,j,if rand(0,1)≤Cr or j=jrandotherwise.(2)
这里 j r a n d jrand jrand 用于确保至少有一个分量来自供体向量, C r Cr Cr 是交叉率参数。尽管二项式交叉是最流行的,但一些研究也实现了指数交叉 [11] 甚至特征变换 [12]。试验向量也通过边界约束处理方法进行处理,例如中点目标法或重采样法 [13]。
评估新解后,应用选择步骤。DE 选择是目标向量和试验向量的简单比较:
x i , j = { u i , j , i f f ( u i ) ≤ f ( x i ) x i , j , i f f ( u i ) > f ( x i ) . (3) x_{i,j}=\begin{cases}u_{i,j},&if \ f(u_{i})\leq f(x_{i})\\ x_{i,j},&if\ f(u_{i})>f(x_{i})\end{cases}.\tag{3} xi,j={ui,j,xi,j,if f(ui)≤f(xi)if f(ui)>f(xi).(3)
A.DE 中的参数自适应(Parameter adaptation in DE)
差分进化的简单性带来了一定的代价:该算法对三个主要参数高度敏感:种群大小 N N N、缩放因子 F F F 和交叉率 C r Cr Cr。缩放因子起着至关重要的作用,对 DE 的性能影响最大。一些早期研究 [14] 提出了设置控制参数的建议,例如 F > 0.4 F>0.4 F>0.4,然而,固定值已被证明效率低下。因此,自适应算法被开发出来,例如 SaDE [15] 和 jDE [16]。在 jDE 中, F F F 的值在 [ 0.1 , 0.9 ] [0.1,0.9] [0.1,0.9] 范围内采样, C r Cr Cr 在 [ 0 , 1 ] [0,1] [0,1] 范围内采样,如果发生改进,则保存新值。
尽管 jDE 方法被证明具有竞争力 [17][18],但大多数关于 DE 的工作使用基于成功历史的自适应 [4]。SHA 设置 H H H 个存储单元,包含 M F , k M_{F,k} MF,k 和 M C r , k M_{Cr,k} MCr,k 参数,分别用于后续使用柯西分布和正态分布进行采样: F = r a n d c ( M F , h , 0.1 ) F=randc(M_{F,h},0.1) F=randc(MF,h,0.1), C r = r a n d n ( M C r , h , 0.1 ) Cr=randn(M_{Cr,h},0.1) Cr=randn(MCr,h,0.1), h h h 在 [ 1 , H ] [1,H] [1,H] 中随机选择。在选择过程中,成功的 F F F 和 C r Cr Cr 值连同适应度改进量 S Δ f = f ( x i ) − f ( u i ) S_{\Delta f}=f(x_{i})-f(u_{i}) SΔf=f(xi)−f(ui) 被保存到 S F S_{F} SF 和 S C r S_{Cr} SCr 中。在每一代结束时,计算两个加权 Lehmer 均值:
m e a n w L , F = ∑ j = 1 ∣ S F ∣ w j S F , j 2 ∑ j = 1 ∣ S F ∣ w j S F , j , m e a n w L , C r = ∑ j = 1 ∣ S C r ∣ w j S C r , j 2 ∑ j = 1 ∣ S C r ∣ w j S C r , j (4) mean_{wL,F}=\frac{\sum_{j=1}^{|S_{F}|}w_{j}S^{2}_{F,j}}{\sum_{j=1}^{|S_{F}|}w_{j} S_{F,j}},\\ mean_{wL,Cr}=\frac{\sum_{j=1}^{|S_{Cr}|}w_{j}S^{2}_{Cr,j}}{\sum_{j=1}^{|S _{Cr}|}w_{j}S_{Cr,j}} \tag{4} meanwL,F=∑j=1∣SF∣wjSF,j∑j=1∣SF∣wjSF,j2,meanwL,Cr=∑j=1∣SCr∣wjSCr,j∑j=1∣SCr∣wjSCr,j2(4)
其中 w j = S Δ f , j ∑ k = 1 ∣ S ∣ S Δ f , k w_{j}=\frac{S_{\Delta f,j}}{\sum_{k=1}^{|S|}S_{\Delta f,k}} wj=∑k=1∣S∣SΔf,kSΔf,j 。此后,更新索引为 k k k 的存储单元之一(该索引每代迭代):
{ M F , k g + 1 = 0.5 ⋅ ( M F , k g + m e a n ( w L , F ) ) M C r , k g + 1 = 0.5 ⋅ ( M C r , k g + m e a n ( w L , C r ) ) , (5) \begin{cases}M^{g+1}_{F,k}=0.5\cdot\left(M^{g}_{F,k}+mean_{(wL,F)}\right)\\ M^{g+1}_{Cr,k}=0.5\cdot\left(M^{g}_{Cr,k}+mean_{(wL,Cr)}\right)\end{cases},\tag{5} ⎩ ⎨ ⎧MF,kg+1=0.5⋅(MF,kg+mean(wL,F))MCr,kg+1=0.5⋅(MCr,kg+mean(wL,Cr)),(5)
其中 g g g 是当前代数。如果 k > H k>H k>H,则将其设置为 k = 1 k=1 k=1。
基于成功历史的自适应遵循目标函数的即时改进来调整两个主要参数 F F F 和 C r Cr Cr。在 [19] 中表明,增加 Lehmer 均值中的偏置参数可能是有益的,因为 SHA 倾向于设置比更好性能所需更小的值,因此这种自适应方法可以被称为贪婪的。
对于第三个主要参数,种群大小 N N N,已经提出了几种控制策略。在 [20] 中提出了线性种群大小缩减(LPSR),它通过在开始时更好地覆盖搜索空间并在结束时将搜索集中在最有希望的区域,显著提高了性能。在 [11] 中使用了 LPSR 的修改,特别是种群大小缩减得更快。
SHADE [4] 算法的另一个特点是使用外部存档 A A A。在选择步骤中,被新解替换的解不会被删除,而是被发送到存档中,存档大小有限(例如 ∣ A ∣ = 2 ⋅ N |A|=2\cdot N ∣A∣=2⋅N)。一旦存档填满,其解将被随机替换。存档的解随后在变异步骤中使用,其中 r 2 r2 r2 索引从种群和存档的联合集合中选择。
B.DE 的改进(DE modifications)
对 DE 的研究不仅限于参数自适应。在 [21] 中提出了基于排序的选择,并在 [22] 中用于 L-SHADE-RSP 算法,其中 current-to-pbest 变异策略的索引是根据相应个体的适应度值相关的概率选择的。为此,对个体进行排序和排名,分配的排名如下:
r a n k i = e − k p ⋅ i N (6) rank_{i}=e^{\frac{-kp\cdot i}{N}}\tag{6} ranki=eN−kp⋅i(6)
其中 k p kp kp 是选择压力参数, i = 1 , 2 , . . . N i=1,2,...N i=1,2,...N。选择压力被证明可以提高收敛速度,特别是在高维情况下。
在 [23] 中,研究了具有无限种群大小的差分进化,其中所有先前的解都被保存。研究表明,应用不同的选择策略可能会带来显著的性能优势。受这项研究的启发,在 [3] 中提出了 L-NTADE 算法。
L-NTADE 算法有两个种群:一个用于最新解 x n e w x^{new} xnew,另一个用于顶级解 x t o p x^{top} xtop,具有相同的大小 N N N。在初始化时,两个种群都填充相同的解。变异策略称为 r-new-to-ptop/nt,工作方式如下:
v i , j = x r 1 , j n e w + F ⋅ ( x p b e s t , j t o p − x i , j n e w ) + F ⋅ ( x r 2 , j n e w − x r 3 , j t o p ) (7) v_{i,j}=x^{new}_{r1,j}+F\cdot(x^{top}_{pbest,j}-x^{new}_{i,j})+F\cdot(x^{new}_ {r2,j}-x^{top}_{r3,j})\tag{7} vi,j=xr1,jnew+F⋅(xpbest,jtop−xi,jnew)+F⋅(xr2,jnew−xr3,jtop)(7)
其中 r 1 r1 r1 和 r 3 r3 r3 是随机选择的, r 2 r2 r2 是通过基于排序的选择压力( k p = 3 kp=3 kp=3)选择的, p b e s t pbest pbest 是从顶级种群中前 p b % pb\% pb% 的最佳解中选择的。与 current-to-pbest 不同,该策略使用随机选择的解 x r 1 n e w x^{new}_{r1} xr1new 作为基础向量,而不是目标向量。
L-NTADE 中的交叉和边界约束处理是经典的,但选择步骤有显著不同,工作方式如下:
x n c = { u i , i f f ( u i ) ≤ f ( x r 1 n e w ) x n c , i f f ( u i ) > f ( x r 1 n e w ) . (8) x_{nc}=\begin{cases}u_{i},& if\ f(u_{i})\leq f(x^{new}_{r1})\\ x_{nc},&if\ f(u_{i})>f(x^{new}_{r1})\end{cases}.\tag{8} xnc={ui,xnc,if f(ui)≤f(xr1new)if f(ui)>f(xr1new).(8)
其中 n c nc nc 是一个索引,在每次成功替换后迭代,如果 n c > N nc>N nc>N 则重置为 1 1 1。试验向量 u i u_{i} ui 与基础向量 x r 1 n e w x^{new}_{r1} xr1new 进行比较,如果试验向量更好,则它替换索引为 n c nc nc 的个体,而不是索引 i i i 的个体。这导致 x n e w x^{new} xnew 种群不断用最新解更新,尽管更好的向量可能被更差的向量替换。此外,所有成功的向量及其适应度值都存储在一个临时池 x t e m p x^{temp} xtemp 中。在每一代结束时,最佳解种群 x t o p x^{top} xtop 与 x t e m p x^{temp} xtemp 合并,按适应度排序,并将最好的 N N N 个解( N N N 根据 LPSR 重新计算)放入 x t o p x^{top} xtop。因此,顶级种群始终包含迄今为止最好的 N N N 个解。
L-NTADE 算法被证明与经典 DE 方案有显著不同,并且在多种场景下表现更好。然而,它仍然依赖于成功历史自适应来设置 F F F 和 C r Cr Cr。在 [5] 中,应用遗传编程算法为 L-NTADE 自动生成参数自适应启发式规则,遵循超启发式(HH)范式 [24]。研究发现,选择中改进解的比率(即成功率)与缩放因子 F F F 的设置有很强的联系。当前的研究基于这些发现,以及 [6] 中曲线搜索的实验,并提出了 L-SRTDE 算法,在下一节中描述。
III 提出的方法:L-SRTDE
下面描述的方法基于在 [25] 中进行的关于参数自适应方法的超启发式搜索实验。L-SRTDE 算法是 L-NTADE 的一个修改版本,具有两个主要特点。首先,缩放因子自适应 F F F 基于成功率,用于采样的均值设置如下:
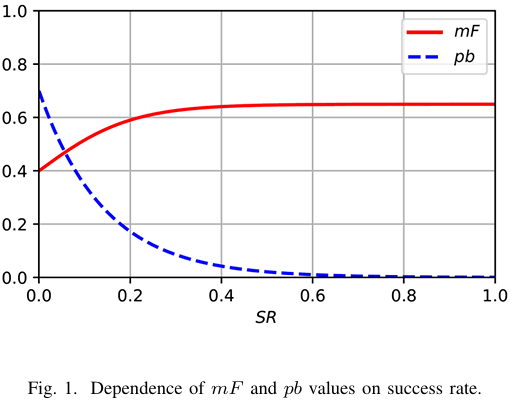
m F = 0.4 + 0.25 ⋅ t a n h ( 5 ⋅ S R ) (9) mF=0.4+0.25\cdot tanh(5\cdot SR)\tag{9} mF=0.4+0.25⋅tanh(5⋅SR)(9)
其中 S R = N S N SR=\frac{NS}{N} SR=NNS, N S NS NS 是成功解的数量,即选择操作起作用的次数,tanh为双曲正切函数。然后使用 m F mF mF 值对每个变异的 F F F 值进行采样,即 F = r a n d n ( m F , 0.02 ) F=randn(mF,0.02) F=randn(mF,0.02)。所描述的依赖性是通过类似于 [6] 中使用的超启发式方法找到的。
第二个修改使用成功率来设置变异策略的 p b pb pb 参数。依赖性如下:
p b = 0.7 ⋅ e − 7 ⋅ S R (10) pb=0.7\cdot e^{-7\cdot SR}\tag{10} pb=0.7⋅e−7⋅SR(10)
也就是说,如果成功率接近 0,则 pbest 索引从前 70 % 70\% 70% 的最佳解中选择,这接近于随机选择。然而,随着成功率的增长, p b pb pb 减小,并更集中于更少数量的最佳解。注意,即使 p b ⋅ N < 2 pb\cdot N<2 pb⋅N<2,pbest 索引也从两个最佳解中选择一个,即 p b e s t = r a n d i ( m a x ( 2 , p b ⋅ N ) ) pbest=randi(max(2,pb\cdot N)) pbest=randi(max(2,pb⋅N)),其中 r a n d i ( m ) randi(m) randi(m) 是从 1 1 1 到 m m m 的随机整数。
L-SRTDE 中的另一个小修改是使用了 [26] 中描述的修复交叉率。不是使用为交叉采样的交叉率 C r Cr Cr,而是计算实际的 C r a Cr_{a} Cra 值,即替换分量的数量除以维度 D D D。在这种情况下,在自适应过程中 M C r , h M_{Cr,h} MCr,h 永远不会变为 0 0 0,并至少保持在 1 / D 1/D 1/D。对于 C r Cr Cr 自适应,L-SRTDE 中使用 SHA,并且值以较小的离散度采样: C r = r a n d n ( M C r , k , 0.05 ) Cr=randn(M_{Cr,k},0.05) Cr=randn(MCr,k,0.05)。
图 1 显示了描述 m F mF mF 和 p b pb pb 值对成功率的依赖关系的曲线。
算法1中给出了L-SRTDE的完整伪代码。

下一节包含实验设置和数值结果。
IV 实验与结果(EXPERIMENTS AND RESULTS)
CEC 2024 [9] 单目标有界约束数值优化基准基于 CEC 2017 [7],并使用 30 维情况。测试集包含 29 个不同的函数,包括单峰、多峰、混合和复合函数。与 2017 年竞赛不同,在 CEC 2024 中,不仅考虑最佳目标函数值,还考虑达到最优解(精度为 1 0 − 8 10^{-8} 10−8)所需的函数评估次数。CEC 2022 竞赛 [8] 也使用了相同的方法。为了比较目的,使用了 U-score 排名方法 [27],其中应用了成对 Mann-Whitney U 检验。除此之外,还应用了标准的 Mann-Whitney 检验和 Friedman 排序程序。
CEC 2017 和 2024 基准的计算资源设置为 10000 ⋅ D 10000\cdot D 10000⋅D 次评估,对于 CEC 2022,10 D D D 设置为 2 ⋅ 1 0 5 2\cdot 10^{5} 2⋅105,20 D D D 设置为 1 0 6 10^{6} 106。独立运行次数对于 CEC 2017 为 51 次,对于 CEC 2022 为 30 次,对于 CEC 2024 为 25 次。为了与其他方法进行适当比较,在三个基准上测试 L-SRTDE 时,应用了相应的规则。
L-SRTDE 的参数设置如下:初始种群大小 N = 20 D N=20D N=20D,最小种群大小 N m i n = 4 N_{min}=4 Nmin=4,存储单元数量 H = 5 H=5 H=5,存储单元中的初始值 M C r , k = 1 M_{Cr,k}=1 MCr,k=1,选择压力参数 k p = 3 kp=3 kp=3。这些值在基准测试之间没有改变。L-SRTDE 算法在 C++ 中实现,使用 GCC 编译,并在配备 AMD Ryzen 5800X 处理器的 Ubuntu 20.04 机器上运行。结果后处理、排序和统计检验使用 Python 3.8 进行。
A.CEC 2017 比较(CEC 2017 comparison)
在第一组实验中,将 L-SRTDE 与 CEC 2017 和 2018 竞赛中的几种算法进行了比较。使用了正态近似(使用 Z-score 计算)和处理平局的 Mann-Whitney U 检验,结果显示在表 I 中。显著性水平设置为 p = 0.01 p=0.01 p=0.01。表中的数字是胜/平/负的数量。另外给出了总的标准化 Z 分数。这些比较中未考虑收敛速度。
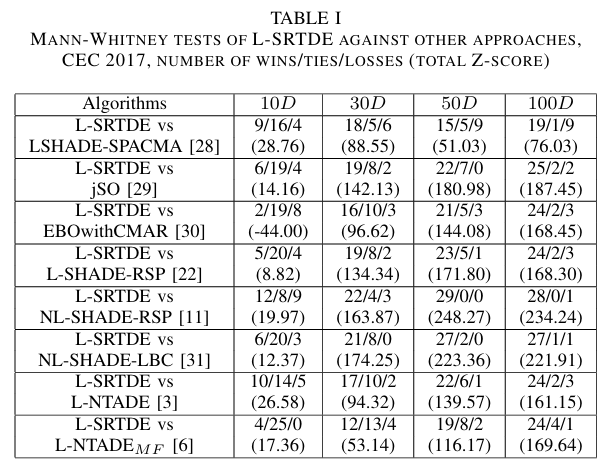
如表 I 所示,L-SRTDE 仅在一种情况下失败,即在 10 D D D 时输给了 EBOwithCMAR 算法。但在 30 D D D 时,它的表现更好,并且性能差异随着维度的增加而增大。与基线算法 L-NTADE 相比,L-SRTDE 在大多数情况下表现更好,并且差异随着维度的增加而增大。表 II 包含了比较中所有算法的 Friedman 排序。
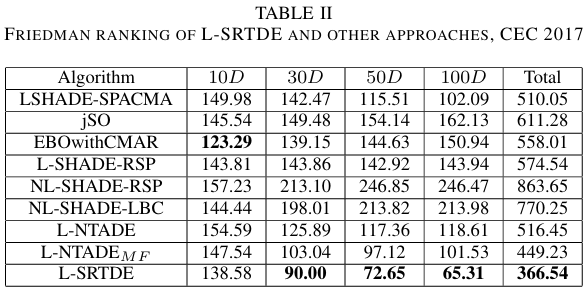
表 II 中的结果显示了类似的趋势,在 10 D D D 情况下,所有方法的得分相似,EBOwithCMAR 最好。在 30 D D D 及更高维度情况下,L-SRTDE 占据领先位置。表 III 包含了 U-scores 比较。
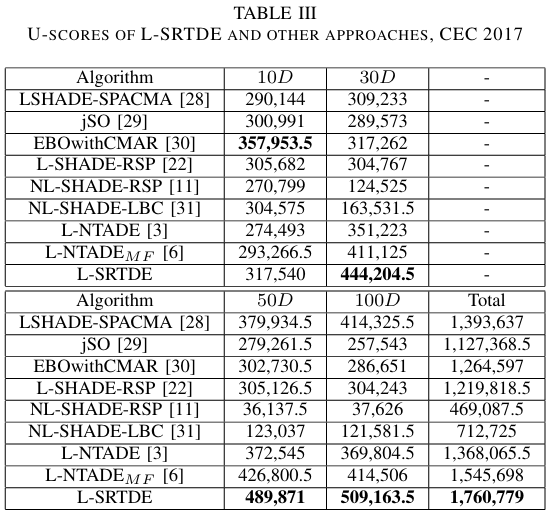
表 III 中呈现的 U-scores 展示了类似的结果,在更高维情况下,L-SRTDE 的表现优于任何其他算法。此外,作为 CEC 2021 竞赛获胜者的 NL-SHADE-RSP 算法在 50 D D D 和 100 D D D 情况下显示出最差的结果之一,而 L-SHADE-RSP 在所有维度上都具有大约 304-305 千的稳定得分。
B.CEC 2022 比较(CEC 2022 comparison)
为了与 CEC 2022 基准进行比较,选取了竞赛中的顶级算法。这里,在统计检验的所有排序和排名中,收敛速度均按照 [8] 中描述的方式予以考虑。表 IV 包含了 Mann-Whitney 成对检验。
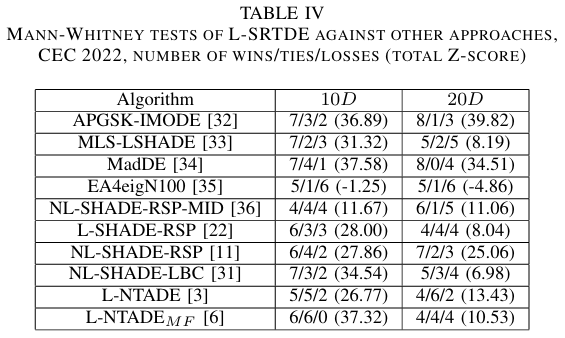
如表 IV 所示,L-SRTDE 在 10 D 10D 10D 和 20 D 20D 20D 情况下均输给了 CEC 2022 的获胜者 EA4eigN100 算法,结果为 5 胜 1 平 6 负。与其他方法相比,L-SRTDE 更好,尽管在 20 D 20D 20D 情况下优势较小。表 V 和 VI 包含了 Friedman 排序和 U-scores。
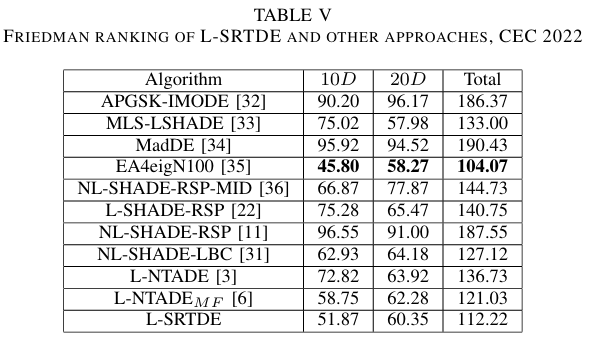
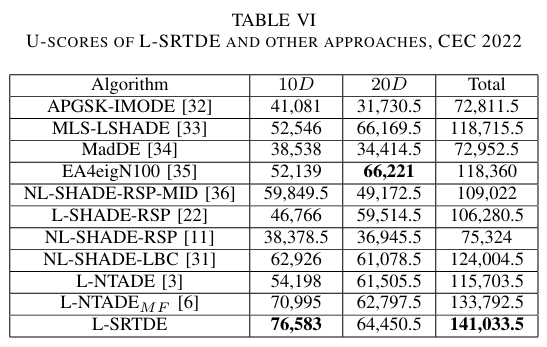
与 CEC 2017 基准不同,在 CEC 2017 中 Friedman 排序和 U-scores 得出相似结论,而表 V 显示 EA4eigN100 是整体最佳算法,L-SRTDE 次之,但表 VI 显示 L-SRTDE 在 10 D 10D 10D 中是最好的方法,在 20 D 20D 20D 中排名第三,EA4eigN100 和 MLS-LSHADE 更好。这表明结论可能因比较方法而异。
C.CEC 2024 比较(CEC 2024 comparison)
为了在 CEC 2024 竞赛的新设置下比较不同算法,我们对几种源代码可用的算法进行了评估。表 VII、VIII 和 IX 包含了 10 D 10D 10D 和 30 D 30D 30D 情况的 Mann-Whitney 检验、Friedman 排序和 U-scores。
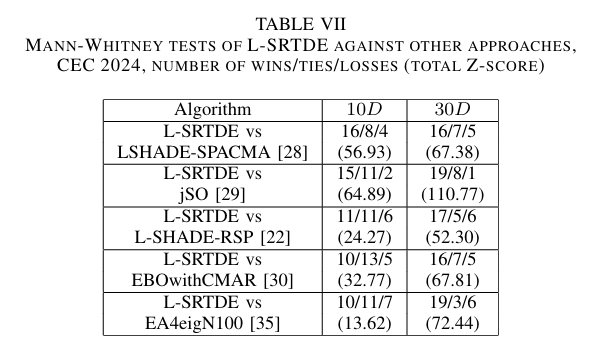
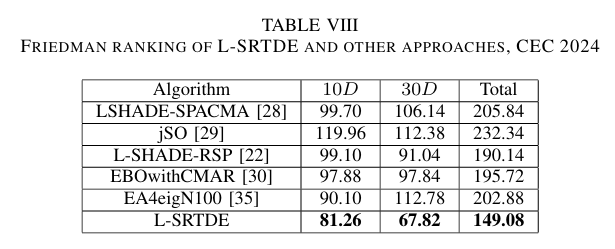
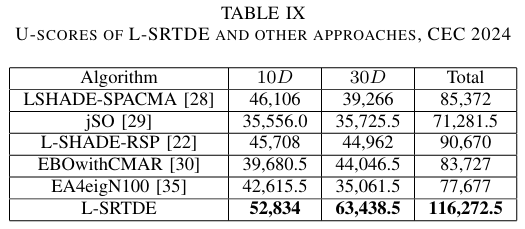
表 VII-IX 中的比较表明,如果收敛速度很重要,L-SRTDE 能够胜过替代算法,包括在 10 D 10D 10D 情况下的 EBOwithCMAR。然而,Friedman 排序和 U-scores 显示,在 10 D 10D 10D 中第二好的算法是 EA4eigN100 或 LSHADE-SPACMA,在 30 D 30D 30D 中则是 L-SHADE-RSP。
图 2 和图 3 显示了所考虑算法在 30 D 30D 30D 情况下的收敛图。
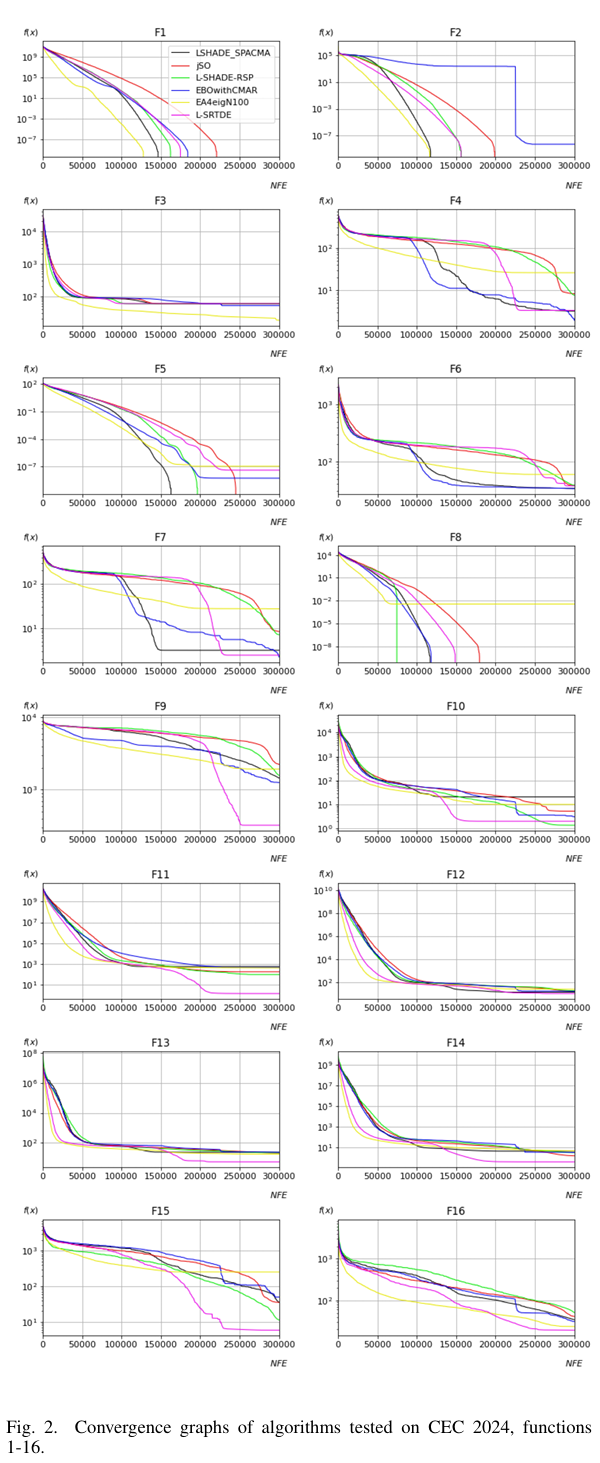
图 2.在 CEC 2024 上测试的算法的收敛图,函数 1-16。
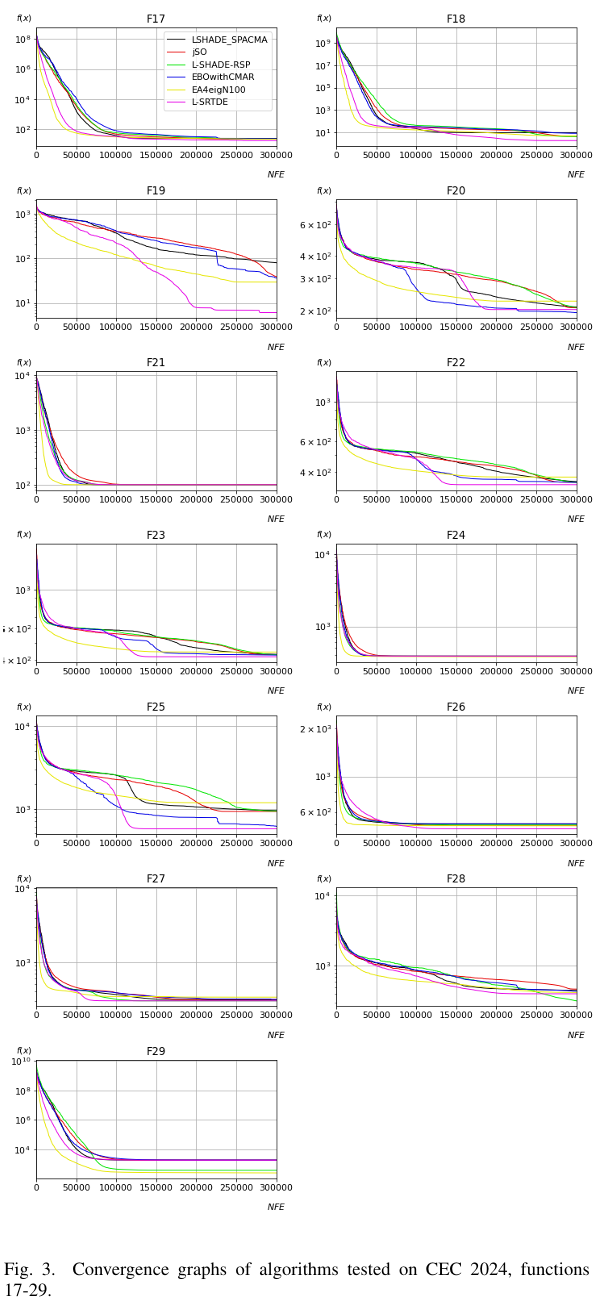
图 3.在 CEC 2024 上测试的算法的收敛图,函数 17-29。
从图 2 和 3 可以看出,在简单的单峰函数(如 F1 或 F2)上,L-SRTDE 并不总是比其他方法更快地达到最优解,但在多峰函数(如 F7, F9)以及混合函数(F11, F13, F14, F15, F18, F19)和复合函数(F22, F23, F26)上能够取得更好的结果。
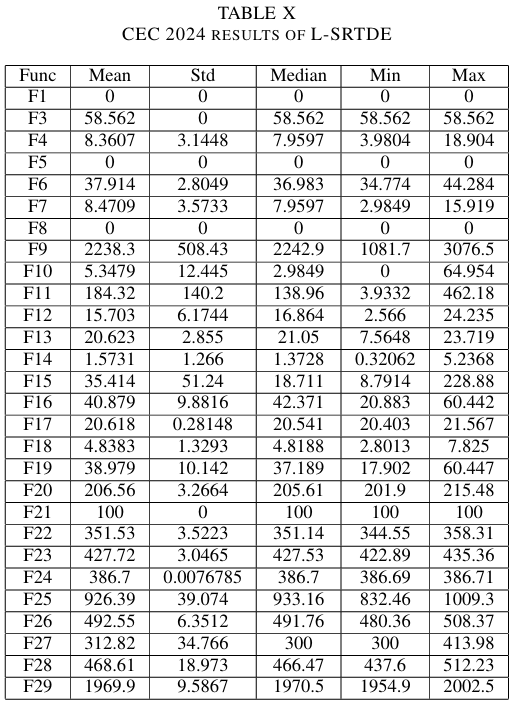
表 X 包含了 L-SRTDE 在 CEC 2024 所有 29 个函数上的平均值、中位数、最小值、最大值和标准差。
对于时间复杂度测量,计算了两个值。 T 1 T1 T1 是在 30 D D D 下评估 29 个函数中每个函数 10000 次的平均时间, T 2 T2 T2 是算法在允许 10000 次评估的情况下运行的平均时间。 T 1 T1 T1 值为 0.0644 0.0644 0.0644, T 2 T2 T2 为 0.0721 0.0721 0.0721,复杂度度量为 ( T 2 − T 1 ) / T 1 = 0.1195 (T2-T1)/T1=0.1195 (T2−T1)/T1=0.1195。
V 结论
本文提出了 L-SRTDE 算法,它与许多 DE 算法不同,因为它使用了两个种群、源自 L-NTADE 的特定变异和选择机制。L-SRTDE 的主要特点之一是基于成功率的缩放因子自适应,它遵循一个简单的依赖关系。在三个不同基准上的实验结果表明,这种参数值设置使得 L-SRTDE 在不同基准上使用相同参数集的情况下,能够表现出优于替代方法的性能。
参考文献
-
[1] K. Price, R. Storn, and J. Lampinen, Differential evolution: a practical approach to global optimization. Springer, 2005.
-
[2] S. Das, S. Muhtick, and P. Suganthan, “Recent advances in differential evolution - an updated survey,” Swarm and Evolutionary Computation, vol. 27, pp. 1-30, 2016.
-
[3] V. Stanovov, S. Akhmedova, and E. Semenkin, “Dual-population adaptive differential evolution algorithm l-ntade,” Mathematics, 2022.
-
[4] R. Tanabe and A. Fukunaga, “Success-history based parameter adaptation for differential evolution,” in Proceedings of the IEEE Congress on Evolutionary Computation. IEEE Press, 2013, pp. 71-78.
-
[5] V. Stanovov and E. Semenkin, “Genetic programming for automatic design of parameter adaptation in dual-population differential evolution,” Proceedings of the Companion Conference on Genetic and Evolutionary Computation, 2023. [在线]. 可用: https://api.semanticscholar.org/CorpusID:260119279
-
[6] ----, “Surrogate-assisted automatic parameter adaptation design for differential evolution,” Mathematics, vol. 11, no. 13, 2023. [在线]. 可用: https://www.mdpi.com/2227-7390/11/13/2937
-
[7] N. Awad, M. Ali, J. Liang, B. Qu, and P. Suganthan, “Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective bound constrained real-parameter numerical optimization,” Nanyang Technological University, Singapore, Tech. Rep., 2016.
-
[8] A. Kumar, K. Price, A. K. Mohamed, A. A., and P. N. Suganthan, “Problem definitions and evaluation criteria for the cec 2022 special session and competition on single objective bound constrained numerical optimization,” Nanyang Technological University, Singapore, Tech. Rep., 2021.
-
[9] K. Qiao, X. Wen, X. Ban, P. Chen, K. V. Price, P. N. Suganthan, J. Liang, G. Wu, and C. Yue, “Evaluation criteria for cec 2024 competition and special session on numerical optimization considering accuracy and speed,” Zhengzhou University, Central South University, Henan Institute of Technology, Qatar University, Tech. Rep., 2023.
-
[10] J. Zhang and A. C. Sanderson, “Jade: Self-adaptive differential evolution with fast and reliable convergence performance,” 2007 IEEE Congress on Evolutionary Computation, pp. 2251-2258, 2007.
-
[11] V. Stanovov, S. Akhmedova, and E. Semenkin, “Nl-shade-rsp algorithm with adaptive archive and selective pressure for cec 2021 numerical optimization,” in 2021 IEEE Congress on Evolutionary Computation (CEC), 2021, pp. 809-807.
-
[12] P. Kolenovsky and P. Bujok, “An adaptive variant of jso with multiple crossover strategies employing eigen transformation,” 2022 IEEE Congress on Evolutionary Computation (CEC), pp. 1-8, 2022. [在线]. 可用: https://api.semanticscholar.org/CorpusID:252112917
-
[13] R. Biedrzycki, J. Arabas, and D. Jagodzinski, “Bound constraints handling in differential evolution: An experimental study,” Swarm Evol. Comput., vol. 50, 2019.
-
[14] D. Zaharie, “Critical values for the control parameters of differential evolution algorithms,” Proc. of MENDEL 2002, 8th Int. Conf. on Soft Computing, vol. 2, pp. 62-67, 01 2002.
-
[15] A. Qin and P. Suganthan, “Self-adaptive differential evolution algorithm for numerical optimization,” in Proceedings of the IEEE Congress on Evolutionary Computation, 2005, pp. 1785-1791.
-
[16] J. Brest, S. Greiner, B. Boskovic, M. Memik, and V. Zumer, “Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 6, pp. 646-657, 2006.
-
[17] J. Brest, M. Maucec, and B. Bovskovic, “The 100-digit challenge: Algorithm jde100,” 2019 IEEE Congress on Evolutionary Computation (CEC), pp. 19-26, 2019.
-
[18] J. Brest, M. Maucec, and B. Boskovic, “Differential evolution algorithm for single objective bound-constrained optimization: Algorithm j2020,” 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1-8, 2020.
-
[19] V. Stanovov, S. Akhmedova, and E. Semenkin, “Biased parameter adaptation in differential evolution,” Information Sciences, vol. 566, pp. 215-238, 2021.
-
[20] R. Tanabe and A. Fukunaga, “Improving the search performance of SHADE using linear population size reduction,” in Proceedings of the IEEE Congress on Evolutionary Computation, CEC, Beijing, China, July 2014, pp. 1658-1665.
-
[21] W. Gong and Z. Cai, “Differential evolution with ranking-based mutation operators,” IEEE Transactions on Cybernetics, vol. 43, pp. 2066-2081, 2013. [在线]. 可用: https://api.semanticscholar.org/CorpusID:1755811
-
[22] V. Stanovov, S. Akhmedova, and E. Semenkin, “I-shade algorithm with rank-based selective pressure strategy for solving cec 2017 benchmark problems,” 2018 IEEE Congress on Evolutionary Computation (CEC), pp. 1-8, 2018.
-
[23] T. Kitamura and A. Fukunaga, “Differential evolution with an unbounded population,” 2022 IEEE Congress on Evolutionary Computation (CEC), 2022.
-
[24] E. Burke, M. Hyde, G. Kendall, G. Ochoa, E. Ozcan, and J. Woodward, A Classification of Hyper-Hewitt’s Approaches: Revisited. Springer International Publishing, 2019, pp. 453-477.
-
[25] V. Stanovov, L. Kazakovtsev, and E. Semenkin, “Hyper-heuristic approach for tuning parameter adaptation in differential evolution,” Axions, vol. 13, p. 59, 2024. [在线]. 可用: https://api.semanticscholar.org/CorpusID:267108274
-
[26] W. Gong, Z. Cai, and Y. Wang, “Repairing the crossover rate in adaptive differential evolution,” Appl. Soft Comput., vol. 15, pp. 149-168, 2014. [在线]. 可用: https://api.semanticscholar.org/CorpusID:41345493
-
[27] K. V. Price, A. Kumar, and P. N. Suganthan, “Trial-based dominance for comparing both the speed and accuracy of stochastic optimizers with standard non-parametric tests,” Swarm Evol. Comput., vol. 78, p. 101287, 2023.
-
[28] A. Mohamed, A. A. Hadi, A. Fattouh, and K. Jambi, “Lshade with semi-parameter adaptation hybrid with cma-es for solving cec 2017 benchmark problems,” 2017 IEEE Congress on Evolutionary Computation (CEC), pp. 145-152, 2017.
-
[29] J. Brest, M. Maucec, and B. Boskovic, “Single objective real-parameter optimization algorithm jSO,” in Proceedings of the IEEE Congress on Evolutionary Computation. IEEE Press, 2017, pp. 1311-1318.
-
[30] A. Kumar, R. K. Misra, and D. Singh, “Improving the local search capability of effective butterfly optimizer using covariance matrix adapted retreat phase,” 2017 IEEE Congress on Evolutionary Computation (CEC), pp. 1835-1842, 2017.
-
[31] V. Stanovov, S. Akhmedova, and E. Semenkin, “Ni-shade-lbc algorithm with linear parameter adaptation bias change for cec 2022 numerical optimization,” 2022 IEEE Congress on Evolutionary Computation (CEC), 2022.
-
[32] A. W. Mohamed, A. A. Hadi, P. Agrawal, K. M. Sallam, and A. K. Mohamed, “Gaining-sharing knowledge based algorithm with adaptive parameters hybrid with imode algorithm for solving cec 2021 benchmark problems,” 2021 IEEE Congress on Evolutionary Computation (CEC), pp. 841-848, 2021.
-
[33] L. V. Cuong, N. N. Bao, and H. T. T. Binh, “Technical report: A multi-start local search algorithm with l-shade for single objective bound constrained optimization,” SoICT, Hanoi University of Science and Technology, Vietnam, Tech. Rep., 2021.
-
[34] S. Biswas, D. Saha, S. De, A. D. Cobb, S. Das, and B. Jalaian, “Improving differential evolution through bayesian hyperparameter optimization,” 2021 IEEE Congress on Evolutionary Computation (CEC), pp. 832-840, 2021.
-
[35] P. Bujok and P. Kolenovsky, “Eigen crossover in cooperative model of evolutionary algorithms applied to cec 2022 single objective numerical optimisation,” 2022 IEEE Congress on Evolutionary Computation (CEC), 2022.
-
[36] R. Biedrzycki, J. Arabas, and E. Warchulski, “A version of nl-shade-rsp algorithm with midpoint for cec 2022 single objective bound constrained problems,” 2022 IEEE Congress on Evolutionary Computation (CEC), 2022.
