当前位置：首页 > news >正文

十字链表的构建和操作

news 2025/10/15 14:44:27

前面两期给大家讲解了两种关于构建图的算法，分别是邻接矩阵和邻接表，但这两种算法分别都有各自的缺陷，比如说邻接矩阵的空间复杂度太大，邻接表寻找有向图的入度极其困难，今天给大家介绍一中存储有向图比邻接表更加优秀的算法-----十字链表法

邻接表的缺陷无非就是寻找入度的时候时间复杂度较大，我们可以在创建结构体的时候在里面入度的成员，这样访问的时候就会非常便捷。

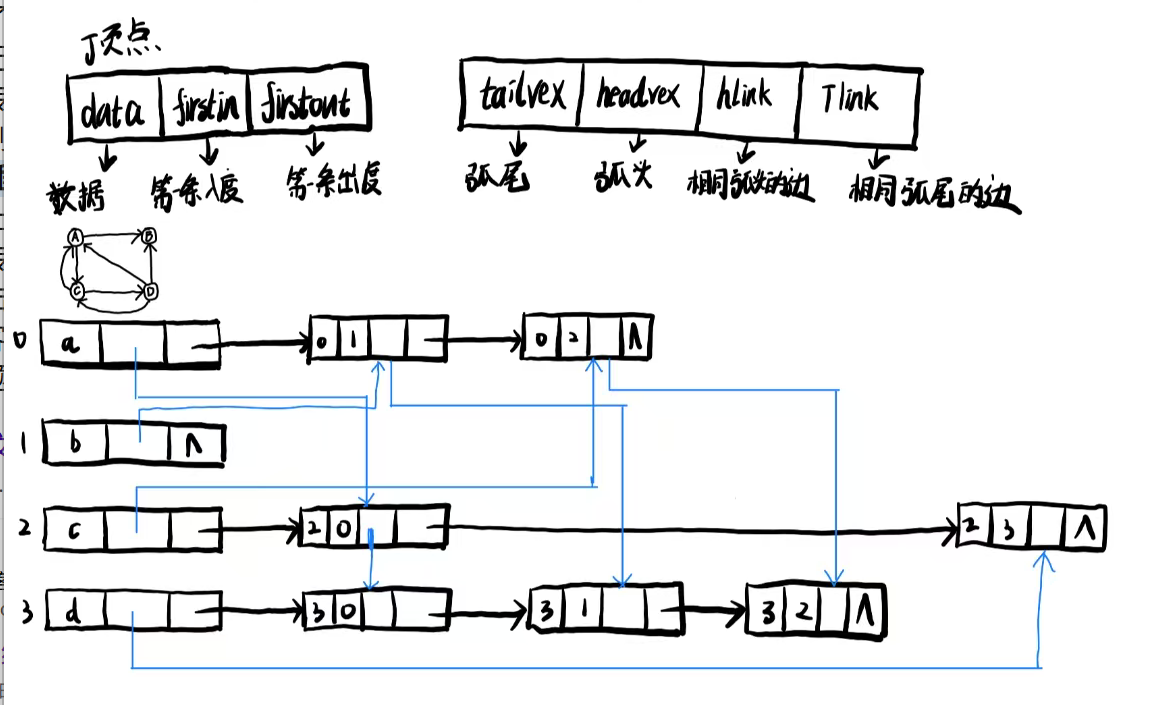
这个图里面分别有两个结构体

第一个是顶点的，里面存储了数组域和第一条入度和第一条出度，这样我们在寻找的时候只需要找到第一个然后依次寻找即可

第二个是边的结构体，里面存储是数组元素的下标其实就是弧头和弧尾指向的顶点，另外两个是下一个弧头和下一个弧尾

具体代码:

//十字链表法
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#define MAX 4//假设有四个元素
//边的结构体
typedef struct Edge
{
   int tailvex, headvex;//弧头和弧尾编号
   struct Edge* HLinkNext;//相同弧头的下一条弧
   struct Edge* TLinkNext;//相同弧尾的下一条弧
}Edge;
//顶点结构体
typedef struct Vertex
{
   char data;//数据域
   struct Edge* firstin, * firstout;//第一条入度弧和第一条出度弧
}Vertex;
//定义图
typedef struct Graph
{
   Vertex arr[MAX];//数组元素的数组
   int num;//顶点数量
}Graph;
//初始化
void InitGraph(Graph * G)
{
   G->num = 0;
   int i;
   for (i = 0; i < MAX; i++)
   {
       //还未添加顶点
       G->arr[i].data = '\0';
       G->arr[i].firstin = NULL;
       G->arr[i].firstout = NULL;
   }
   return;
}
//添加顶点
bool EnGraph(Graph* G)
{
   if (G->num > MAX)
       return false;//元素个数大于数组长度
   int i;
   for (i = 0; i < MAX; i++)
       G->arr[i].data = 'A' + i;//给数组赋值
   G->num = MAX;
   return true;
}
//添加边
bool EnEdge(Graph* G,int from,int to)
{
   if (G->num > 4 || G->num < 0)
       return false;//数据不合法
   //创建A -> B
   Edge* e = (Edge*)malloc(sizeof(Edge));
   if (e == NULL)
       return false;//分配空间失败
   //赋值
   e->headvex = from;
   e->tailvex = to;
   //为顶点建立连接
   //建立出度连接(头插法)
   e->TLinkNext = G->arr[from].firstout;
   G->arr[from].firstout = e;
   //建立入度连接(头插法)
   e->HLinkNext = G->arr[to].firstin;
   G->arr[to].firstin = e;
   return true;
}
//查到顶点的出度和入度
bool FindDegree(Graph * G,char ch)
{
   if (G->num == 0)
       return false;//非图
   int index = -1;
   //查找ch是否存在
   for (int i = 0; i < MAX; i++)
   {
       if (G->arr[i].data == ch)
       {
           index = i;
           break;
       }
   }
   if (index == -1)
       return false;//不存在该顶点
   Edge * DegreeIn = G->arr[index].firstin;
   Edge* DegreeOut = G->arr[index].firstout;
   //求入度
   while (DegreeIn != NULL)
   {
       printf("%c的入度为%c\n", ch, G->arr[DegreeIn->headvex].data);
       DegreeIn = DegreeIn->HLinkNext;
   }
   //求出度
   while (DegreeOut != NULL)
   {
       printf("%c的出度为%c\n", ch, G->arr[DegreeOut->tailvex].data);
       DegreeOut = DegreeOut->TLinkNext;
   }

   return true;
}
int main()
{

   Graph G;//定义图
   InitGraph(&G);//初始化图
   EnGraph(&G);//添加顶点
   //添加边
   //A->B A->C
   EnEdge(&G, 0, 1);
   EnEdge(&G, 0, 2);
   //C->A C->D
   EnEdge(&G, 2, 0);
   EnEdge(&G, 2, 3);
   //D->A D->B D->C
   EnEdge(&G, 3, 0);
   EnEdge(&G, 3, 1);
   EnEdge(&G, 3, 2);