当前位置：首页 > news >正文

【Datawhale组队学习】math-for-ai TASK01

news 2025/10/15 14:28:58

机器学习：设计算法，自动从数据中提取有价值的信息
机器学习关注的是可应用于许多数据集的通用方法，同时产生有意义的东西。

三个核心概念：数据、概念和学习

机器学习本质上是数据驱动的。数据是机器学习的核心。
机器学习的目标是设计通用方法，从数据中提取有价值的模式，理想情况下无需太多特定领域的专业知识。
如果一个模型在考虑的了数据之后，在给定任务上的表现有所改善，那么这个模型就可以说是从数据中学习的
我们的目标是找到能很好地泛化到我们将来可能会关注的未见数据的好模型。学习可以理解为一种通过优化模型参数来自动发现数据中的模式和结构的学习方法。

为直觉寻找词语

机器学习系统的某个特定组件可以抽象为不同的数学概念。例如，在机器学习中，“算法 ”一词至少有两种不同的含义。
第一种意义：使用机器学习算法来根据输入数据进行预测的系统。我们将这些算法称为预测器。
第二种意义：我们使用完全相同的短语“机器学习算法”来指一种系统，它可以调整预测器的某些内部参数。从而使其在未来未见到的数据表现良好。在这里，我们将这种调整称为训练系统。
要理解“机器学习算法”两种含义的核心差异，关键不在于“是否做预测”，而在于系统的核心目标、角色定位和运行阶段完全不同——一个是“执行预测的工具”，一个是“优化工具的工具”。二者的差异具体体现在以下5个核心维度，我们可以通过对比和实例更清晰地理解：

对比维度	第一种含义：预测器（Predictor）	第二种含义：训练系统（Training System）
核心目标	接收新输入→输出预测结果（“用工具干活”）	接收数据→调整预测器参数→让预测器更准（“打磨工具”）
角色定位	「最终执行预测的成品」（如训练好的模型）	「生产/优化成品的机器」（如训练流程本身）
运行依赖	依赖“已固定的内部参数”（参数是训练好的，不会再变）	依赖“原始数据+待优化的预测器”（参数是动态调整的）
作用阶段	机器学习的「推理阶段」（Inference Phase）——模型用起来的时候	机器学习的「训练阶段」（Training Phase）——模型造出来的时候
用户直接接触度	高（用户用它做预测，如“用模型判断邮件是否是垃圾邮件”）	低（通常是算法工程师用它调模型，用户感知不到）

在本书中，我们假定数据已经被适当地转换成适合读入计算机程序的数字表示形式。因此，我们将数据视为向量。
向量是数据的另一种表现形式，它说明了文字是多么微妙，我们可以（至少）用三种不同的方式来思考向量：

向量是一个数字数组（计算机科学观点）、
向量是一个有方向和大小的箭头（物理学观点）
向量是一个服从加法和缩放的对象（数学观点）。

模型通常用于描述生成数据的过程，与手头的数据集类似。因此，好的模型也可以被看作是真实（未知）数据生成过程的简化版本，捕捉对建模数据并提取隐藏模式中至关重要的特征。好的模型可以用来预测真实世界中会发生的事情，而无需进行真实世界的实验。

机器学习的学习部分
假设我们得到了一个数据集和一个合适的模型。
训练模型意味着利用现有数据优化模型的某些参数，而模型的参数与效用函数相关，效用函数用于评估模型对训练数据的预测效果。
大多数训练方法可以看作是一种类似于爬山到达山顶的方法。在这种类比中，山顶对应的是某种所需的性能指标的最大值。然而，在实践中，我们希望模型在未见过的数据上表现良好。在我们已经见过的数据（训练数据）上表现良好，可能只意味着我们找到了记忆数据的好方法。然而，这可能并不能很好地推广到未见过的数据上，而且在实际应用中，我们经常需要让机器学习系统面对它以前从未遇到过的情况。

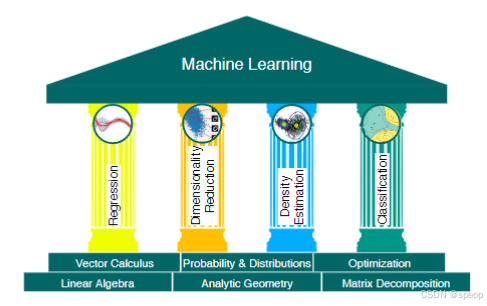
在这里插入图片描述
机器学习基础的四大支柱：

回归

向量微积分
线性代数

降维

概率与分布
解析几何

密度估计
分类

优化
矩阵分解

关于数学

向量来表示数值数据，用矩阵来表示这些数据的表格
对向量和矩阵的研究称为线性代数
线性代数章节介绍了将向量集合为矩阵的方法

给定现实世界中两个物体的向量，要对它们的相似性做出说明
我们的机器学习算法（我们的预测器）应该预测相似的向量会有相似的输出。为了使向量间的相似性概念正规化，我们需要引入一些操作，将两个向量作为输入，并返回一个代表其相似性的数值。相似性和距离的构造是解析几何的核心

我们通常认为数据是对某些真实潜在信号的噪声观测。
我们希望通过应用机器学习，从噪声中识别出信号。这就要求我们有一种语言来量化 “噪声 ”的含义。我们通常还希望预测器能让我们表达某种不确定性，例如，量化我们对特定测试数据点的预测值的信心。不确定性的量化属于概率论的范畴，将在第 6 章中介绍。

关于机器学习

在第8章中，我们以数学的方式重述了机器学习的三个组成部分（数据、模型和参数估计）。此外，我们就如何设计机器学习实验评估方案提供了若干指导原则，以防止对机器学习系统的评估过于乐观。回顾一下，我们的目标是建立一个在未见数据上表现良好的预测器

在第9章中，我们将仔细研究线性回归，我们的目标是找到将输入 $x∈RDx∈\mathbb{R}^D$ 映射到或对应的观测函数值 $y∈Ry\in \mathbb{R}$ 的函数，我们可以将其解释为各自输入的标签。我们将讨论通过最大似然估计和最大后验估计进行的经典模型拟合(参数估计)，以及贝叶斯线性回归，在贝叶斯线性回归中，我们对参数进行积分而不是优化。

最大似然估计 让数据最可能出现的参数。
- 找到一个参数值 θ，使得 “在这个参数下，我们观测到当前这批数据的概率最大”。简单说：数据已经发生了，哪个参数 θ 最能 “解释” 这个数据的出现？θ 就是最优估计。
最大后验估计 结合先验知识后，数据最可能出现的参数。
除了数据本身，还引入对参数 $θ\theta$ 的先验知识。（比如 “硬币大概率是公平的，θ 更可能在 0.5 附近”），然后找到 “在已有数据和先验知识共同作用下，最可能的参数 θ”。
简单说：不仅看数据怎么说，还看 “常识” 怎么说，综合两者后选一个最合理的参数。
后验估计中的先验知识未必是从数据中获取的，可以是直觉性常识，也可以来自其他多种渠道，

第 10 章的重点是利用主成分分析法降维，即图 1.1 中的第二个支柱。降维的主要目的是为高维数据 $x∈RDx∈\mathbb{R}^D$ 找到一个紧凑的低维表示，它通常比原始数据更容易分析。与回归不同的是，降维只关注数据建模–数据点x没有相关标签。
本质是说：大多数降维方法（如 PCA、t-SNE）是 “无监督” 的 —— 它们只盯着 “数据点自身的特征分布”（比如哪些数据点近、哪些远、整体方差在哪）做维度压缩，完全不管数据点有没有被标注 “类别”“目标值” 这些额外标签，也不根据标签调整降维方向

无监督降维（大多数基础降维方法）：如 PCA、t-SNE、UMAP、KPCA，对应这句话的描述 —— 只关注数据点，无标签。它们的优势是 “不依赖标注成本”（现实中很多数据没有标签），能从原始数据中自动挖掘结构；
有监督降维（少数特殊降维方法）：如 LDA（线性判别分析）、LLE 的有监督变体，依赖标签。它们的目标是 “降维后的数据能更好地服务于标签相关任务”（比如 LDA 会让 “同一标签的数据点更集中，不同标签的数据点更分离”），但这种方法需要先有标签，不属于这句话描述的 “只关注数据点” 的范畴。

第11章
我们将转向第三个支柱：密度估计。密度估计的目标是找到描述给定数据集的概率分布。为此，我们将重点关注高斯混合模型，并讨论一种迭代方案来找到该模型的参数。与降维一样，数据点 $x∈RDx\in \mathbb{R}^D$ 没有相关标签。然而，我们并不寻求数据的低维表示。相反，我们感兴趣的是能描述数据的密度模型。
高斯分布是现实中数据最常呈现的分布形态：数据会围绕一个 “中心点”（均值）集中，越靠近中心点的数据越多，越远离的数据越少，整体呈 “钟形曲线”。