当前位置：首页 > news >正文

LeetCode算法日记 - Day 72: 下降路径最小和、珠宝的最高价值

news 2025/10/15 14:26:14

1. 下降路经最小和

1.1 题目解析

1.2 解法

1.3 代码实现

2. 珠宝的最高价值

2.1 题目解析

2.2 解法

2.3 代码实现

1. 下降路经最小和

https://leetcode.cn/problems/minimum-falling-path-sum/description/

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

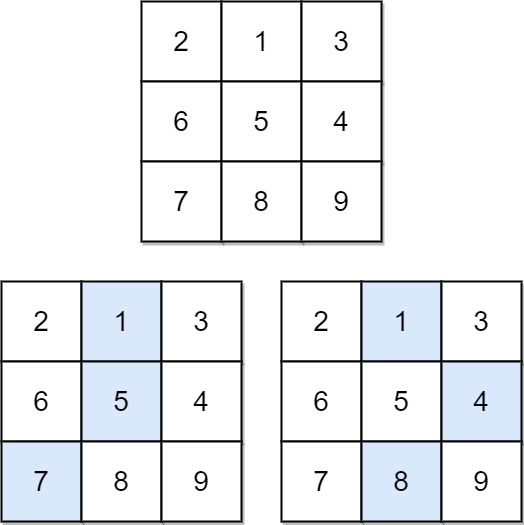
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

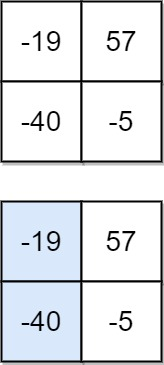
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

1.1 题目解析

题目本质
这是一个「路径代价最优化」问题，需要在一个二维矩阵中，从第一行的任意位置出发，每次只能向下移动到相邻的三个位置之一，找到到达最后一行的最小路径和。

常规解法
递归枚举所有可能的路径，对每个位置尝试三个方向（左下、正下、右下），计算所有路径的和，取最小值。

问题分析
暴力递归会导致大量重复计算。比如到达 (2,1) 这个位置可能有多条路径，但每次都要重新计算从这里到底部的最小代价。对于 n×n 的矩阵，时间复杂度是指数级 O(3^n)，完全无法接受。

思路转折
"
这种「无后效性」特征提示我们可以用动态规划：从上往下逐行计算，每个位置只需要知道上一行的结果即可，避免重复计算。预处理所有位置的最小路径和后，最后一行的最小值就是答案。

1.2 解法

算法思想

使用动态规划，定义 dp[i][j] 表示从第一行出发，到达位置 (i,j) 的最小路径和。

递推关键：正向思考是"当前位置能去下面三个格子"，反向递推就是"当前格子的最优解来自上面三个相邻格子之一"

dp[i][j] = matrix[i][j] + min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1])

注意边界处理：左右边界的位置只有两个上方来源。

i）初始化 dp 数组（可以用 1-索引或 0-索引）

ii）第一行直接赋值为 matrix 的第一行

iii）从第二行开始，逐行计算每个位置的最小路径和：

从正上方 dp[i-1][j] 转移

从左上方 dp[i-1][j-1] 转移（j>0 时）

从右上方 dp[i-1][j+1] 转移（j<n-1 时）

取三者最小值加上当前位置的值

iv）遍历最后一行，找出最小值

易错点

索引映射混淆：如果 dp 用 1 开始当索引（大小 [m+1][n+1]），访问 matrix 时必须是 matrix[i-1][j-1]，不能直接用 matrix[i][j]，否则会越界

需要遍历完整的 n 列，循环应该是 j <= n 而不是 j < n
初始化问题：第一行需要特殊处理，或者确保 dp 数组第 0 行初始化为 0

1.3 代码实现

class Solution {int[][] dp;public int minFallingPathSum(int[][] matrix) {int m = matrix.length, n = matrix[0].length;dp = new int[m+1][n+1];for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){int cur = dp[i-1][j];  // 正上方if(j > 1)  cur = Math.min(cur, dp[i-1][j-1]);  // 左上方if(j < n)  cur = Math.min(cur, dp[i-1][j+1]);  // 右上方dp[i][j] = matrix[i-1][j-1] + cur;  // 注意索引映射}}int ret = Integer.MAX_VALUE;for(int j = 1; j <= n; j++){  // 遍历最后一行的所有列ret = Math.min(ret, dp[m][j]);}return ret;}
}

复杂度分析

时间复杂度：O(n²)，需要遍历整个 n×n 矩阵，每个位置计算常数次比较。

空间复杂度：O(n²)，使用了 dp 数组存储所有位置的结果。可以优化到 O(n)，只保留上一行的数据即可。

2. 珠宝的最高价值

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

示例 1：

输入：frame = [[1,3,1],[1,5,1],[4,2,1]]
输出：12
解释：路径 1→3→5→2→1 可以拿到最高价值的珠宝

提示：

0 < frame.length <= 200
0 < frame[0].length <= 200

2.1 题目解析

题目本质
这是一个「网格路径最优化」问题，在二维矩阵中从固定起点（左上角）到固定终点（右下角），每次只能向右或向下移动，求路径上数字和的最大值。

常规解法
递归枚举所有可能的路径，对每个位置尝试向右或向下两个方向，计算所有从起点到终点的路径和，取最大值。

问题分析
暴力递归会产生大量重复计算。从 (0,0) 到 (i,j) 可能有多条路径，但每次都要重新计算这段路径的最大值。对于 m×n 的矩阵，可能的路径数是组合数 C(m+n-2, m-1)，规模较大时完全不可行。

思路转折
观察到每个位置的最优解只依赖于它的上方和左方位置——因为只能从这两个方向过来。这种局部最优可以推导全局最优的特性，提示我们用动态规划
从左上角开始逐行或逐列计算，每个位置取"从上来"和"从左来"的较大值，最终右下角就是答案。这样每个格子只计算一次，大幅降低复杂度。

2.2 解法

算法思想

使用动态规划，定义 dp[i][j] 表示从起点 (0,0) 走到位置 (i,j) 能获得的最大珠宝价值。

递推公式：

dp[i][j] = frame[i][j] + max(dp[i-1][j], dp[i][j-1])

递推关键：正向思考是"当前位置能去右边或下边"，反向递推就是"当前位置的最优解来自上方或左方的较大者"。

i）初始化 dp 数组（可以用 [m+1][n+1] 的 1-索引，或 [m][n] 的 0-索引）

ii）从 (1,1) 开始（或 (0,0)），逐行或逐列遍历每个位置

iii）对每个位置 (i,j)：

从上方转移：dp[i-1][j]

从左方转移：dp[i][j-1]

取两者最大值，加上当前位置的珠宝价值

iv）返回 dp[m][n]（右下角的值）

易错点

索引映射：如果 dp 用 1-索引（大小 [m+1][n+1]），访问 frame 时要用 frame[i-1][j-1]，不然会越界

边界初始化：使用 [m+1][n+1] 大小的好处是自动处理边界——第 0 行和第 0 列都是 0，不需要特殊处理第一行第一列

返回值位置：最终答案在 dp[m][n]，不是 dp[m-1][n-1]（如果用 1-索引）

移动方向限制：只能向右或向下，不能向左向上，所以递推时只需要考虑上方和左方两个来源

2.3 代码实现

class Solution {int[][] dp;public int jewelleryValue(int[][] frame) {int m = frame.length, n = frame[0].length;dp = new int[m+1][n+1];  // 1-索引，自动处理边界for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){// 当前价值 = 当前珠宝 + max(从上来, 从左来)dp[i][j] = frame[i-1][j-1] + Math.max(dp[i-1][j], dp[i][j-1]);}}return dp[m][n];  // 右下角就是答案}
}

复杂度分析