波矢 行波 和 相速度推导

波矢

对于弦波，我们知道要描述他在时间上的周期性，常用 角频率 $$\omega =\frac{2\pi }{T}$$ 。 那如果要描述空间上的周期性呢？ 那就要引入波矢了。

我们定义波矢的数量是：$$|\vec{k}|=\frac{2\pi }{\lambda }其中\lambda 是波长$$， 而波矢作为一个矢量，他的方向是波的传播方向。这个在某些学科里，也叫做波数。可见，波长越短，波矢越大，说明单位空间内容纳的波个数越多。这和角频率有异曲同工之妙。

如果我们已经知道了波的波矢为|k| ,

• 请问1m中有多少个波周期？
• 请问一维波，在xm 中，有多少个波周期？
• 某点真正重要的是“相位”， 在xm 处，相比0m 处，相位差如何？

$$\begin{gathered} 对于y=Acos(x),他的距离周期是2pi(m), \\ 对于y=Acos(kx)，他的距离周期是2pi/k(m) \\ (可以想到，k=2时候，x=pi就完成一个周期) \\ 所以，距离频率f_x=1/X=\frac{k}{2\ast \pi }(1/m) \\ 所以，1m中有fx\ast 1m=k/(2pi)=1/\lambda 个波 \\ ---------------------------------------- \\ 那xm,等倍扩大即可有\frac{x}{\lambda } \\ ---------------------------------------- \\ 一个周期对应2\pi ,那xm处相比0m处相位增长了\frac{2\pi x}{\lambda } \\ 也就是kx从上面的推导，我们可以得出|k|波矢的数学意义就是：1m的距离带来的相位变化量。 \\ \boxed{\Delta {\varphi }_x=|k|x}(一维情况) \\ \boxed{\Delta {\varphi }_{\vec{r}}=\vec{k}\vec{x}}(高维情况) \end{gathered}$$

行波方程

下面讲讲一般的一维行波（最常见的传递形式）的数学表达:
$$\begin{gathered} \Phi (x,t)=Acos(kx-\omega t+\varphi ) \\ (\varphi 是初始相位，定值) \end{gathered}$$
下面我们讲讲怎么理解这个式子:
$$\begin{gathered} 对于行波，其实最重要的就是某点的相位，时间和空间只是通过影响相位来影响某点波的强度的。 \\ 波矢和角速度意义是相同的，都是某一个度量对于相位影响的比例系数 \end{gathered}$$
所以这个式子可以这么写：
$$\begin{gathered} 记：\theta (x,t)=kx-\omega t+\varphi \\ \Phi (x,t)=Acos(\theta (x,t)) \end{gathered}$$
这个转化非常重要，这样就把一个复杂的弦函数转化成了一个熟悉的比例函数，我们只需要研究这个相位函数的值就行了。

在这里，你也许还不明白X 和T 是如何影响相位的，进而影响振幅的高低。

嗯，沉溺于数学推导只会让人变得繁杂琐碎。让我们先丢掉那些该死的符号，先想想一个最简单的场景：你是如何察觉到行波的运动的？

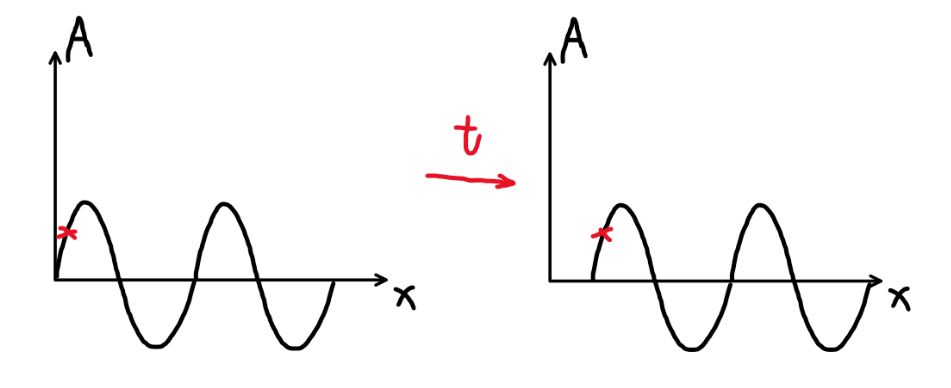
上面的是示意图，左侧是时刻1 在经过t 后， 变成了右侧。我们可以很直观的察觉：行波在向右运动。那具体来说，我们其实是找准了一个点，找到他后一个时刻高度相同的点（本质是相位相同）。（但是不得不指出，这其实只是我们的“感觉”，因为点只在垂直于传播方向做上下运动）

那我们怎么把这种察觉，转变为公式呢？很简单，你的位置 x和时间 t都在变化，但你“感受”到的相位 θ却始终是 0，没有变化。那相位不随时间空间变化，那就是全导数是0啊！(骗你的，不可能不用高等数学理解这些东西ヾ(•ω•`)o）
$$\begin{gathered} d\theta =0 \\ 根据全微分公式：d\theta =\frac{\partial \theta }{\partial x}dx+\frac{\partial \theta }{\partial t}dt=0 \\ 容易求导：d\theta =\frac{\partial \theta }{\partial x}dx+\frac{\partial \theta }{\partial t}dt=kdx-\omega dt=0 \\ 整理：\frac{dx}{dt}=\frac{\omega }{k} \\ 这个就是相速度公式：\boxed{v_p=\frac{\omega }{k}} \\ （注意符号，但是这个公式非常容易推导，所以不建议死记公式） \\ (还有一点，这个相速度是dx/dt,相当于XT导数，所以正方向是X正) \end{gathered}$$
如果从立体几何角度来看呢？θ 其实和X T 构成了一个平面，而相位不变，就是一个垂直于θ的平面。这个平面的位置可以随意变化，但是截面上，必然有一条XT交线，这个交线的斜率不随平面位置变化而变化。这个斜率就是相速度。matlab 验证一下，代码就不写了。截个图得了。

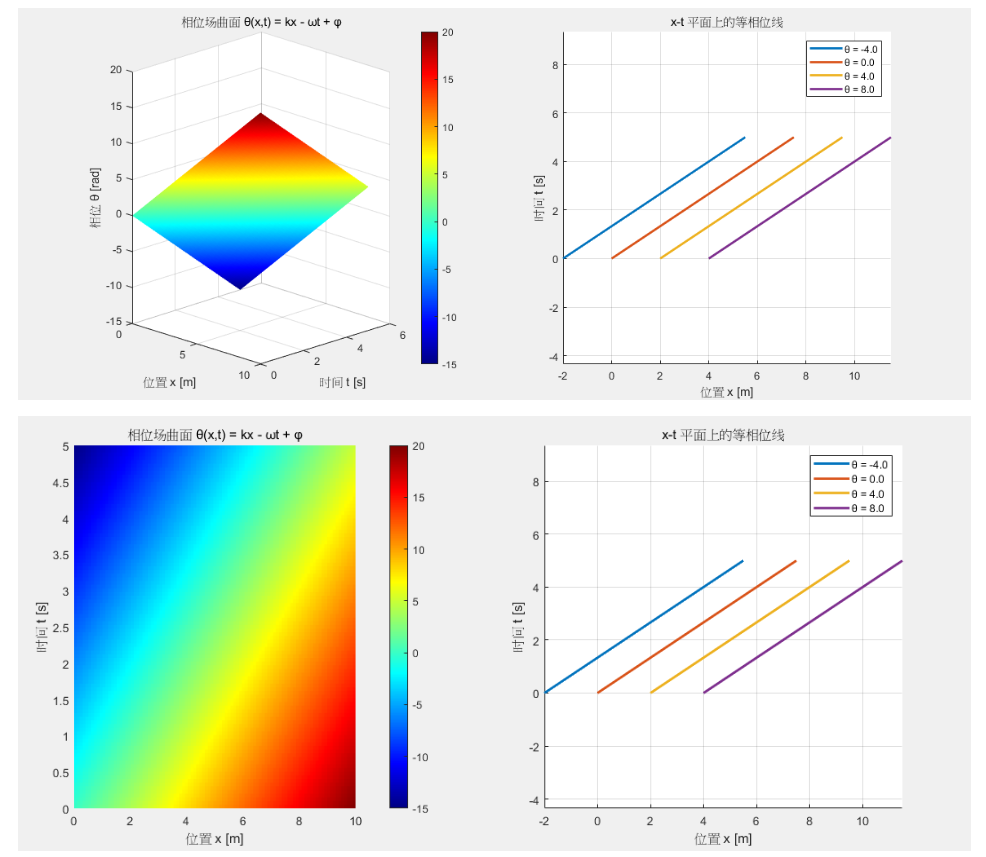
那我们来从这个图看看，这个波是怎么传播的？向左还是向右？

我们可以看出，同一个时间下，相位随着距离变大，同一个位置上，随着时间变小。那K和Ω都是大于零的，所以相速度大于零，而相速度是X关于T的导数，所以波朝着X正方向前进。

嗯，这里是在复习模拟集成电路，复习到器件，然后复习到半导体物理，最后发现量子物理有大坑的基本操作啊。我发现有些基础内容没搞懂，不过大四非常闲暇，所以直接刨根究底了。这次是在研究行波这个基础概念。