数据结构入门 (八):寻访节点的“路线图” —— 二叉树的深度与广度遍历
目录
- 引言:如何走遍一个“家族”
- 一、深度优先遍历 (DFS):递归的艺术
- 1.先序遍历 (Pre-order)
- 2.中序遍历 (In-order)
- 3.后序遍历 (Post-order)
- 二、广度优先遍历 (BFS):层层推进的涟漪
- 三、遍历的C语言实现
- 1.结构体与核心接口
- 2.创建二叉树和树节点
- 3.为指定父节点插入左右子节点
- 4.访问树节点(辅助函数)
- 5.递归实现的深度优先遍历
- 6.基于队列的广度优先遍历
- 7.测试函数
- 四、挑战极限:非递归的深度遍历
- 1.非递归先序遍历
- 2. 非递归中序遍历
- 3.栈的内容
- 4.测试函数
- 五、总结:探索的蓝图
引言:如何走遍一个“家族”
在上一篇文章中,我们绘制了“树”的静态蓝图。我们知道它是一个拥有根、分支和叶的层级“家族”。但是,一个静止的结构是没有生命力的。数据结构的真正威力,在于我们如何去操作它。
对于树而言,最基本、最重要的操作就是遍历——即按照某种特定的搜索路径,不重不漏地访问到家族中的每一个成员,且只访问一次。
对线性结构而言,遍历路线是唯一的。但对于树这种“开枝散叶”的结构,由于每个节点有多个后继,探访路线就有了丰富的选择。这就像玩游戏探索地图一样,在面对分叉路口时,有的人会选择先沿着一条路走到尽头再换路(深度优先),也有人会先把离入口最近的一圈先探索完再向外拓展(广度优先)。

这两种截然不同的“探访”策略,催生了二叉树最核心的遍历算法。
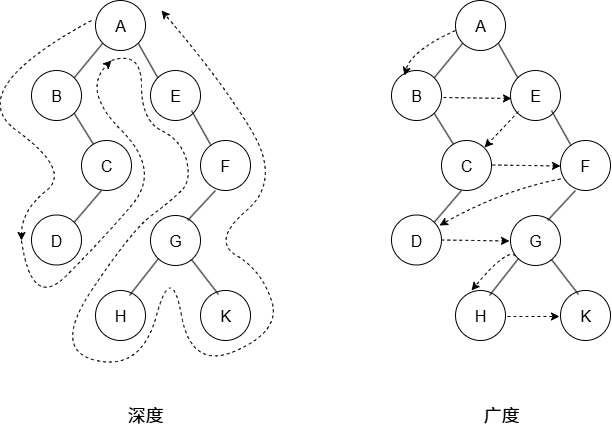
广度搜索也叫层次遍历,访问一个节点时(消费者),发现两个新任务(生产者)。引入队列缓存来解决。
一、深度优先遍历 (DFS):递归的艺术
深度优先,顾名思义,就是“不撞南墙不回头”。它选择一条分支,尽可能深地走下去,直到无路可走,才回溯到上一个路口,选择另一条分支继续探索。这种“走到底再回来”的行为模式,与递归的思想天然契合。
在探访任意一个节点(我们称之为“根”)及其左右子树时,我们实际上有三次机会来“处理”这个根节点本身:
- 刚踏入这片区域时(访问子树前)。
- 探访完左边分支回来后(访问右子树前)。
- 探访完所有分支,准备离开时(访问子树后)。
你选择在哪一个时机“处理”根节点,就决定了三种不同的深度优先遍历方式。
1.先序遍历 (Pre-order)
**规则:根 -> 左 -> 右
先处理当前节点,然后再依次递归探访其左、右子树。
遍历结果:ABCDEFGHK
2.中序遍历 (In-order)
规则:左 -> 根 -> 右
先递归探访左子树,待左子树全部结束后,再回来处理当前节点,最后再去探访右子树。
遍历结果:BDCAEHGKF
特别注意:对于一种特殊的二叉树——二叉搜索树,中序遍历可以得到一个有序的序列!
3.后序遍历 (Post-order)
规则:左 -> 右 -> 根
先递归探访完左、右所有子树,待所有“下属”都汇报完毕后,最后才处理当前节点。这种特性使其非常适合进行自底向上的计算,如计算目录大小或释放树节点内存。
遍历结果:DCBHKGFEA
二、广度优先遍历 (BFS):层层推进的涟漪
广度优先遍历,也叫层次遍历,它的探访方式与深度优先截然不同。它就像一颗石子投入水中,涟漪从中心开始,一圈一圈、一层一层地向外扩散。
这种“先处理完同辈,再处理下一代”的思想,是一个典型的生产者-消费者模型:
- 访问当前节点(消费者)。
- 该节点的左右孩子被视为新的待办任务(生产者)。
- 我们需要一个“等候区”来存放这些新任务,并保证先来的任务先被处理。
这个完美的“等候区”,就是我们早已熟知的数据结构——队列。
遍历步骤:
- 将根节点入队。
- 当队列不为空时,循环执行:
a. 出队一个节点,并访问它。
b. 如果该节点有左孩子,则左孩子入队。
c. 如果该节点有右孩子,则右孩子入队。
三、遍历的C语言实现
1.结构体与核心接口
#include <stdio.h>
#include <stdlib.h>typedef int Element;// 树的节点结构
typedef struct _tree_node
{Element data;struct _tree_node *left;struct _tree_node *right;
} TreeNode;// 二叉树的树头
typedef struct
{TreeNode *root;int count;
} BinaryTree;BinaryTree *createBinaryTree(TreeNode *root); // 创建一个新的二叉树对象
void releaseBinaryTree(BinaryTree *tree); // 释放整个二叉树及其所有节点占用的内存TreeNode *createTreeNode(Element e); // 创建一个单独的树节点void insertBinaryTree(BinaryTree *tree, TreeNode *parent, TreeNode *left, TreeNode *right); // 向二叉树中插入子节点
void visitTreeNode(const TreeNode *node); // 访问(打印或处理)一个树节点的数据void preOrderBTree(const BinaryTree *tree); // 先序遍历二叉树(递归版本)
void inOrderBTree(const BinaryTree *tree); // 中序遍历二叉树(递归版本)
void postOrderBTree(const BinaryTree *tree); // 先序遍历二叉树(递归版本)
void levelOrderBTree(const BinaryTree *tree); // 层序遍历二叉树(广度优先遍历)void preOrderBtreeNoRecursion(const BinaryTree *tree); // 先序遍历二叉树(非递归版本)
void inOrderBtreeNoRecursion(const BinaryTree *tree); // 先序遍历二叉树(非递归版本)
2.创建二叉树和树节点
BinaryTree* createBinaryTree(TreeNode* root) {BinaryTree *tree = malloc(sizeof(BinaryTree));if (tree == NULL) {fprintf(stderr, "tree malloc failed!\n");return NULL;}if (root) {tree->root = root;tree->count = 1;} else {tree->root = NULL;tree->count = 0;}return tree;
}TreeNode* createTreeNode(Element e) {TreeNode *node = malloc(sizeof(TreeNode));node->data = e; // 一个树节点包括数据和左右子树node->left = node->right = NULL;return node;
}
3.为指定父节点插入左右子节点
void insertBinaryTree(BinaryTree* tree, TreeNode* parent, TreeNode* left, TreeNode* right) {// 首先检查树和父节点指针是否有效,避免空指针解引用if (tree && parent) { // 建立链接:将父节点的左、右子指针分别指向传入的 left 和 right 节点parent->left = left;parent->right = right;// 只有当子节点存在(非 NULL)时,才将树的计数器加一if (left) {tree->count++;}if (right) {tree->count++;}}
}
4.访问树节点(辅助函数)
void visitTreeNode(const TreeNode* node)
{if (node)printf("\t%c", node->data); // 打印一个制表符,再打印节点数据
}
5.递归实现的深度优先遍历
递归的实现代码优雅而简洁,完美体现了DFS的思想。
// --- 先序遍历 ---
static void preOrderNode(const TreeNode *node) {if (node) {visitTreeNode(node); // 根preOrderNode(node->left); // 左preOrderNode(node->right); // 右}
}
void preOrderBTree(const BinaryTree* tree) {preOrderNode(tree->root);printf("\n");
}// --- 中序遍历 ---
static void inOrderNode(const TreeNode *node) {if (node) {inOrderNode(node->left); // 左visitTreeNode(node); // 根inOrderNode(node->right); // 右}
}
void inOrderBTree(const BinaryTree* tree) {inOrderNode(tree->root);printf("\n");
}
// --- 后序遍历 ---
static void postOrderNode(const TreeNode *node) {if (node) {postOrderNode(node->left);postOrderNode(node->right);visitTreeNode(node);}
}
void postOrderBTree(const BinaryTree* tree)
{postOrderNode(tree->root);printf("\n");
}6.基于队列的广度优先遍历
/* 广度遍历* 1.引入一个任务队列,先把根节点入队* 2.从任务队列中,取出一个节点,处理他(访问)* 3.如果2步的节点,有左那么左就入队,有右那么右就入队* 4.重复第2步*/
void levelOrderBTree(const BinaryTree* tree) {// 1.申请一个任务队列,用顺序存储,循环队列,队列里每个元素应该是节点的地址
#define MaxQueueSize 8TreeNode* queue[MaxQueueSize];int front, rear;front = rear =0;// 2.根节点入队queue[rear] = tree->root;rear = (rear + 1) % MaxQueueSize;// 3.开始循环系统处理事务while (front != rear) {// 3.1 出队并访问TreeNode* node = queue[front];front = (front + 1) % MaxQueueSize;visitTreeNode(node);// 3.2 左右孩子(新任务)入队if (node->left) {queue[rear] = node->left;rear = (rear + 1) % MaxQueueSize;}if (node->right) {queue[rear] = node->right;rear = (rear + 1) % MaxQueueSize;}}
}
7.测试函数
#include "binaryTree.h"
#include <stdio.h>BinaryTree *initTree()
{TreeNode* nodeA = createTreeNode('A');TreeNode* nodeB = createTreeNode('B');TreeNode* nodeC = createTreeNode('C');TreeNode* nodeD = createTreeNode('D');TreeNode* nodeE = createTreeNode('E');TreeNode* nodeF = createTreeNode('F');TreeNode* nodeG = createTreeNode('G');TreeNode* nodeH = createTreeNode('H');TreeNode* nodeK = createTreeNode('K');BinaryTree* tree = createBinaryTree(nodeA);insertBinaryTree(tree,nodeA,nodeB,nodeE);insertBinaryTree(tree,nodeB,NULL,nodeC);insertBinaryTree(tree,nodeE,NULL,nodeF);insertBinaryTree(tree,nodeC,nodeD,NULL);insertBinaryTree(tree,nodeF,nodeG,NULL);insertBinaryTree(tree,nodeG,nodeH,nodeK);return tree;
}void test01()
{BinaryTree *tree = initTree();printf("tree count:%d\n", tree->count);printf("PreOrder traverse:");preOrderBTree(tree);printf("InOrder traverse:");inOrderBTree(tree);printf("PostOrder traverse:");postOrderBTree(tree);printf("LevelOrder traverse:");levelOrderBTree(tree);
}int main()
{test01();return 0;
}
结果为:

四、挑战极限:非递归的深度遍历
递归虽优雅,但在树的深度过大时,可能导致系统栈溢出。因此,掌握非递归的实现方式是专业程序员的必备技能。我们需要手动模拟递归的过程,而模拟递归的“调用栈”,我们使用的工具正是——栈。
1.非递归先序遍历
思路:用栈作为“待办事项”列表。为了保证“根->左->右”的顺序,弹栈时先处理根,入栈时要先压右孩子,再压左孩子。
/* 非递归实现先序遍历,基本思路:* 先序的结果是当前节点,再左节点,最后右节点,把栈当作任务的暂存空间,* 先压右节点,再压左节点,一旦弹栈,出现呢的是左节点,* 基本步骤:* 1. 初始化部分* 将根节点压栈* 2. 循环处理任务部分* 2.1 弹栈,访问弹出来的节点,判断节点有右先压右,有左再压左,保证先右后左* 2.2 循环出栈,直到栈内无元素*/void preOrderBtreeNoRecursion(const BinaryTree* tree) {ArrayStack stack;initArrayStack(&stack);pushArrayStack(&stack, tree->root);TreeNode* node;while (!isEmptyArrayStack(&stack)) {node = getTopArrayStack(&stack);popArrayStack(&stack);visitTreeNode(node);// 先压右,再压左,保证出栈时左先于右if (node->right) {pushArrayStack(&stack, node->right);}if (node->left) {pushArrayStack(&stack, node->left);}}
}
2. 非递归中序遍历
思路:这是三种非递归遍历中最具技巧性的。
- 用一个指针
node从根开始,一路将所有左孩子压入栈中,直到最左边的尽头。 - 此时,从栈中弹出一个节点,这个节点就是当前子树中“最左”的,访问它。
- 然后,将
node指针转向弹出节点的右孩子,重复步骤1。
/* 以根节点开始,整条左边进栈,从栈中弹出节点,开始访问* 如果这个节点有右孩子,把右孩子当作新节点* 再次整条边进栈,再弹栈*/
void inOrderBtreeNoRecursion(const BinaryTree* tree) {ArrayStack stack;initArrayStack(&stack);TreeNode *node = tree->root;while (stack.top > 0 || node) {if (node) {// 一路向左,全部压栈pushArrayStack(&stack, node);node = node->left;} else {// 左边到头,弹栈访问,转向右边node = getTopArrayStack(&stack);popArrayStack(&stack);visitTreeNode(node);node = node->right;}}
}
3.栈的内容
typedef void* TreeElement;
#define MaxStackSize 16typedef struct
{TreeElement data[MaxStackSize];int top;
} ArrayStack;// 递增空栈
void initArrayStack(ArrayStack *stack);void pushArrayStack(ArrayStack *stack, TreeElement e);
void popArrayStack(ArrayStack *stack);TreeElement getTopArrayStack(const ArrayStack *stack);int isEmptyArrayStack(const ArrayStack *stack);
int isFullArrayStack(const ArrayStack *stack);
#include <string.h>
#include "arrayStack.h"// 递增空栈
void initArrayStack(ArrayStack* stack)
{memset(stack->data, 0, sizeof(stack->data));stack->top = 0;
}void pushArrayStack(ArrayStack *stack, TreeElement e)
{stack->data[stack->top] = e;++stack->top;
}void popArrayStack(ArrayStack *stack)
{--stack->top;
}TreeElement getTopArrayStack(const ArrayStack *stack)
{int pos = stack->top - 1;return stack->data[pos];
}int isEmptyArrayStack(const ArrayStack *stack)
{return stack->top == 0;
}int isFullArrayStack(const ArrayStack *stack)
{return stack->top == MaxStackSize;
}
4.测试函数
void test02()
{BinaryTree *tree = initTree();printf("tree count:%d\n", tree->count);printf("NoRecursion PreOrder traverse:");preOrderBtreeNoRecursion(tree);printf("\n");printf("NoRecursion InOrder traverse:");inOrderBtreeNoRecursion(tree);
}int main()
{test02();return 0;
}
结果为:

五、总结:探索的蓝图
今天,我们掌握了遍历二叉树的两种核心思想和多种实现方法:
- 深度优先 (DFS):依赖递归或栈,深入探索分支,分为先序、中序、后序三种。
- 广度优先 (BFS):依赖队列,层层推进,是层次遍历的唯一方式。
这些遍历方法不仅仅是理论知识,它们是后续所有高级树操作(如查找、构建、修改)的基础蓝图。不掌握遍历,就无法真正地驾驭树。
我们已经学会了如何在树的世界里“行走”,接下来,我们将利用这些行走技巧,去探索一类具有特殊“秩序”的树——二叉搜索树,看看它如何实现高效的查找操作。
