别让链表兜圈子——力扣141.环形链表

力扣141.环形链表

---

一、题目简介

给你一个链表的头节点 head，判断该链表中是否存在环。
如果存在一个节点，可以通过连续跟踪 next 指针再次到达自身，那么说明链表存在环。

示例：

输入：head = [3,2,0,-4], pos = 1  
输出：true （尾部连接到第二个节点）

---

二、题意理解

我们可以把链表想象成一条公路：

• 如果有环，就意味着这条路是“封闭赛道”，你走一圈能回到起点；
• 如果没环，就是“单向直路”，你一直往前最终会到 null。

---

三、解法思路对比

方法	思想	时间复杂度	空间复杂度	是否推荐
方法一：哈希表记录访问过的节点	记录每个节点，看是否重复	O(n)	O(n)	简单易懂
方法二：快慢指针（Floyd判圈法）	一快一慢指针，若相遇则有环	O(n)	O(1)	高效且优雅
方法三：修改节点标记法（不推荐）	改变节点值来标记访问	O(n)	O(1)	会破坏原链表结构

---

四、思路详解

---

方法一：哈希表法（Set 判断重复节点）

思路：

1. 用一个 Set 存储访问过的节点；
2. 每遍历一个节点，就检查它是否已存在；
3. 若存在，说明成环；若遍历结束仍无重复，则无环。

代码实现：

class Solution {public boolean hasCycle(ListNode head) {Set<ListNode> visited = new HashSet<>();while (head != null) {if (visited.contains(head)) {return true;}visited.add(head);head = head.next;}return false;}
}

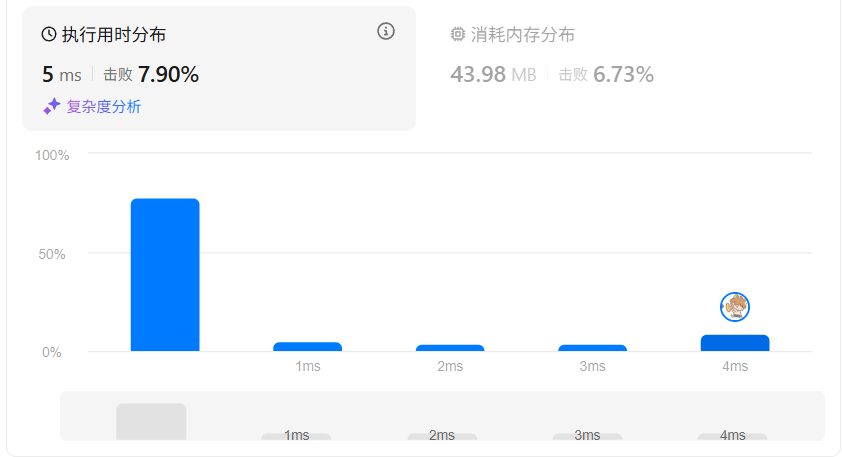
优点：思路直观、容易调试
缺点：需要额外 O(n) 空间

---

方法二：快慢指针（Floyd 判圈法）

这是最经典、最优雅的解法。

• 设置两个指针：slow 一次走一步，fast 一次走两步；
• 若链表无环，fast 会先到达 null；
• 若链表有环，fast 最终会在环内追上 slow。

代码实现：

class Solution {public boolean hasCycle(ListNode head) {if (head == null || head.next == null) return false;ListNode slow = head;ListNode fast = head.next;while (slow != fast) {if (fast == null || fast.next == null) return false;slow = slow.next;fast = fast.next.next;}return true;}
}

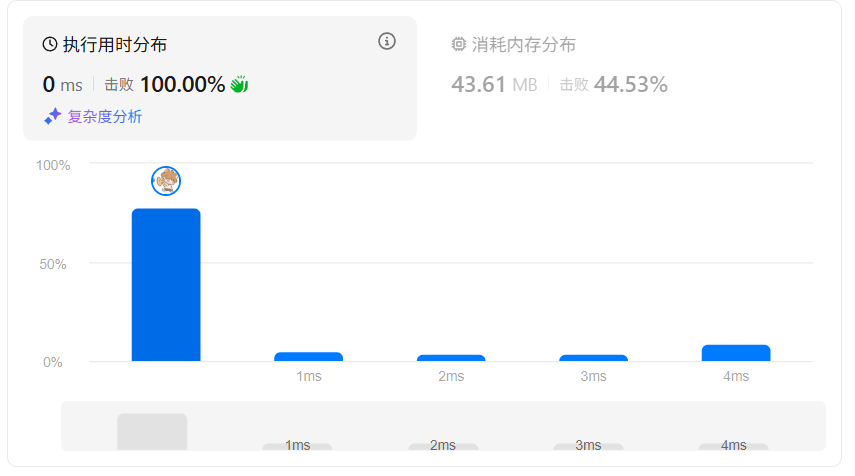
优点：时间 O(n)、空间 O(1)，是面试中的首选方案
缺点：理解上略有抽象，但掌握后非常高效

---

方法三：修改节点标记法（了解即可）

思路是通过修改节点值或设置特殊标志来标记访问过的节点，如果再次遇到相同标志则说明存在环。
但这种做法会破坏原链表数据结构，不推荐在实际开发或面试中使用。

---

五、总结对比

方法	思想	时间复杂度	空间复杂度	特点
哈希表法	记录访问节点	O(n)	O(n)	简单易懂
快慢指针法	龟兔赛跑	O(n)	O(1)	高效优雅
修改节点标记法	改值标记	O(n)	O(1)	破坏结构，不推荐

---

六、总结

判断链表中是否有环的关键，不在于是否兜圈，而在于能否发现自己正在兜圈。
面试或实际开发中，推荐使用快慢指针法，兼顾性能与优雅。

---