「机器学习笔记12」支持向量机(SVM)详解：从数学原理到Python实战

一、SVM核心思想：什么是支持向量机？

支持向量机（Support Vector Machine, SVM）是一种强大的监督学习算法，主要用于分类和回归问题。它的基本思想非常直观：找到一个最优的决策边界，使得这个边界到两类数据点的距离最大化。

1.1 直观理解

想象你在桌子上要分开一堆红豆和绿豆，SVM的目标不是随便画一条线，而是找到那条能让红豆和绿豆都离这条线最远的线。这样即使有新豆子掉下来，也能很大概率被正确分类。

支持向量就是离这条线最近的那些豆子，它们"支撑"着这条分界线，SVM的名字也由此而来。

1.2 基本概念

• 超平面：在N维空间中的决策边界（二维中是线，三维中是平面）
• 间隔：决策边界到最近数据点的距离
• 支持向量：距离决策边界最近的数据点，决定边界的位置

二、数学原理：SVM的公式推导

2.1 线性可分与最大间隔

对于线性可分数据，SVM的目标是找到一个超平面： $$w^{T}x+b=0$$ 其中 $w$ 是法向量（决定方向），$b$ 是位移项（决定位置）。

样本点 $x_i$ 到超平面的距离为： $$r=\frac{|w^T{x}_i+b|}{\Vert w\Vert }$$

SVM的优化目标是最大化间隔，即： $$\underset{w,b}{\max }\frac{2}{\Vert w\Vert }\text{s.t.}{y}_i(w^T{x}_i+b)\ge 1,i=1,2,\dots ,m$$

为方便求解，通常转化为等价问题： $$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2\text{s.t.}{y}_i(w^T{x}_i+b)\ge 1,i=1,2,\dots ,m$$

2.2 拉格朗日对偶问题

使用拉格朗日乘子法将约束问题转化为无约束问题。拉格朗日函数为： $$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(1-y_i(w^T{x}_i+b)\right)$$

通过对 $w$ 和 $b$ 求偏导并令其为0，得到对偶问题： $$\underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$ $$\text{s.t.}\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\dots ,m$$

2.3 支持向量的重要性

从KKT条件可知，只有那些 ${\alpha }_i>0$ 对应的样本点才是支持向量。最终的分类决策函数只依赖于这些支持向量： $$f(x)=\text{sign}\left(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^{T}x+b\right)$$

这种稀疏性使得SVM在预测时非常高效。

三、处理线性不可分：软间隔与核技巧

3.1 软间隔SVM

现实中的数据往往不是完美线性可分的。SVM通过软间隔技术允许一些样本违反约束条件。

引入松弛变量 ${\xi }_i\ge 0$，优化问题变为： $$\underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m{\xi }_i$$ $$\text{s.t.}{y}_i(w^T{x}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0$$

其中 $C>0$ 是惩罚参数，控制对误分类的容忍度：

• $C$ 值越大，对错误惩罚越大，间隔越窄，可能过拟合
• $C$ 值越小，对错误容忍度越高，间隔越宽，可能欠拟合

3.2 核技巧：非线性SVM的利器

对于非线性问题，SVM使用核技巧将数据映射到高维空间。核函数定义为： $$K(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$$

常用核函数包括：

1. 线性核：$K(x_i,x_j)=x_i^T{x}_j$
2. 多项式核：$K(x_i,x_j)=(x_i^T{x}_j+c{)}^d$
3. 高斯核（RBF）：$K(x_i,x_j)=\exp (-\gamma \Vert x_i-x_j{\Vert }^2)$
4. Sigmoid核：$K(x_i,x_j)=\tanh (\gamma x_i^T{x}_j+r)$

表：不同核函数的比较

核函数	适用场景	优点	缺点
线性核	线性可分、特征维度高	计算简单、可解释性强	不能处理非线性问题
多项式核	有一定规律的非线性	可控制复杂度	参数多、计算复杂度高
高斯核	复杂的非线性问题	适用性广、效果好	参数选择敏感、可解释性差
Sigmoid核	特定分类问题	类似神经网络	不一定满足Mercer条件

四、Python实战：从零实现SVM

4.1 使用Scikit-learn实现SVM分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, confusion_matrix# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 只使用前两个特征便于可视化
y = iris.target# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42
)# 创建SVM分类器（使用RBF核）
svm_model = SVC(kernel='rbf', C=1.0, gamma='scale')
svm_model.fit(X_train, y_train)# 预测测试集
y_pred = svm_model.predict(X_test)# 评估模型性能
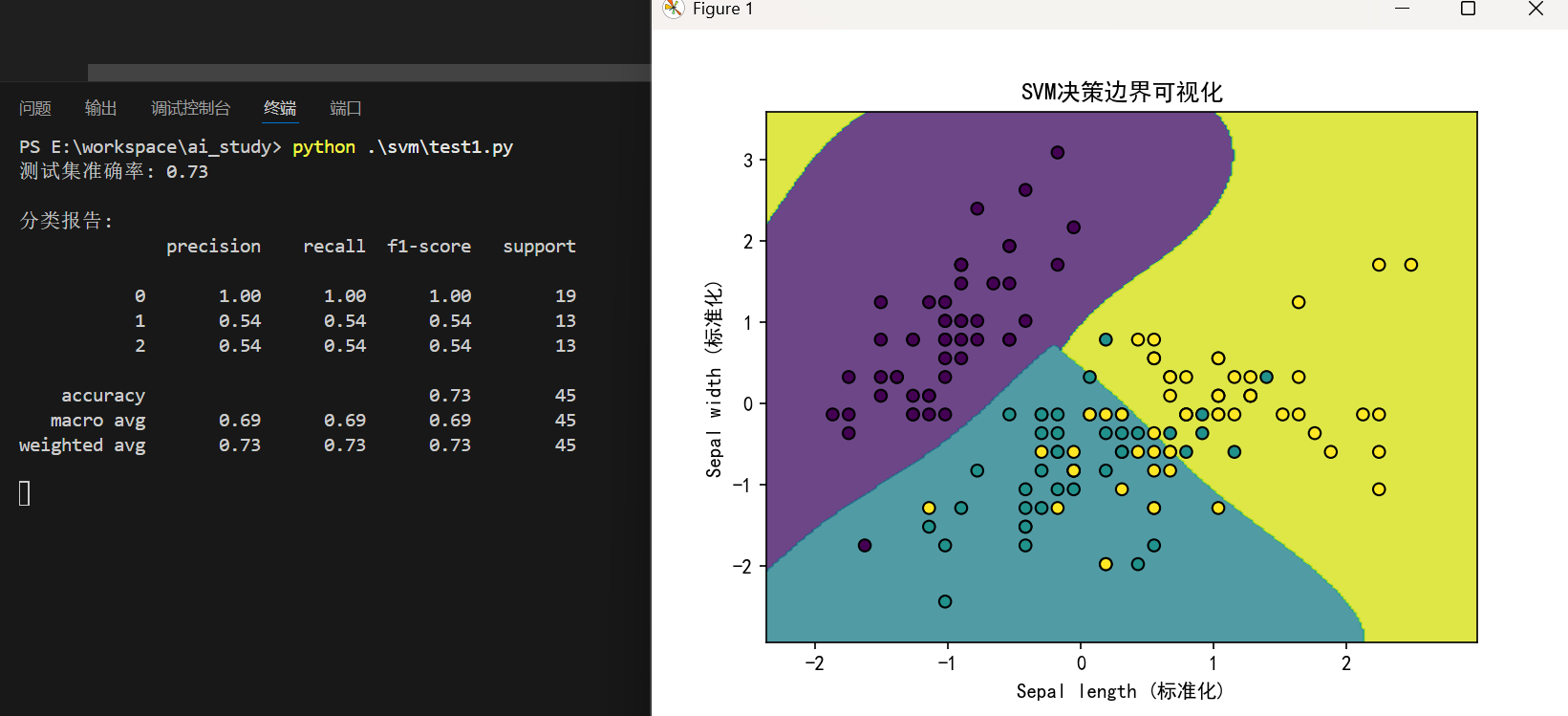
print("测试集准确率: {:.2f}".format(svm_model.score(X_test, y_test)))
print("\n分类报告:")
print(classification_report(y_test, y_pred))# 可视化决策边界
def plot_decision_boundary(model, X, y):x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.8)plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')plt.xlabel('Sepal length (标准化)')plt.ylabel('Sepal width (标准化)')plt.title('SVM决策边界可视化')plt.show()plot_decision_boundary(svm_model, X_scaled, y)

执行结果:

4.2 多核函数比较实验

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
import pandas as pd# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 只使用前两个特征便于可视化
y = iris.target# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42
)# 不同核函数的SVM比较
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
results = []for kernel in kernels:if kernel == 'poly':model = SVC(kernel=kernel, degree=3, C=1.0)else:model = SVC(kernel=kernel, C=1.0)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)results.append({'Kernel': kernel,'Accuracy': accuracy,'Support Vectors': len(model.support_vectors_)})results_df = pd.DataFrame(results)
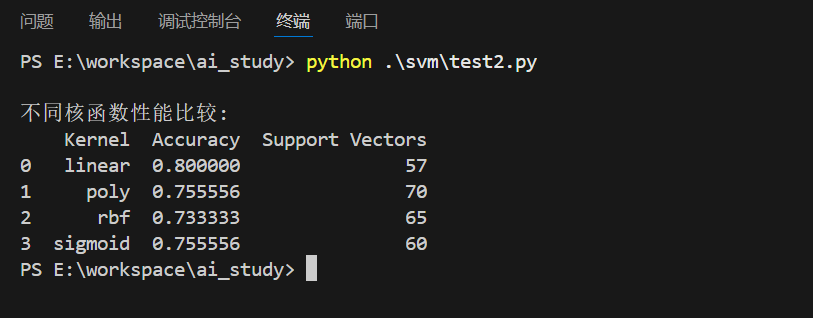
print("\n不同核函数性能比较:")
print(results_df)

运算结果:

4.3 参数调优实战

from sklearn.model_selection import GridSearchCV
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 只使用前两个特征便于可视化
y = iris.target# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)  # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42
)# 定义参数网格
param_grid = [{'C': [0.1, 1, 10, 100], 'kernel': ['linear']},{'C': [0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1], 'kernel': ['rbf']},{'C': [0.1, 1, 10, 100], 'degree': [2, 3, 4], 'kernel': ['poly']}
]# 网格搜索
grid_search = GridSearchCV(SVC(), param_grid, cv=5, scoring='accuracy', n_jobs=-1
)
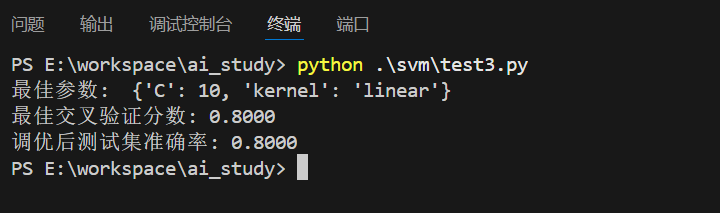
grid_search.fit(X_train, y_train)print("最佳参数: ", grid_search.best_params_)
print("最佳交叉验证分数: {:.4f}".format(grid_search.best_score_))# 使用最佳参数训练最终模型
best_svm = grid_search.best_estimator_
y_pred_best = best_svm.predict(X_test)
best_accuracy = accuracy_score(y_test, y_pred_best)
print("调优后测试集准确率: {:.4f}".format(best_accuracy))

执行结果:

五、SVM的优缺点与适用场景

5.1 优点

1. 高维有效：特征数远多于样本数时仍能良好工作
2. 小样本优势：适合训练数据不多的场景
3. 避免过拟合：最大化间隔原则增强泛化能力
4. 非线性处理：核技巧可解决复杂分类问题
5. 解的稀疏性：只需存储支持向量，预测效率高

5.2 缺点

1. 参数敏感：核函数和惩罚参数C的选择影响大
2. 大规模训练慢：样本数量大时训练耗时较长
3. 黑箱问题：使用核函数后模型可解释性变差
4. 概率估计：需要额外计算才能得到概率输出

5.3 适用场景

1. 文本分类：高维稀疏数据，SVM表现优异
2. 图像识别：如手写数字识别、人脸检测
3. 生物信息学：基因分类、蛋白质结构预测
4. 金融预测：股票趋势分析、信用评分

六、实践建议与技巧

6.1 数据预处理

SVM对特征尺度敏感，必须进行特征缩放：

from sklearn.preprocessing import StandardScalerscaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

6.2 参数选择策略

1. 先尝试线性核：如果效果不错，则计算简单、可解释性强
2. RBF核作为默认选择：适用于大多数非线性问题
3. C值选择：通常从 $[0.1,1,10,100]$ 中通过交叉验证选择
4. γ值选择：RBF核的γ参数控制模型复杂度，常用’scale’或’auto’

6.3 处理大规模数据

当数据量很大时（>10万样本），考虑：

• 使用线性SVM（LinearSVC）
• 采用随机梯度下降求解
• 使用近似算法或采样方法

七、总结

支持向量机通过最大化分类间隔和核技巧，提供了强大的分类能力。理解其数学原理有助于在实际应用中更好地选择模型参数和核函数。

关键要点：

1. SVM的核心是最大化间隔，提高泛化能力
2. 支持向量决定了决策边界的位置
3. 软间隔技术处理噪声和异常点
4. 核技巧优雅地解决非线性问题
5. 参数调优对SVM性能至关重要

SVM作为机器学习经典算法，虽然后来有深度学习等新技术出现，但其思想精髓仍值得深入学习和掌握。希望本文能帮助你全面理解SVM并在实际项目中成功应用。